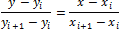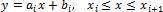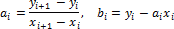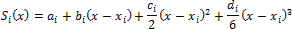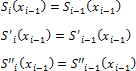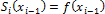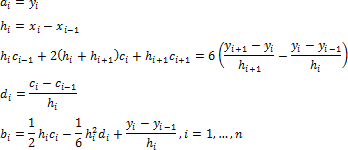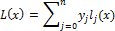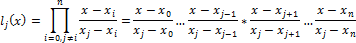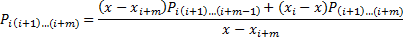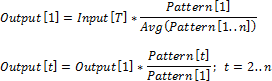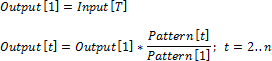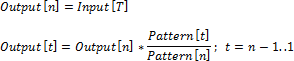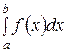Что называется задачей интерполяции
Интерполяция
Интерполяция использует значения некоторой функции, заданные в ряде точек, чтобы предсказать значения функции между ними. Перечисленные ниже методы предназначены для создания ряда с более высокой частотой наблюдений на основе ряда с низкой частотой. Например, вычислить ряд с квартальной динамикой на основе ряда годовых данных.
Линейная интерполяция
Геометрическая интерполяция
При геометрической интерполяции значения результирующей динамики пропорциональны значению инкремента и обратно пропорциональны фактору, вычисленному на основе инкремента. Инкремент экспоненциально зависит от логарифма относительного прироста исходной динамики, умноженного на длину периода результирующей динамики.
Рассмотрим принцип геометрического метода на примере вычисления квартальных данных на основе годовых.
X [ t ] – исходные данные по годам;
Factor [ t ] = (1 + Inc [ t ] + Inc [ t ]^2 + Inc [ t ]^3) / 4 – значение фактора;
Интерполяция для других динамик осуществляется аналогичным образом.
Интерполяция кубическими сплайнами
Сплайны позволяют эффективно решать задачи обработки экспериментальных зависимостей между параметрами, имеющих достаточно сложную структуру. Наиболее широкое практическое применение, в силу их простоты, нашли кубические сплайны. Основные идеи теории кубических сплайнов сформировались в результате попыток математически описать гибкие рейки из упругого материала (механические сплайны), которыми издавна пользовались чертежники в тех случаях, когда возникала необходимость проведения через заданные точки достаточно гладкой кривой. Известно, что рейка из упругого материала, закрепленная в некоторых точках и находящаяся в положении равновесия, принимает форму, при которой ее энергия является минимальной. Это фундаментальное свойство позволяет эффективно использовать сплайны при решении практических задач обработки экспериментальной информации.
функция S ( x ), а также ее первая и вторая производные непрерывны на отрезке [a, b];
Условие непрерывности всех производных до второго порядка записываются в виде:
Если функция f ( x ) является полиномом третьей или меньше степени, данные воспроизводятся более точно, если граничные условия сплайна c 0 и c n равны точным значениям второй производной кубического полинома.
Интерполяция многочленом Лагранжа
Лагранж предложил методику вычисления подобных многочленов:
Где базисные полиномы определяются по следующей формуле:
l j ( x ) обладают свойствами:
являются многочленами степени n ;
Полиноминальная интерполяция
Полиномиальная интерполяция является наиболее известным из методов одномерной интерполяции. Её достоинствами являются простота реализации и хорошее качество получаемых интерполянтов.
Равномерная интерполяция
Значение исходного ряда делится на число наблюдений, попадающих в один период результирующего ряда. Полученное значение присваивается всем наблюдениям нового ряда, в пределах одного периода.
Повторная интерполяция
Значения исходного ряда повторяются на всех наблюдениях ряда с более высокой частотой динамики.
Интерполяция по шаблону
Рассмотрим три метода интерполяции по шаблону:
среднее по элементам
по первому элементу
по последнему элементу
Первое значение
Значение первой точки результирующей динамики будет совпадать со значением точки на исходной динамике. Значения в остальных точках результирующей динамики остаются пустыми.
Последнее значение
Значение последней точки результирующей динамики будет совпадать со значением точки на исходной динамике. Значения в остальных точках результирующей динамики остаются пустыми.
Интерполяция
Интерполя́ция, интерполи́рование — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
Многим из тех, кто сталкивается с научными и инженерными расчётами часто приходится оперировать наборами значений, полученных опытным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называется аппроксимацией. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.
Существует также близкая к интерполяции задача, которая заключается в аппроксимации какой-либо сложной функции другой, более простой функцией. Если некоторая функция слишком сложна для производительных вычислений, можно попытаться вычислить её значение в нескольких точках, а по ним построить, то есть интерполировать, более простую функцию. Разумеется, использование упрощенной функции не позволяет получить такие же точные результаты, какие давала бы первоначальная функция. Но в некоторых классах задач достигнутый выигрыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах.
Следует также упомянуть и совершенно другую разновидность математической интерполяции, известную под названием «интерполяция операторов». К классическим работам по интерполяции операторов относятся теорема Рисса-Торина (Riesz-Thorin theorem) и теорема Марцинкевича (Marcinkiewicz theorem), являющиеся основой для множества других работ.
Содержание
Определения
Рассмотрим систему несовпадающих точек 



Задача интерполяции состоит в поиске такой функции 
Пример
1. Пусть мы имеем табличную функцию, наподобие описанной ниже, которая для нескольких значений 

 |  |
|---|---|
| 0 | 0 |
| 1 | 0,8415 |
| 2 | 0,9093 |
| 3 | 0,1411 |
| 4 | −0,7568 |
| 5 | −0,9589 |
| 6 | −0,2794 |
Интерполяция помогает нам узнать какое значение может иметь такая функция в точке, отличной от указанных (например, при x = 2,5).
К настоящему времени существует множество различных способов интерполяции. Выбор наиболее подходящего алгоритма зависит от ответов на вопросы: как точен выбираемый метод, каковы затраты на его использование, насколько гладкой является интерполяционная функция, какого количества точек данных она требует и т. п.
2. Найти промежуточное значение (способом линейной интерполяции).
| 6000 | 15.5 |
| 6378 | ? |
| 8000 | 19.2 |
Способы интерполяции
Интерполяция методом ближайшего соседа
Простейшим способом интерполяции является интерполяция методом ближайшего соседа.
Интерполяция многочленами
На практике чаще всего применяют интерполяцию многочленами. Это связано прежде всего с тем, что многочлены легко вычислять, легко аналитически находить их производные и множество многочленов плотно в пространстве непрерывных функций (теорема Вейерштрасса).
Обратное интерполирование (вычисление x при заданном y)
Интерполяция функции нескольких переменных
Другие способы интерполяции
Смежные концепции
См. также
Полезное
Смотреть что такое «Интерполяция» в других словарях:
ИНТЕРПОЛЯЦИЯ — 1) способ определять по ряду данных величин какого либо математического выражения промежуточные его величины; так напр., по дальности полета ядра при угле возвышения оси пушечного канала в 1°, 2°, 3°, 4° и т. д. можно определить помощью… … Словарь иностранных слов русского языка
интерполяция — вставка, интерполирование, включение, отыскание Словарь русских синонимов. интерполяция см. вставка Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Александрова. 2 … Словарь синонимов
интерполяция — Вычисление промежуточных значений между двумя известными точками. Например: linear линейная интерполяция exponential экспоненциальная интерполяция Процесс вывода цветного изображения, когда пикселы, относящиеся к области между двумя цветными… … Справочник технического переводчика
Интерполяция — (interpolation) Оценка значения неизвестной величины, находящейся между двумя точками ряда известных величин. Например, зная показатели населения страны, полученные при проведения переписи населения, проводившейся с интервалом в 10 лет, можно… … Словарь бизнес-терминов
Интерполяция — с латинского собственно «подделка». Так называются ошибочные поправки или позднейшие вставки в рукописях, сделанные переписчиками или читателями. Особенно часто этот термин употребляется в критике рукописей античных писателей. В этих рукописях… … Литературная энциклопедия
Интерполяция — нахождение промежуточных значений некоторой закономерности (функции) по ряду известных ее значений. По английски: Interpolation См. также: Преобразования данных Финансовый словарь Финам … Финансовый словарь
интерполяция — и, ж. interpolation f. < лат. interpolatio изменение; переделка, искажение. 1. Вставка позднейшего происхождения в каком л. тексте, не принадлежащая оригиналу. БАС 1. В древних рукописях много интерполяций, внесенных переписчиками. Уш. 1934. 2 … Исторический словарь галлицизмов русского языка
ИНТЕРПОЛЯЦИЯ — (interpolatio), пополнение эмпйрич. ряда значений какой либо величины недостающими промежуточными значениями ее. Интерполирование может быть произведено тремя способами: математич., графич. и логическим. В основе их лежит общая им гипотеза о том … Большая медицинская энциклопедия
ИНТЕРПОЛЯЦИЯ — (от латинского interpolatio изменение, переделка), отыскание промежуточных значений величины по некоторым известным ее значениям. Например, отыскание значений функции y = f(x) в точках x, лежащих между точками x0 и xn, x0 … Современная энциклопедия
ИНТЕРПОЛЯЦИЯ — в филологии изменение первоначального текста; вставка переписчиком или переводчиком в текст слов или фраз, отсутствовавших в оригинале … Большой Энциклопедический словарь
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Интерполяция
Интерполяция или интерполирование — приближенное или точное нахождение какой-либо величины по известным отдельным значениям этой же величины, или других величин, с ней связанных.
Происхождение слова «интерполяция» ☞ ЗДЕСЬ.
Задача интерполяции решается в разных классах функций — полиномов алгебраических или тригонометрических, комбинаций экспонент; в классе рациональных функций. Начинаем изложение материала с самого простого случая —
Полиномиальная интерполяция
Все множество интерполяционных полиномов, принимающих значения по таблице, можно представить в виде
Решение ☞ ЗДЕСЬ.
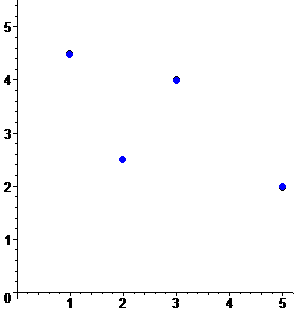
Пусть имеется интерполяционная таблица
Пример. Интерполяционный полином для таблицы
Следовательно, применение вычислительных методов решения систем линейных уравнений — типа метода Гаусса — к системе с матрицей Вандермонда столкнется с необходимостью строгого контроля округлений. ♦
Практическое построение интерполяционного полинома производится альтернативными алгоритмами — посредством вспомогательных промежуточных представлений полинома в специальных, сравнительно просто вычисляемых, видах. Самыми распространенными являются формы Лагранжа и Ньютона.
Интерполяционый полином в форме Лагранжа
Пример. Построить интерполяционный полином по таблице
Рекурсивное вычисление коэффициентов
В настоящем пункте мы произведем «доводку» метода Лагранжа до коэффициентов интерполяционного полинома
Интерполяционный полином в форме Ньютона
Основной недостаток построения интерполяционного полинома по методу (в форме) Лагранжа заключается в том, что при добавлении в таблицу нового узла (новых результатов измерений), в формуле приходится пересчитывать все слагаемые. От этого недостатка свободен метод Ньютона, в котором добавление нового узла ведет к добавлению лишь одного слагаемого к построенному ранее полиному.
Теорема. Интерполяционный полином в форме Ньютона записывается в виде:
Применение полиномиальной интерполяции в задаче о разделении секрета
Обратная интерполяция
В одном из предшествующих ☝ пунктов решалcя следующий
Пример. Найти корни интерполяционного полинома, заданного таблицей
Интерполяционный полином Эрмита
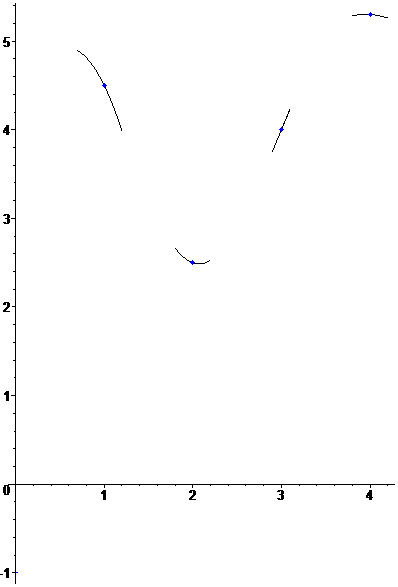
Пример. Построить интерполяционный полином по таблице
Построить уравнение «горки»: найти полином из условий
Следующий результат не очень связан с содержанием настоящего пункта, но надо было куда-то поместить.
Рациональная интерполяция
Первое решение задачи было предложено Коши в 1821 г. [9].
Теорема [Коши]. Обозначим:
Биографические заметки о Коши ☞ ЗДЕСЬ.
Другие примеры на применение теоремы Коши ☞ ЗДЕСЬ
Теорема Коши дает решение задачи в смысле «как правило». Дело в том, что задача рациональной интерполяции (в указанной постановке) не всегда разрешима.
Пример. Для таблицы
Альтернативный подход к решению задачи основывается на следующей теореме, развивающей результат К.Якоби [10,11]; он основан на идее из пункта ☝ о рекурсивном вычислении коэффициентов интерполяционного полинома.
Подробнее о методе Якоби (в том числе и об эффективном способе вычисления ганкелевых полиномов) ☞ ЗДЕСЬ.
Тригонометрическая интерполяция
Доказательство тривиально, если обратить внимание на аналогию с интерполяционным полиномом в форме Лагранжа. ♦
Теорема. Функция
Задача. Найти явные выражения для коэффициентов тригонометрического полинома из последней теоремы.
«Лобовое» решение аналогично решению задачи полиномиальной интерполяции — сведением ее к подходящей системе линейных уравнений.
Пример. Построить интерполяционный полином второго порядка по следующей таблице
Решение ☞ ЗДЕСЬ.
Для случая системы равноотстоящих узлов решение задачи значительно упрощается.
Подробное изложение теории тригонометрической интерполяции (и дискретного преобразования Фурье) ☞ ЗДЕСЬ
Интерполяция суммами экспонент
Материал настоящего пункта — сильная «выжимка» из [2]. Числовой пример — мой.
В отличие от рассмотренных выше задач алгебраической или тригонометрической интерполяции, поставленная задача является, во-первых, принципиально нелинейной относительно параметров, и, во-вторых, не всегда разрешимой.
Пример. Построить экспоненциальную функцию вида
Аппроксимация
Задача интерполяции является частным случаем более общей задачи аппроксимации функций, т.е. замены одной неизвестной или сложной для вычисления функции другой, более простой. Здесь существенно понятие «близости» функций, которое может быть различным в конкретных задачах.
Аппроксимация в случае недостоверности данных
Предположим теперь, что данные исходной таблицы не являются достоверными: значения обеих переменных подвержены воздействию случайных погрешностей одинакового порядка. Как воспользоваться этими данными для задачи аппроксимации? Мы рассмотрим здесь только две подобные задачи.
Координаты точки, для которой величина
Теорема 2 [3],[4]. Обозначим
$$ \begin
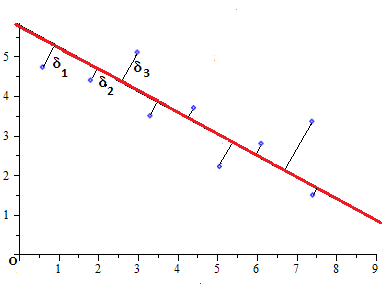
Метод наименьших квадратов
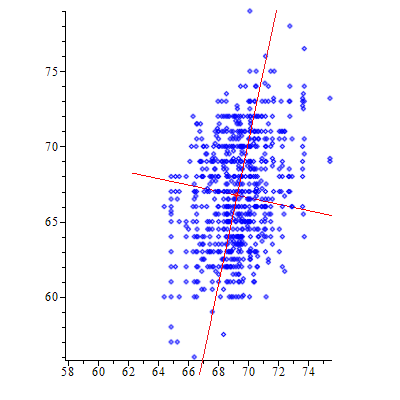
Пример. По методу наименьших квадратов построить уравнение прямой, аппроксимирующей множество точек плоскости, заданных координатами из таблицы
$$ \begin
Дальнейшее развитие идеологии МНК ☞ ЗДЕСЬ.
Многомерная интерполяция
Сложности: парадокс Крамера
Прямоугольная сетка
Задачи
Источники
[1]. Mycielski J. Polynomials with Preassigned Values at their Branching Points. The American Mathematical Monthly, 77 (8).1970, pp. 853-855
[2]. Henrici P. Applied and Computational Complex Analysis. V. 1. 1974. NY. Wiley
[4]. Hilbert D. Ein Beitrag zur Theorie des Legendreschen Polynoms. Acta Math. Bd.18, 1894, S.155-160
[5]. Форсайт Дж., Молер К. Численное решение систем линейных алгебраических уравнений. М. Мир. 1969
[6]. Линник Ю.В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. М.ГИФМЛ. 1958
[7]. Калинина Е.А., Утешев А.Ю. Теория исключения. Учеб. пособие. СПб.: НИИ Химии СПбГУ, 2002. 72 с.
[8]. Утешев А.Ю., Тамасян Г.Ш. К задаче полиномиального интерполирования с кратными узлами. Вестник СПбГУ. Серия 10. 2010. Вып. 3, С. 76-85. Текст (pdf) ☞ ЗДЕСЬ
[9]. Cauchy A.-L. Cours d’Analyse de l’École Royale Polytechnique: Part I: Analyse Algébrique. Paris, France: L’Imprimerie Royale, 1821, pt. 1.
[10]. Jacobi C.G.J. Űber die Darstellung einer Reihe gegebner Werthe durch eine gebrochne rationale Function. J.reine angew. Math. 1846. Bd. 30, S. 127-156
[11]. Утешев А.Ю., Боровой И.И. Решение задачи рациональной интерполяции с использованием ганкелевых полиномов. Вестник СПбГУ. Серия 10. 2016. Вып. 4, С. 31-43. Текст ☞ ЗДЕСЬ (pdf).
[12]. Pearson K. On lines and planes of closest fit to systems of points in space. Phil. Mag. 1901. V.2, pp. 559-572
Постановка задачи интерполяции
Лекция 8
ОБРАБОТКА ДАННЫХ. ЧИСЛЕННЫЕ МЕТОДЫ ПРИБЛИЖЕНИЯ ФУНКЦИЙ. ИНТЕРПОЛЯЦИЯ
Содержание
· Области применения задачи приближения функций.
· Основные виды обработки данных: интерполяция, экстраполяция и аппроксимация.
· Постановка задачи интерполяции.
· Метод неопределенных коэффициентов
· Интерполяционный полином Лагранжа.
· Интерполяционный полином Ньютона.
· Погрешность полиномиальной интерполяции.
8.1. Области применения задачи приближения функций
В технологии обработки данных важное место занимают методы приближения функций более простыми, хорошо изученными функциями, методы численного дифференцирования и численного интегрирования. При этом исследуемая приближаемая функция может быть задана как в аналитическом, так и дискретном виде (в виде таблицы экспериментальных данных).
Подобные задачи (иначе интерполяция или аппроксимация функций) возникают в тех случаях, когда:
· функция задана в виде таблицы, и необходимо знать значения функции для промежуточных значений аргументов, расположенных в таблице между узлами xi, i = 0,…. n, а также для аргументов, расположенных вне таблицы;
· известно лишь табличное представление функции и требуется определить ее аналитическое выражение;
· известно аналитическое выражение функции, но оно имеет очень сложный вид, вследствие чего возникает необходимость представления этой функции в более простом виде. Например, при вычислении определенных интегралов вида
можно заменить подынтегральную функцию f(x) некоторой приближенной функцией P(x) в виде многочлена. Тогда
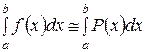
8.2. Основные виды обработки данных: интерполяция, экстраполяция и аппроксимация
Разберемся с рядом терминов, используемых в литературе при описании технологии приближения функций. Итак, пусть некоторая функция f(x)определена рядом своих узловых точек (xi, yi) на некотором отрезке [a, b]. Под интерполяцией мы будем подразумевать вычисление значений f(x) в любом промежутке [xi, xi+1] в пределах отрезка [a, b]. Соответственно, любое вычислениеf(x)вне отрезка [a, b] является экстраполяцией.
Наиболее распространены следующие виды интерполяции:
· линейная интерполяция, при которой промежуточные точки, расположенные между двумя узловыми точками (xi, yi) и (xi+1, yi+1), лежат на отрезке прямой, соединяющей две ближайшие узловые точки;
· квадратичная интерполяция, при которой промежуточные точки между узловыми точками (xi, yi), (xi+1, yi+1) и (xi+2, yi+2) лежат на отрезке параболы, соединяющей эти узловые точки;
· полиномиальная интерполяция, при которой промежуточные точки вычисляются как значение некоторого многочлена pn(x), имеющего значения в узловых точках точно совпадающие с fi(xi);
· сплайновая интерполяция, при которой промежуточные точки находятся с помощью отрезков полиномов невысокой степени, проходящих через узловые точки и поддерживающие определенные условия стыковки в концевых точках;
Подчеркнем ещё раз, что при интерполяции задача сводится к вычислению значений функции между узловыми точками (узлами), в то время как при экстраполяции — к вычислению функции вне того интервала, на котором она задана в виде таблицы, графически или иным способом.
При аппроксимации таблично заданная функция (что, кстати, не является обязательным признаком аппроксимации) заменяется другой функцией, как правило, более простой и поэтому более быстро вычисляемой. Последняя приближенно описывает поведение исходной функции на некотором отрезке. При этом на различных отрезках аппроксимирующие функции могут быть (и чаще всего бывают) разными.
Примечание. Для иллюстрации возможного использования процедуры аппроксимации можно привести задачу экстракции параметров моделей микроэлектронных приборов из экспериментальных данных.
Постановка задачи интерполяции
Пусть на отрезке xÎ[a, b] задана функция f(x), с помощью которой построена сеточная функция (табл. 8.1) или задана экспериментальная таблица (табл. 8.1).
Требуется найти аналитическое выражение функции F(x), совпадающей в узлах интерполяции со значениями данной функции, т.е.
Определение 2.Процесс вычисления значений функции F(x) в точках отличных от узлов интерполирования называется интерполированием функции f(x). Если xÎ[x0, xn], то задача вычисления приближенного значения функции в точке х называется интерполированием, иначе — экстраполированием.
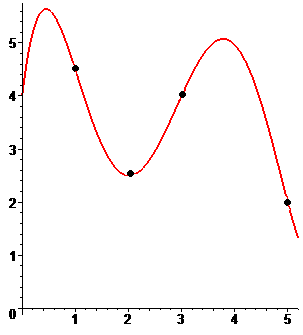
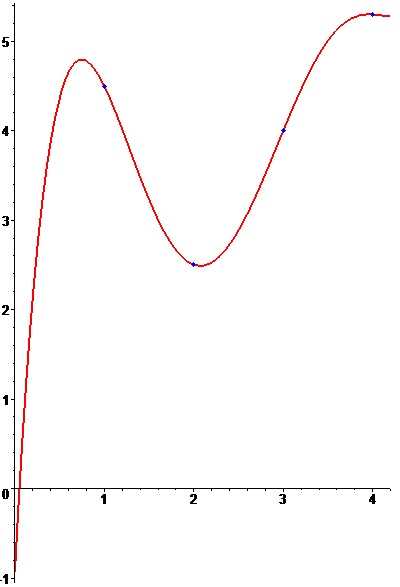
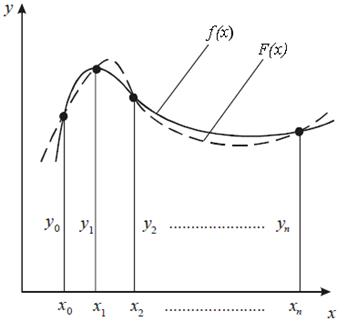
Геометрически задача интерполирования функции одной переменной означает построение кривой, проходящей через заданные точки (x0, y0), (x1, y1), …, (xn, yn) (рис. 8.1).
8.3.1. Метод неопределенных коэффициентов
В рассмотренной постановке задача может иметь бесконечное число решений или не иметь ни одного решения. Однако эта задача становится однозначно разрешимой, если вместо произвольной функции F(x) искать полином Pn(x)
степени не выше n, удовлетворяющий условиям (8.5), т. е. такой, что в каждой узловой точке i выполняется условие:
При сглаживании функции (или экспериментальной таблицы) с помощью интерполяции в соответствии с условием интерполяции (8.2) значение интерполирующей функции и значение заданной функции в узлах сетки должны быть одинаковыми, следовательно, погрешность интерполяции в узлах xi, i = 0,…, n равна нулю (рис. 8.1).
Рис. 8.1. Иллюстрация процедуры интерполяции
В общем случае задача интерполяции имеет не единственное решение, но в случае использования в качестве интерполирующей функции многочлена n-й степени (требующий n+1 узел интерполяции) задача интерполяция табличной функции вида (8.1) имеет единственное решение, т.е. коэффициенты a0,…, an (в количестве n+1) определяются единственным образом.
Действительно, используя табл. 8.1, можно составить систему из n+1 линейных уравнений (СЛАУ) относительно неизвестных коэффициентов a0,…, an:
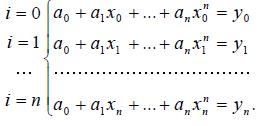
Матрица коэффициентов этой СЛАУ (8.6) носит специальное название — матрицы Вандермонда. Ее определитель не равен нулю, поскольку все значения узлов интерполяции различны между собой и ни одна из строк не является линейной комбинацией других строк, т.е.
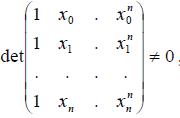
Примечание. Отметим, что вычисление коэффициентов полинома посредством решения системы (8.6) в вычислительной практике реализуется крайне редко. Причиной этого является плохая обусловленность матрицы Вандермонда, приводящая к заметному росту погрешности при выполнении условий интерполирования уже при сравнительно невысоких порядках полинома. К этому следует добавить, что вычислительные затраты реализации метода пропорциональны n 3 .
Дата добавления: 2016-04-22 ; просмотров: 5129 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ