Что называется временем релаксации и как оно связано с коэффициентом затухания

Что называется временем релаксации и как оно связано с коэффициентом затухания

Найдем отношение значений амплитуды затухающих колебаний в моменты времени t и (рис. 3.1):

,

где β – коэффициент затухания.

Натуральный логарифм отношения амплитуд, следующих друг за другом через период Т, называется логарифмическим декрементом затухания χ:

;

.

Выясним физический смысл χ и β.

Время релаксации τ – время, в течение которого амплитуда А уменьшается в e раз.

отсюда

Следовательно, коэффициент затухания β есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз.

Пусть N число колебаний, после которых амплитуда уменьшается в e раз. Тогда

; ;

.

Следовательно, логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз.

Если χ = 0,01, то N = 100.

При большом коэффициенте затухания происходит не только быстрое уменьшение амплитуды, но и заметно увеличивается период колебаний. Когда сопротивление становится равным критическому , а то круговая частота обращается в нуль ( ), а ( ), колебания прекращаются. Такой процесс называется апериодическим (рис. 3.2).

Отличия в следующем. При колебаниях тело, возвращающееся в положение равновесия, имеет запас кинетической энергии. В случае апериодического движения энергия тела при возвращении в положение равновесия оказывается израсходованной на преодоление сил сопротивления, трения.

Источник

Физика Б1.Б8.

Электронное учебное пособие по разделу курса физики Механика

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

Введение

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механическое движение – это изменение во времени взаимного расположения тел или частей одного и того же тела. Причиной, вызывающей механическое движение тела или его изменение, является воздействие со стороны других тел.

Развитие механики началось еще в древние времена, однако, как наука она формировалась в средние века. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564-1642) и английским ученым И. Ньютоном (1643-1727).

Механику Галилея-Ньютона принято называть классической механикой. В ней изучается движение макроскопических тел, скорости которых значительно меньше скорости света с в вакууме. Законы движения тел со скоростями, близкими к скорости света сформулированы А. Эйнштейном (1879-1955), они отличаются от законов классической механики. Теория Эйнштейна называется специальной теорией относительности и лежит в основе релятивистской механики. Законы классической механики неприемлемы к описанию движения микроскопических тел (элементарных частиц – электронов, протонов, нейтронов, атомных ядер, самих атомов и т.д.) их движение описывается законами квантовой механики.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

В механике для описания движения в зависимости от условий решаемой задачи пользуются различными упрощающими моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело, и т.д. Выбор той или иной модели диктуется необходимостью учесть в задаче все существенные особенности реального движения и отбросить несущественные, усложняющие решение.

Материальная точка – это тело обладающее массой, размеры и форма которого несущественны в данной задаче. Любое твердое тело или систему тел можно рассматривать как систему материальных точек. Для этого любое тело или тела системы нужно мысленно разбить на большое число частей так, чтобы размеры каждой части были пренебрежимо малы по сравнению с размерами самих тел.

Абсолютно твердое тело – это тело, расстояние между любыми точками которого остается неизменным в процессе движения или взаимодействия. Эта модель пригодна, когда можно пренебречь деформацией тел в процессе движения.

Абсолютно упругое и абсолютно неупругое тело – это два предельных случая реальных тел, деформациями которых можно и нельзя пренебречь в изучаемых процессах.

Любое движение рассматривается в пространстве и времени. В пространстве определяется местоположение тела, во времени происходит смена местоположений или состояний тела в пространстве, время выражает длительность состояния движения или процесса. Пространство и время –это два фундаментальных понятия, без которых теряется смысл понятия движения: движения не может быть вне времени и пространства.

Источник

Тема: ИССЛЕДОВАНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ С ПОМОЩЬЮ САМОПИСЦА

Знания, полученные при выполнении данной работы, потребуются при изучении механических колебаний в биологических системах и рассмотрении вопросов воздействия механических колебаний на человека на кафедрах физиологии, профессиональных болезней, медицины труда и др.

ЦЕЛЬ: изучить закономерности колебательных процессов на примере затухающих колебаний.

Для реализации цели необходимо:

а). Изучить литературу [1] по теме работы, раздел «Колебания».

б). Ответить на вопросы

1. Что называется колебанием?

2. Какие колебания называются затухающими?

3. Какой вид имеет уравнение затухающих колебаний?

4. Какой вид имеет закон движения затухающих колебаний?

5. Какому закону подчиняется изменение амплитуды затухающего колебания?

6. Какими величинами характеризуется затухание?

7. Что выражают логарифмический декремент затухания и коэффициент затухания?

8. Что называется временем релаксации и как оно связано с коэффициентом затухания?

ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ ИССЛЕДОВАНИЯ

Повторяющиеся во времени движения или изменения состояния называются колебаниями.

Примерами колебаний могут служить дыхательные движения грудной клетки, пульсации сосудистой стенки (пульс), суточные изменения температуры тела и др. Самым простым механическим колебанием является гармоническое колебание, при котором колеблющаяся величина (например, смещение) изменяется во времени по закону косинуса (или синуса):

x(t) – смещение от положения равновесия в данный момент времени;

A₀ – начальная амплитуда, т.е. максимальное смещение;

ω₀ – круговая частота собственных колебаний;

t – любой момент времени;

φ – начальная фаза (она может равняться нулю).

В реальных колебательных системах всегда существуют силы сопротивления, на преодоление которых затрачивается энергия колебательного движения, поэтому амплитуда колебаний свободно колеблющегося тела постепенно уменьшается, колебания затухают

Уравнение затухающего колебания имеет вид:

ω – круговая частота затухающих свободных колебани;

β – коэффициент затухания;

е – основание натурального логарифма, е=2,7183… ( ̴ 3)

Основными характеристиками затухающего колебания являются следующие величины:

β – коэффициент затухания, характеризующий быстроту убывания амплитуды в единицу времени, размерность [1/с];

N_e – число колебаний, за которое амплитуда уменьшилась в е раз,

ЗАДАНИЕ, ВЫПОЛНЯЕМОЕ В ЛАБОРАТОРИИ

Записать с помощью самописца графики затухающих колебаний маятника, определить коэффициент затухания, логарифмический декремент затухания, время релаксации и найти зависимость коэффициента затухания от массы маятника.

ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ИССЛЕДОВАНИЯ

Для проведения исследования используется экспериментальная установка, состоящая из колеблющегося тела – маятника и самописца. Маятник вручную выводится из положения равновесия, после освобождения он совершает затухающие колебания, а на ленте самописца записывается периодическая кривая с уменьшающейся амплитудой.

МЕТОДИКА ПРОВЕДЕНИЯ ИССЛЕДОВАНИЯ

1. Закрепить на штоке маятника груз массой 250 г. Установить скорость движения ленты самописца, нажав клавишу «5 мм/с». Включить самописец в сеть тумблером «сеть» и нажать клавишу «V». В течении 2 сек. Записать линию, соответствующую положению равновесия маятника (нулевую линию).

2. Отклонить рукой маятник от положения равновесия и отпустить. Наблюдать запись колебаний на ленте самописца до полного успокоения, прописать нулевую линию и выключить самописец. Пункты 1 и 2 повторить с грузами 500г и 1000г, получив, таким образом, 3 графика затухающих колебаний.

3. Отрезать ножницами ленту с графиками и обработать записи.

а) провести линейкой оси X и t, как показано на рис. 1.1.;

б) проградуировать ось t в секундах, т.е. найти сколько секунд k приходится на 1мм длины, взятой вдоль оси t: k= 1/V, где V – скорость движения ленты самописца в мм/с. Если V=5 мм/с, то k=1/5=0.2 (с/мм), значит, 1мм ленты соответствует 0.2 с;

в) найти период T колебаний в с, для чего расстояния между ближайшими точками одинаковых фаз колебаний умножить на k;

г) на каждом графике затухающих колебаний измерить 4 соседних амплитудных отклонения (А₁,А₂,А₃,А₄), относящихся друг от друга по времени на один период, как показано на рис. 1.1. Результаты занести в таблицу 1.1.

4. Рассчитать логарифмический декремент затухания для каждой пары амплитуд:

Вычислить коэффициент затухания: β=λ_ср/Т

Найти время релаксации по графику ῖ_r и расчетным путем: ῖ_р=1/β

Результаты вычислений занести в таблицу 1.1.

5. Сравнить вычисленное и найденной по графику значения времен релаксации.

6. Построить график зависимости коэффициента затухания от массы груза: β=f(m)

7. Сделать вывод о характере изменения коэффициента затухания при изменении массы маятника.

Закончив исследование, представить преподавателю отчет соответственно поставленной задаче, включающий результаты измерений и график с обоснованием их в виде вывода.

Источник

Время релаксации

Время релаксации — период времени, за который амплитудное значение возмущения в выведенной из равновесия физической системе уменьшается в e раз (e — основание натурального логарифма), в основном обозначается греческой буквой τ.

Согласно принципу Ле Шателье — Брауна при отклонении физической системы от состояния устойчивого равновесия возникают силы, которые пытаются вернуть систему к равновесному состоянию. Если в состоянии равновесия некоторая физическая величина f имеет значение , причём отклонение от равновесия , то в первом приближении можно считать, что эти силы пропорциональны отклонению. Кинетическое уравнение для величины f запишется в виде

,

где λ — некоторый параметр, а знак минус указывает на то, что реакция системы на возмущение приводит к возвращению к равновесному состоянию.

В таком случае величина f будет изменяться по закону:

,

где — начальное возмущение.

Использование

Приближение времени релаксации широко используется при описании кинетических процессов в физике, когда речь идет о кинетике установления равновесного состояния. Переход от неравновесного состояния к равновесию сопровождается диссипацией энергии и является необратимым процессом. Установление равновесия часто проходит в несколько этапов, которые характеризуются своими отдельными временами релаксации. Так, при возбуждении молекул светом установление теплового равновесия происходит за время порядка с, а вот люминесценция — излучение света возбуждёнными состояниями, может иметь характерные времена порядка наносекунд и даже микросекунд.

При описании многих физических процессов время релаксации берётся как феноменологический параметр, однако в отдельных случаях его можно определить через параметры микроскопических процессов, таких как вероятность квантовомеханического перехода или сечение рассеяния.

См. также

Полезное

Смотреть что такое «Время релаксации» в других словарях:

время релаксации — электрической поляризации; время релаксации Время, в течение которого поляризованность диэлектрика после снятия внешнего электрического поля уменьшается в e раз, где e основание натуральных логарифмов. Время, в течение которого отклонение системы … Политехнический терминологический толковый словарь

время релаксации — Время, в течение которого напряжения при релаксации уменьшаются в е раз (е = 2,718. ). [Сборник рекомендуемых терминов. Выпуск 82. Строительная механика. Академия наук СССР. Комитет научно технической терминологии. 1970 г.] Тематики… … Справочник технического переводчика

Время релаксации — – время, в течение которого напряжения при релаксации уменьшаются в е раз (е = 2,718….). [Строительная механика. Терминология. Выпуск 82. Изд. «Наука» М.1970] Рубрика термина: Теория и расчет конструкций Рубрики энциклопедии:… … Энциклопедия терминов, определений и пояснений строительных материалов

время релаксации — relaksacijos trukmė statusas T sritis chemija apibrėžtis Laikas, per kurį kurio nors dydžio nuokrypis nuo pusiausvirojo sumažėja e kartų. atitikmenys: angl. relaxation time rus. время релаксации; период релаксации … Chemijos terminų aiškinamasis žodynas

время релаксации — relaksacijos trukmė statusas T sritis fizika atitikmenys: angl. relaxation time vok. Erholungszeit, f; Relaxationszeit, f rus. время релаксации, n; период релаксации, m pranc. temps de relaxation, m … Fizikos terminų žodynas

ВРЕМЯ РЕЛАКСАЦИИ — – характерное время приближения системы к равновесному состоянию. В магнетизме – характеристика способности магнитных зерен или доменов в них менять направление намагниченности. Мелкие зерна магнитных минералов, время релаксации магнитных… … Палеомагнитология, петромагнитология и геология. Словарь-справочник.

время релаксации — relaksacijos trukmė statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, atvirkščiai proporcingas sistemos slopimo koeficientui, t. y. τ = 1/δ ; čia δ – slopimo koeficientas. atitikmenys: angl. relaxation time vok. Relaxationszeit,… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

время релаксации — relaksacijos trukmė statusas T sritis Standartizacija ir metrologija apibrėžtis Eksponentinio grįžimo į pusiausvyrą vyksmo trukmės konstanta. atitikmenys: angl. relaxation time vok. Relaxationszeit, f rus. время релаксации, n pranc. constante de… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

время релаксации — relaksacijos trukmė statusas T sritis Standartizacija ir metrologija apibrėžtis Laiko tarpas, per kurį tam tikro dydžio vertės nuokrypis nuo pradinės arba pusiausvirosios vertės sumažėja e (e = 2,71828…) kartų. atitikmenys: angl. relaxation time… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

Источник

Релаксация (Физика)

Релаксация (от лат. relaxatio — ослабление, уменьшение) — процесс установления термодинамического, а следовательно, и статистического равновесия в физической системе, состоящей из большого числа частиц.

Содержание

Свойства и виды

Релаксация — многоступенчатый процесс, так как не все физические параметры системы (распределение частиц по координатам и импульсам, температура, давление, концентрация в малых объёмах и во всей системе и другие) стремятся к равновесию с одинаковой скоростью. Обычно сначала устанавливается равновесие по какому-либо параметру (частичное равновесие), что также называется релаксацией. Все процессы релаксации являются неравновесными процессами, при которых в системе происходит диссипация энергии, то есть производится энтропия (в замкнутой системе энтропия возрастает). В различных системах релаксация имеет свои особенности, зависящие от характера взаимодействия между частицами системы; поэтому процессы релаксации весьма многообразны. Время установления равновесия (частичного или полного) в системе называется временем релаксации. 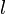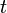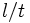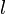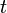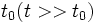Процесс установления равновесия в газах определяется длиной свободного пробега частиц и временем свободного пробега (среднее расстояние и среднее время между двумя последовательными столкновениями молекул). Отношение имеет порядок величины скорости частиц. Величины и очень малы по сравнению с макроскопическими масштабами длины и времени. С другой стороны, для газов время свободного пробега значительно больше времени столкновения . Только при этом условии релаксация определяется лишь парными столкновениями молекул.

Описание процесса релаксации

Для одноатомных газов

В одноатомных газах (без внутренних степеней свободы, то есть обладающих только поступательными степенями свободы) релаксация происходит в два этапа.

На первом этапе за короткий промежуток времени, порядка времени столкновения молекул то, начальное, даже сильно неравновесное, состояние хаотизируется таким образом, что становятся несущественными детали начального состояния и оказывается возможным так называемое «сокращённое описание» неравновесного состояния системы, когда не требуется знания вероятности распределения всех частиц системы по координатам и импульсам, а достаточно знать распределение одной частицы по координатам и импульсам в зависимости от времени, то есть одночастичную функцию распределения молекул. (Все остальные функции распределения более высокого порядка, описывающие распределения по состояниям двух, трёх и т. д. частиц, зависят от времени лишь через одночастичную функцию). Одночастичная функция удовлетворяет кинетическому уравнению Больцмана, которое описывает процесс релаксации. Этот этап называется кинетическим и является очень быстрым процессом релаксации.

На втором этапе за время порядка времени свободного пробега молекул и в результате всего нескольких столкновений в макроскопически малых объёмах системы устанавливается локальное равновесие; ему соответствует локально-равновесное, или квазиравновесное, распределение, которое характеризуется такими же параметрами, как и при полном равновесии системы, но зависящими от пространственных координат и времени. Эти малые объёмы содержат ещё очень много молекул, а поскольку они взаимодействуют с окружением лишь на своей поверхности, их можно считать приближённо изолированными. Параметры локально-равновесного распределения в процессе релаксации медленно стремятся к равновесным, а состояние системы обычно мало отличается от равновесного. Время релаксации для локального равновесия 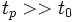. 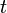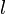После установления локального равновесия для описания релаксации неравновесного состояния системы служат уравнения гидродинамики (уравнения Навье — Стокса, уравнения теплопроводности, диффузии и т. п.). При этом предполагается, что термодинамические параметры системы (плотность, температура и т. д.) и массовая скорость (средняя скорость переноса массы) мало меняются за время и на расстоянии . Этот этап релаксации называется гидродинамическим. Дальнейшая релаксация системы к состоянию полного статистического равновесия, при котором выравниваются средние скорости частиц, средняя температура, средняя концентрация и т. д., происходит медленно в результате очень большого числа столкновений.

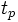
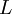
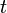
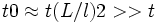
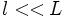
Такие процессы (вязкость, теплопроводность, диффузия, электропроводность и т. п.) называются медленными. Соответствующее время релаксации зависит от размеров системы и велико по сравнению с : , что имеет место при , то есть для не сильно разреженных газов.

Для многоатомных газов

В многоатомных газах (с внутренними степенями свободы) может быть замедлен обмен энергией между поступательными и внутренними степенями свободы, и возникает процесс релаксации, связанный с этим явлением. Быстрее всего — за время порядка времени между столкновениями — устанавливается равновесие по поступательным степеням свободы; такое равновесное состояние можно охарактеризовать соответствующей температурой. Равновесие между поступательными и вращательными степенями свободы устанавливается значительно медленнее. Возбуждение колебательных степеней свободы может происходить лишь при высоких температурах. Поэтому в многоатомных газах возможны многоступенчатые процессы релаксации энергии колебательных и вращательных степеней свободы.

Для смесей газов

В смесях газов с сильно различающимися массами молекул замедлен обмен энергией между компонентами, вследствие чего возможно возникновение состояния с различными температурами компонент и процессы релаксации их температур. Например, в плазме сильно различаются массы ионов и электронов. Быстрее всего устанавливается равновесие электронной компоненты, затем приходит в равновесие ионная компонента, и значительно большее время требуется для установления равновесия между электронами и ионами; поэтому в плазме могут длительное время существовать состояния, в которых ионные и электронные температуры различны а, следовательно, происходят процессы релаксации температур компонент.

Для жидкостей

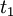
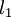
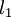
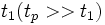
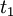
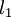
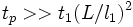
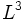
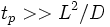
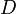
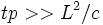
В жидкостях теряет смысл понятие времени и длины свободного пробега частиц (а следовательно, и кинетического уравнения для одночастичной функции распределения). Аналогичную роль для жидкости играют величины и — время и длина корреляции динамических переменных, описывающих потоки энергии или импульса; t₁ и l₁ характеризуют затухание во времени и в пространстве взаимного влияния молекул, то есть корреляции. При этом полностью остаётся в силе понятие гидродинамического этапа релаксации и локально-равновесного состояния. В макроскопически малых объёмах жидкости, но ещё достаточно больших по сравнению с длиной корреляции , локально-равновесное распределение устанавливается за время порядка времени корреляции в результате интенсивного взаимодействия между молекулами (а не парных столкновений, как в газе), но эти объёмы по-прежнему можно считать приближённо изолированными. На гидродинамическом этапе релаксация в жидкости термодинамические параметры и массовая скорость удовлетворяют таким же уравнениям гидродинамики, как и для газов (при условии малости изменения термодинамических параметров и массовой скорости за время и на расстоянии ). Время релаксации к полному термодинамическому равновесию (так же, как в газе и твёрдом теле) можно оценить с помощью кинетических коэффициентов. Например, время релаксации концентрации в бинарной смеси в объёме порядка , где — коэффициент диффузии, время релаксации температуры , где — коэффициент температуропроводности, и т. д. Для жидкости с внутренними степенями свободы молекул возможно сочетание гидродинамического описания поступательных степеней свободы с дополнительными уравнениями для описания релаксации внутренних степеней свободы (релаксационная гидродинамика).

Для твёрдых тел и квантовых жидкостей

В твёрдых телах, как и в квантовых жидкостях, релаксацию можно описывать как релаксацию в газе квазичастиц. В этом случае можно ввести время и длину свободного пробега соответствующих квазичастиц (при условии малости возбуждения системы). Например, в кристаллической решётке при низких температурах упругие колебания можно трактовать как газ фононов. Взаимодействие между фононами приводит к квантовым переходам, то есть к столкновениям между ними. Релаксация энергии в кристаллической решётке описывается кинетическим уравнением для фононов. В системе спиновых магнитных моментов ферромагнетика квазичастицами являются магноны; Релаксацию (например, намагниченности) можно описывать кинетическим уравнением для магнонов. Релаксация магнитного момента в ферромагнетике происходит в два этапа: на первом этапе за счёт относительно сильного обменного взаимодействия устанавливается равновесное значение абсолютной величины магнитного момента.

На втором этапе за счёт слабого спин-орбитального взаимодействия магнитный момент медленно ориентируется вдоль оси лёгкого намагничивания; этот этап аналогичен гидродинамическому этапу релаксации в газах.

См. также

Литература

Лит.: Уленбек Д., форд Дж., Лекции по статистической механике, пер. с англ., М., 1965.

Источник