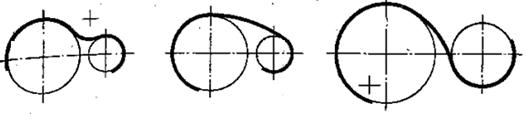Что называется внутренним внешним и смешанным сопряжением

Сопряжения

Практическая работа №8

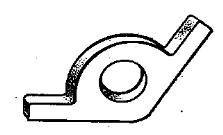
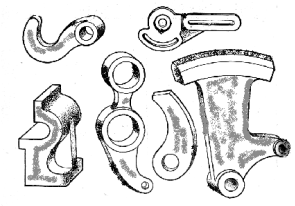
На рис. 1 показаны детали машин. Мы видим, как в их контуре прямая линия плавно переходит в дугу окружности.

Плавный переход одной линии в другую называется сопряжением(рис. 1).

Рисунок 1. Форма детали

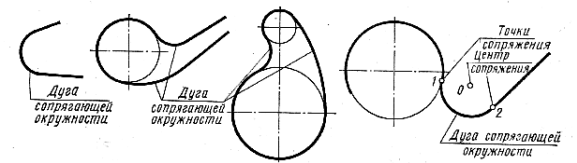
Бывает сопряжение одной прямой с другой прямой, прямой с кривой, одной кривой с другой кривой. Одна линия переходит в другую по дуге окружности. Эта дуга называется дугой сопрягающей окружности(рис. 2). Радиус этой окружности – радиус сопряжения.Центр этой окружности – центр сопряжения.Точка, где одна линия переходит в другую – точка сопряжения.

Сопряжение прямой линии и окружности и сопряжение окружности с окружностью бывает внешнее, внутреннее, смешанное.

Внешнее сопряжение(рис.3,а.). Сопрягаются две окружности. Их центры лежат вне сопрягающей окружности. Такое сопряжение называется внешним.

Внутреннее сопряжение(рис. 3,б). Сопрягаются две окружности. Их центры лежат внутри сопрягающей окружности. Та кое сопряжение называется внутренним.

Смешанное сопряжение(рис. 3,в) Сопрягаются две окружности. Центр одной окружности лежит вне сопрягающей окружности, центр другой окружности лежит внутри сопрягающей окружности. Такое сопряжение называется смешанным.

а) внешнее б) внутреннее в) смешанное

сопряжение сопряжение сопряжение

Рисунок 3. Виды сопряжений

Точки сопряжения зачастую имеют большое значение при проектировании и изготовлении многих изделий, поэтому на учебных чертежах они должны быть определены соответствующими линиями построения,как это сделано на рис.4

Источник

Сопряжение дуг с дугами

Внешнее сопряжение дуг

При внешнем сопряжении центры О₁ и О₂ сопрягаемых дуг радиусов R₁ и R₂ лежат вне сопрягающей дуги радиуса R.

Внешнее сопряжение дуг выполняется в следующей последовательности:

Находим центр сопряжения, точку О пересечения дуг окружностей с радиусами R₁+R и R₂+R соответственно концентричных окружностям с радиусами R₁ и R₂;

Соединяем прямыми центр сопряжения О с центрами окружностей О₁ и О₂, которые пересекаясь с заданными окружностями определяют положение точек сопряжения А и В;

Внутреннее сопряжение дуг

При внутреннем сопряжении центры О₁ и О₂ сопрягаемых дуг радиусов R₁ и R₂ лежат внутри сопрягающей дуги радиуса R.

Внутреннее сопряжение дуг выполняется в следующей последовательности:

Находим центр сопряжения, точку О пересечения дуг окружностей с радиусами R-R₁ и R-R₂ соответственно концентричных окружностям с радиусами R₁ и R₂;

Соединяем прямыми центр сопряжения О с центрами окружностей О₁ и О₂, которые пересекаясь с заданными окружностями определяют положение точек сопряжения А и В;

Смешанное сопряжение дуг

При смешанном сопряжении центр О₂ одной из сопрягаемых дуг лежит внутри сопрягающей дуги радиуса R, а центр О₁ другой сопрягаемой дуги вне ее.

Внутреннее сопряжение дуг выполняется в следующей последовательности:

Находим центр сопряжения, точку О пересечения дуг окружностей с радиусами R+R₁ и R-R₂ соответственно концентричных окружностям с радиусами R₁ и R₂;

Соединяем прямыми центр сопряжения О с центрами окружностей О₁ и О₂, которые пересекаясь с заданными окружностями определяют положение точек сопряжения А и В;

Источник

Что называется внутренним внешним и смешанным сопряжением

При вычерчивании деталей машин и приборов, кон­туры очертаний которых состоят из прямых линий и дуг окружностей с плавными переходами от одной линии в другую, часто применяют сопряжения. Сопря­жением называется плавный переход одной линии в другую. На рис. 60 показаны примеры применения сопряжений.

Контур рычага (рис. 60а) состоит из отдельных линий, плавно переходящих одна в другую, например, в точках А, А₁ виден плавный переход от дуги окруж­ности к прямой линии, а в точках В, В₁ — от дуги одной окружности к дуге другой окружности (рис. 60, б). На рис. 60, в изображен двурогий крюк. На чертеже кон­тура крюка (рис. 60, г) в точке А виден плавный пере­ход от дуги окружности D=200 к прямой линии, а в точке В — от дуги окружности радиуса R460 к дуге ра­диуса R260.

Для точного и правильного выполнения чертежей необходимо уметь выполнять построения сопряжений, которые основаны на двух положениях.

СОПРЯЖЕНИЕ ДВУХ СТОРОН УГЛА ДУГОЙ ОКРУЖНОСТИ ЗАДАННОГО РАДИУСА

При выполнении чертежей деталей, показанных на рис. 62, б, г, е, выполняют построение сопряжения двух сторон угла дугой окружности заданного радиуса. На рис. 62, а выполнено построение сопряжения сто­рон острого угла дугой, на рис. 62, в — тупого угла, на рис. 62, д — прямого.

Сопряжение двух сторон угла (острого или тупого) дугой заданного радиуса R выполняют следующим образом (рис. 62, а и в).

Параллельно сторонам угла на расстоянии, равном радиусу дуги R, проводят две вспомогательные прямые линии. Точка пересечения этих прямых (точка О) будет центром дуги радиуса Я, т. е. центром сопряже­ния. Из центра О описывают дугу, плавно переходя­щую в прямые — стороны угла. Дугу заканчивают в точках сопряжения n и n₁ которые являются Основаниями перпендикуляров, опущенных из центра О на сто­роны угла.

СОПРЯЖЕНИЕ ПРЯМОЙ С ДУГОЙ ОКРУЖНОСТИ

Сопряжение прямой с дугой окружности может быть выполнено при помощи дуги с внутренним касанием (рис. 63, в) и дуги с внешним касанием (рис. 63, а).

На рис. 63, а показано сопряжение дуги окружности радиусом R и прямой линии А В дугой окружности радиуса r с внешним касанием. Для построения такого сопряжения проводят окружность радиуса R и прямую АВ. Параллельно заданной прямой на расстоянии, рав­ном радиусу r (радиус сопрягающей дуги), проводят прямую ab. Из центра О проводят дугу окружности

радиусом, равным сумме радиусов и r, до пересече­ния ее с прямой ab в точке О₁ Точка О₁ является цент­ром дуги сопряжения.

Точку сопряжения с находят на пересечении прямой 00 ₁ с дугой окружности радиуса R. Точка сопряжения C₁ является основанием перпендикуляра, опущенного из центра О₁ на данную прямую При помощи ана­логичных построений могут быть найдены точки 0₂,

На рис. 63, б показан кронштейн, при вычерчивании контура которого необходимо выполнить построения, описанные выше.

На рис. 63, в выполнено сопряжение дуги радиуса R с прямой А В дугой радиуса r с внутренним касанием. Центр дуги сопряжения О₁ находится на пересечении вспомогательной прямой, проведенной параллельно данной прямой на расстоянии r, с дугой вспомогатель­ной окружности, описанной из центра О радиусом, рав­ным разности R—r. Точка сопряжения является основанием перпендикуляра, опущенного из точки О₁ на данную прямую. Точку сопряжения с находят на пересечении прямой ОО₁ с сопрягаемой дугой. Такое сопряжение выполняют, например, при вычерчивании контура маховика, показанного на рис. 63, г.

СОПРЯЖЕНИЕ ДУГИ С ДУГОЙ

Сопряжение двух дуг окружностей может быть вну­тренним, внешним и смешанным.

При внутреннем сопряжении центры O и O₁ сопря­гаемых дуг находятся внутри сопрягающей дуги ради­уса R (рис. 64, б).

При внешнем сопряжении центры и сопрягае­мых дуг радиусов R₁ и R₂ находятся вне сопрягающей дуги радиуса R (рис. 64, в).

При смешанном сопряжении центр О, одной из сопрягаемых дуг лежит внутри сопрягающей дуги

радиуса R, а центр О другой сопрягаемой дуги вне ее (рис. 65, а).

На рис. 64, а показана деталь (серьга), при вычерчи­вании которой необходимо построение внутреннего и внешнего сопряжения.

Построение внутреннего сопряжения.

а) радиусы сопрягаемых окружностей R₁ и R₂

б) расстояния l₁ и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

а) определить положение центра 0₂ сопрягающей дуги;

б) найти точки сопряжения s₁ и s

в) провести дугу сопряжения.

Построение сопряжения показано на рис. 64, б. По заданным расстояниям между центрами 1₁ и l₂ на чер­теже намечают центры О и O₁ из которых описывают сопрягаемые дуги радиусов R₁ и R₂. Из центра О₁ про­водят вспомогательную дугу окружности радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой R₂, а из центра О — радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой R₁ Вспомогательные дуги пересекутся в точке 0₂ которая и будет искомым центром сопрягающей дуги.

Для нахождения точек сопряжения точку 0₂ соеди­няют с точками О и О₁ прямыми линиями. Точки пере­сечения продолжения прямых 0₂0 и 0₂0 с сопрягае­мыми дугами являются искомыми точками сопряжения (точки S и s₁).

Радиусом R из центра О_г проводят сопрягающую дугу между точками сопряжения s и s₁

Построение внешнего сопряжения.

б) расстояния и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

а) определить положение центра 0₂ сопрягающей дуги;

б) найти точки сопряжения и s₁;

в) провести дугу сопряжения.

Построение внешнего сопряжения показано на рис. 64, в. По заданным расстояниям между центрами l₁ и l₂ на чертеже находят точки О и О₁ из которых описывают сопрягаемые дуги радиусов R₁ и R₂. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягаемой дуги R₁, и сопряга­ющей R, а из центра О₁ — радиусом, равным сумме

радиусов сопрягаемой дуги R₂ и сопрягающей R. Вспо­могательные дуги пересекутся в точке O₂, которая будет искомым центром сопрягающей дуги Для нахождения точек сопряжения центры дуг сое-

диняют прямыми линиями 00₂ и 010₂. Эти две пря­мые пересекают сопрягаемые дуги в точках сопряже­ния S и s1

Из центра 0₂ радиусом R проводят сопрягающую ду­гу, ограничивая ее точками сопряжения и

Построение смешанного сопряжения. Пример сме­шанного сопряжения приведен на рис. 65, и где изображены кронштейн и его чертеж.

б) расстояния l₁ и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

а) определить положение центра 0₂ сопрягающей дуги;

б) найти точки сопряжения s и s₁

в) провести дугу сопряжения.

По заданным расстояниям между центрами l₁ и l₂ на чертеже намечают центры 0 и 0₁, из которых описы­вают сопрягаемые дуги радиусов R₁ и R₂. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягаемой дуги R₁ и сопрягающей R, а из центра 0₁ — радиусом, равным разности радиусов R и R₂. Вспомогательные дуги пересекутся в точке 0₂, которая будет искомым центром сопряга­ющей дуги.

Соединив точки О и 0₂ прямой, получают точку сопряжения соединив точки О₁ и 0₂, находят точку сопряжения s. Из центра 0₂ проводят дугу сопряжения от s до s₁

При вычерчивании контура детали необходимо разо­браться, где имеются плавные переходы, и предста­вить себе, где надо выполнить те или иные виды сопря­жения.

Для приобретения навыков построения сопряжения выполняют упражнения по вычерчиванию контуров сложных деталей. Перед упражнением необходимо просмотреть задание, наметить порядок построения сопряжений и только после этого приступить к выпол­нению построений.

На рис. 66, а изображена деталь (кронштейн), а на рис. 66, б, в, г показана последовательность выполне­ния контурного очертания этой детали с построением различных видов сопряжений.

Источник

Сопряжения

Очертания многих предметов представляют собой сочетание ряда линий, в большинстве своём плавно переходящих одна в другую.

Плавный переход одной линии в другую называют касанием, а точку, в которой происходит касание, точкой касания или перехода (рис. 49).

Через любую точку касания можно провести общую касательную, которая будет перпендикулярна к радиусам дуг, проведенным в точку касания.

Плавный переход одной линии в другую при помощи промежуточной линии называют сопряжением. На рис. 50 такой линией является дуга АВ радиуса Rc. Её называют дугой сопряжения, радиус R c — радиусом сопряжения, а центр сопрягающей дуги – центром сопряжения.

При сопряжении всегда имеются две точки перехода и через каждую из них можно провести по одной общей касательной.

Таким образом, построение сопряжений основано на свойствах касательной к дуге окружности и касания двух дуг окружностей.

Построение касательной к окружности в заданной на ней точке.

Через точку А и центр О (рис. 51) проводят прямую и в точке А восстанавливают к ней перпендикуляр (построение перпендикуляра к прямой в заданной на ней точке рассмотрено на рис. 32).

Построение касательной к окружности из точки А вне окружности.

Из точки О₁ описывают окружность радиусом O₁ A, которая пересекает заданную окружность в точках касания В и С.

Построение касательных окружностей.

При внутреннем касании расстояние между центрами касающихся окружностей равно разности радиусов R-r. Точка касания А расположена на продолжении прямой, соединяющей центры О₁ и О₂ (рис. 53б).

Построение общей внешней касательной к двум окружностям.

Из центра O 1 большей окружности описывают окружность радиусом R-r (рис. 54а).

Обе проведенные окружности пересекаются в точках А и В. Точки O₁ и В соединяют прямой и в пересечении её с окружностью радиуса R определяют точку касания D (рис. 54б). Из точки О 2 параллельно прямой O₁ D проводят линию до пересечения с окружностью радиуса г и получают вторую точку касания С.

Построение общей внутренней касательной к двум окружностям.

Сопряжение двух пересекающихся прямых дугой заданного радиуса.

Проводят две прямые, параллельные заданным и удалённые от них на величину радиуса Rc (рис. 56а). В пересечении отмечают точку О – центр сопряжения. Из точки О опускают перпендикуляры на заданные прямые и получают точки касания А и В дуги сопряжения. Такое построение справедливо для любого угла между заданными прямыми.

Для сопряжения сторон прямого угла можно воспользоваться способом, указанным на рис. 56б.

Сопряжение дуги и прямой дугой окружности заданного радиуса.

Может быть два случая такого сопряжения: внешнее касание сопрягающей дуги с заданной (рис. 57а) и внутреннее (рис. 57б). При внешнем касании из центра О₁ проводят дугу радиусом R+R c и прямую, параллельную заданной, на расстоянии R c от неё. На пересечении получают точку О центра сопряжения. На прямой ОО₁ отмечают точку касания А. Точку В касания получают, опустив перпендикуляр из центра О на заданную прямую.

При внутреннем касании построения аналогичны, только радиус вспомогательной дуги равен Rс-R.

Сопряжение двух дуг дугой окружности заданного радиуса.

Различают три вида такого сопряжения: внешнее, внутреннее и смешанное.

При смешанном сопряжении (рис. 58в) построения аналогичны и ясны из чертежа.

Источник

Сопряжение линий с примерами и образцами выполнения

Содержание:

При вычерчивании деталей, контуры очертаний которых состоят из прямых линий и дуг окруж­ностей с плавными переходами от одной линии в другую, часто выполняют сопряжения. Сопряже­нием называется плавный переход одной линии в другую. На рис. 60 показаны примеры примене­ния сопряжений.

Контур рычага (рис. 60, а) состоит из отдель­ных линий, плавно переходящих одна в другую, например, в точках А, виден плавный переход от дуги окружности к прямой линии, а в точках В, В₁ — от дуги одной окружности к дуге другой окружности (рис. 60, б). На рис. 60, в изображен двурогий крюк. На чертеже контура крюка (рис. 60, г) в точке А виден плавный переход от дуги окружности (200) к прямой линии, а в точке В — от дуги окружности (R 460) к дуге окружности (R260).

Для точного и правильного выполнения черте­жей необходимо уметь выполнять построения сопряжений, которые основаны на двух поло­жениях.

1. Для сопряжения прямой линии и дуги необходимо, чтобы центр окружности, которой принадлежит дуга, лежал на перпендикуляре к пря­мой, восставленном из точки сопряжения (рис. 62, а).

2. Для сопряжения двух дуг необходимо, чтобы центры окружностей, которым принадлежат дуги, лежали на прямой, проходящей через точку со­пряжения (рис. 61, б).

Сопряжение двух сторон угла дугой окружности и заданного радиуса

При выполнении чертежей деталей, показан­ных на рис. 62, б, г, е, выполняют построение сопряжения двух сторон угла дугой окружности заданного радиуса. На рис. 62, а выполнено по­строение сопряжения сторон острого угла дугой, на рис. 62, в — тупого угла, на рис. 62, д — пря­мого.

Сопряжение двух сторон угла (острого или тупого) дугой заданного радиуса Rвыполняют следующим образом (рис. 62, а и в).

Параллельно сторонам угла на расстоянии, равном радиусу дуги R,проводят две вспомога­тельные прямые линии. Точка пересечения этих прямых (точка О) будет центром дуги радиуса R, т.е. центром сопряжения. Из центра О описывают дугу, плавно переходящую в прямые — стороны угла. Дугу заканчивают в точках сопряжения п и п₁ которые являются основаниями перпендику­ляров, опущенных из центра О на стороны утла.

При построении сопряжения сторон прямого угла центр дуги сопряжения проще находить с помощью циркуля (рис. 62, д). Из вершины угла А проводят дугу радиусом R,равным радиусу сопряжения. На сторонах утла получают точки сопряжения п и п₁. Из этих точек, как из цен­тров, проводят дуги радиусом Rдо взаимного пересечения в точке О, являющейся центром со­пряжения. Из центра О описывают дугу сопряже­ния.

Сопряжение прямой с дугой окружности

Сопряжение прямой с дугой окружности может быть выполнено с помощью дуги с внутренним касанием (рис. 63, в) и дуги с внешним касанием (рис. 63, а).

На рис. 63, а показано сопряжение дуги окруж­ности радиусом Rи прямой АВ дугой окружности радиуса r с внешним касанием. Для построения такого сопряжения проводят окружность радиуса R и прямую AB. Параллельно заданной прямой на расстоянии, равном радиусу r (радиус сопрягаю­щей дуги), проводят прямую ab. Из центра О проводят дугу окружности радиусом, равным сум­ме радиусов R и г, до пересечения ее с прямой ab в точке O₁. Точка О₁ является центром дуги со­пряжения.

Точку сопряжения с находят на пересечении прямой ОO₁ с дугой окружности радиуса R. Точка сопряжения c₁ является основанием перпендику­ляра, опущенного из центра O₁ на данную пря­мую АB. С помощью аналогичных построений могут быть найдены точки О₂c₂c₃

На рис. 63, б показан кронштейн. При вы­полнении изображения контура этой детали необходимо выполнить построения, описанные выше.

На рис. 63, в выполнено сопряжение дуги ради­уса Rc прямой AВ дугой радиуса r с внутренним касанием. Центр дуги сопряжения О₁ находится на пересечении вспомогательной прямой, прове­денной параллельно данной прямой на расстоянии г, с дугой вспомогательной окружности, описан­ной из центра О радиусом, равным разности R—r. Точка сопряжения является основанием перпенди­куляра, опущенного из точки О₁ на данную пря­мую. Точку сопряжения с находят на пересечении прямей ОО₁ с сопрягаемой дугой. Такое сопряже­ние выполняют, например, при вычерчивании контура маховика, показанного на рис. 63, г.

Сопряжение дуги с дугой

Сопряжение двух дуг окружностей может быть внутренним, внешним и смешанным.

При внутреннем сопряжении центры О и О₁ сопрягаемых дуг находятся внутри сопрягающей дуги радиуса R (рис. 64, б).

При внешнем сопряжении центры О И О₁ сопрягаемых дуг радиусов R₁ и R₂ находятся вне сопрягающей дуги радиуса R (рис. 64. в).

При смешанном сопряжении центр О₁ одной из сопрягаемых дут лежит внутри сопрягающей дуги радиуса R, а центр О другой сопрягаемой дуги вне ее (рис. 65. а).

На рис. 64, а показана деталь (серьга), при вычерчивании которой необходимо по­строение внутреннего и внешнего сопряжения (рис. 64, б—г).

Построение внутреннего сопряжения.

а) радиусы сопрягаемых окружностей R₁ и R₂;

б) расстояния l₁ и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

г) определить положение центра О₂ сопрягаю­щей дуги;

д) найти точки сопряжения s и s₁;

е) провести дугу сопряжения.

Построение сопряжения показано на рис. 64, б. По заданным расстояниям между центрами l₁ и l₂ на чертеже намечают центры О и О₁, из которых описывают сопрягаемые дуги радиусов R₁ и R₂. Из центра О₁ проводят вспомогательную дугу окружности радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой R₂, а из цен­тра О — радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой R₁. Вспомога­тельные дуги пересекутся в точке О₂, которая и будет искомым центром сопрягающей дуги.

Для нахождения точек сопряжения точку О₂ соединяют с точками О и О₁ прямыми линиями. Точки пересечения продолжения прямых О₂О и О₂О₁ с сопрягаемыми дугами являются искомыми точками сопряжения (точки s и s₁).

Радиусом R из центра О₂ проводят сопрягаю­щую дугу между точками сопряжения s и s_1.

Построение внешнего сопряжения

а) радиусы R₁ и R₂ сопрягаемых дуг окружнос­тей;

б) расстояния l₁ и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

а) определить положение центра О₂ сопрягаю­щей дуги;

б) найти точки сопряжения s и s₁;

в) провести дугу сопряжения.

Построение внешнего сопряжения показано на рис. 64, в. По заданным расстояниям между цен­трами l₁ и l₂ на чертеже находят точки О и О₁, из которых описывают сопрягаемые дуги радиусов R₁ и R₂. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиу­сов сопрягаемой дуге R₁ и сопрягающей R, а из центра О₁ — радиусом, равным сумме радиусов сопрягаемой дуги R₂ и сопрягающей R. Вспомога­тельные дуги пересекутся в точке О₂, которая будет искомым центром сопрягающей дуга.

Для нахождения точек сопряжения центры дуг соединяют прямыми линиями ОО₂ и О₁О₂. Эти две прямые пересекают сопрягаемые дуга в точ­ках сопряжения s и s₁.

Из центра О₂ радиусом R проводят сопрягаю­щую дугу, ограничивая ее точками сопряжения s и s_1.

Построение смешанного сопряжения

Пример смешанного сопряжения приведен на рис. 65, а—в.

а) радиусы R₁ и R₂ сопрягаемых дут окружнос­тей;

б) расстояния и l₁ и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

а) определить положение центра О₂ сопрягаю­щей дуги;

б) найти точки сопряжения s и s₁;

в) провести дугу сопряжения.

По заданным расстояниям между центрами l₁ и l₂ на чертеже намечают центры О и О₁, из ко­торых описывают сопрягаемые дуги радиусов R₁ и R₂. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиу­сов сопрягаемой дуги R₁ и сопрягающей R, а из центра О₁ — радиусом, равным разности радиусов R и R₂. Вспомогательные дуги пересекутся в точ­ке О₂, которая будет искомым центром сопрягаю­щей дуги.

Соединив точки О и О₂ прямой, получают точ­ку сопряжения s₁, соединив точки О₁ и О₂ нахо­дят точку сопряжения s. Из центра О₂ проводят дугу сопряжения от s до s₁.

При вычерчивании контуров сложных деталей важно уметь распознавать в плавных переходах те или иные виды сопряжений и уметь их вычерчи­вать.

Для приобретения навыков в построении сопря­жений выполняют упражнения по вычерчиванию контуров сложных деталей. Для этого необходимо определить порядок построения сопряжений и только после этого приступать к их выполнению.

На рис. 66 изображена деталь (кронштейн) и последовательность выполнения контурного очер­тания этой детали с построением различных видов сопряжений.

Примеры и образцы решения задач:

Услуги по выполнению чертежей:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник