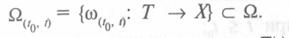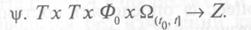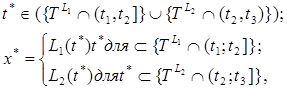Что называется входной выходной ситуацией для системы в данный момент времени

Раздел 1. Общие сведения об ИС

Тема 1.1. Общая характеристика ИС

Лекция 1. Основные понятия ИС

План:

1. Системный анализ. Его основные понятия и определения.

2. Структурное строение систем.

3. Терминальное представление систем.

4. Моделирование систем.

5. Классификация систем.

Системным анализом называется раздел науки, посвященный ис­следованию, описанию и реализации систем различной природы и характера.

Каждая система может быть отнесена к определенной части реаль­ного мира, называемой предметной областью.

Системой называется целостная совокупность взаимосвязанных элементов, обладающая свойствами, которые не сводятся к свойст­вам этих элементов и не выводятся из них.

Свойства системы:

• членимость на составляющие элементы;

Подсистемой некоторой системы называется совокупность ее эле­ментов, которая сама является системой.

Среда является внешним окружением системы. Взаимодействие си­стемы и среды характеризуется:

Система называется замкнутой, если взаимодействие со средой от­сутствует или им можно пренебречь; в противном случае система называется открытой.

Система называется связной, если возможен обмен ресурсами меж­ду любыми двумя ее подсистемами.

Структурное строение систем

Структуры систем бывают разного типа, разной топологии:

— иерархические (древовидные) структуры

Система называется сложной, если образующие ее элементы сами являются системами.

Процесс последовательного членения системы на образующие ее подсистемы называется декомпозицией.

Для любой системы более низкого уровня система более высокого уровня называется надсистемой или суперсистемой.

Система называется большой, если в ее описании существенное зна­чение имеют пространственные (географические) факторы.

Множество элементов системы, посредством которых среда влияет на систему, называется входным полюсом системы.

Множество элементов системы, посредством которых система влияет на среду, называется выходным полюсом системы.

Мгновенная характеристика влияния среды на систему на входном полюсе системы называется входной ситуацией для системы в дан­ный момент времени.

Мгновенная характеристика влияния среды на систему на выход­ном полюсе системы называется выходной ситуацией для системы в данный момент времени.

Процесс изменения входной ситуации во времени называется входным процессом системы или входным воздействием на систему.

Процесс изменения выходной ситуации во времени называется вы­ходным процессом системы или реакцией системы.

Принцип причинности

Принцип причинности, широко используемый для исследования систем, выражается в виде двух тезисов.

• Упорядоченность причинно-следственных связей во времени. Выходная ситуация системы в любой момент времени не зави­сит от ситуаций, которые могут возникнуть на входном полюсе системы в более поздние моменты времени.

• Однозначность причинно-следственных связей во времени. Вы­ходная ситуация системы в любой момент времени в будущем может быть определена однозначно, если известны:

— все сведения о системе, характеризующие ее и воздействие на нее среды в прошлом и настоящем;

— входное воздействие на систему в будущем.

Система, удовлетворяющая принципу причинности, называется ди­намической системой. Все реальные системы являются динамическими.

Состоянием системы называется совокупность характеристик сис­темы, однозначно определяющих, при известном входном воздейст­вии, выходную ситуацию в будущем.

Процесс изменения состояния динамической системы во времени называется движением динамической системы.

Динамическая система с фиксированным состоянием называется кинематической системой.

Кинематическая система, у которой входная и выходная ситуации неизменны во времени (являются константами), называется стати­ческой системой.

Кинематические и статические системы, получаемые из динамичес­ких, часто используются для упрощения исследований при решении многих прикладных задач.

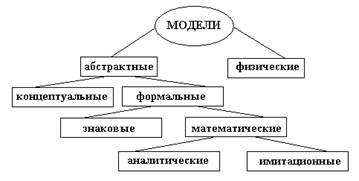
Моделью системы называется вспомогательная система, находяща­яся в объективном соответствии с изучаемой системой и позволяю­щая получать информацию об этой системе (рисунок 1).

Рисунок 1 – Классификация моделей

Классификация систем

1. По отношению к среде выделяют системы:

2. По происхождению выделяют системы:

3. По описанию переменных системы могут быть:

• с качественными переменными;

• с количественными переменными;

• ‘ со смешанными переменными.

4. По типу описания закона (законов) функционирования:

5. По способу управления в системе:

• управляемые извне системы;

• управляемые изнутри системы;

• с комбинированным управлением.

Вопросы для самоконтроля:

1. Что изучает системный анализ?

2. Что такое система, подсистема, среда?

3. Какие основные структурные топологии систем Вы знаете?

4. Какая система называется замкнутой?

5. Какая система называется открытой?

6. Какая система называется связной?

7. Какая система называется сложной?

8. Какая система называется большой?

9. Какой процесс называется декомпозицией?

10. Какой процесс называется агрегированием?

11. Что называется входным (выходным) полюсом системы?

12. Что называется входной (выходной) ситуацией для системы в данный момент времени?

13. Что называется входным (выходным) процессом системы?

14. Что называется моделью системы? Какие классы моделей Вы знаете?

15. По каким признакам классифицируют информационные системы?

Источник

2 предмет конспекты. Борисова Марина Валентиновна, преподаватель Иркутск 2015 г. Содержание пояснительная записка 5 Раздел Общие сведения об ис 8 Тема Общая характеристика ис 8 лекция

Раздел 1. Общие сведения об ИС

Тема 1.1. Общая характеристика ИС

Лекция 1. Основные понятия ИС

Системным анализом называется раздел науки, посвященный ис­следованию, описанию и реализации систем различной природы и характера.

Каждая система может быть отнесена к определенной части реаль­ного мира, называемой предметной областью.

Системой называется целостная совокупность взаимосвязанных элементов, обладающая свойствами, которые не сводятся к свойст­вам этих элементов и не выводятся из них.

Система называется связной, если возможен обмен ресурсами меж­ду любыми двумя ее подсистемами.

Структурное строение систем

Процесс последовательного членения системы на образующие ее подсистемы называется декомпозицией.

Для любой системы более низкого уровня система более высокого уровня называется надсистемой или суперсистемой.

Система называется большой, если в ее описании существенное зна­чение имеют пространственные (географические) факторы.

Множество элементов системы, посредством которых среда влияет на систему, называется входным полюсом системы.

Множество элементов системы, посредством которых система влияет на среду, называется выходным полюсом системы.

Мгновенная характеристика влияния среды на систему на входном полюсе системы называется входной ситуацией для системы в дан­ный момент времени.

Мгновенная характеристика влияния среды на систему на выход­ном полюсе системы называется выходной ситуацией для системы в данный момент времени.

Процесс изменения входной ситуации во времени называется входным процессом системы или входным воздействием на систему.

Процесс изменения выходной ситуации во времени называется вы­ходным процессом системы или реакцией системы.

Состоянием системы называется совокупность характеристик сис­темы, однозначно определяющих, при известном входном воздейст­вии, выходную ситуацию в будущем.

Процесс изменения состояния динамической системы во времени называется движением динамической системы.

Динамическая система с фиксированным состоянием называется кинематической системой.

Кинематическая система, у которой входная и выходная ситуации неизменны во времени (являются константами), называется стати­ческой системой.

Кинематические и статические системы, получаемые из динамичес­ких, часто используются для упрощения исследований при решении многих прикладных задач.

Моделью системы называется вспомогательная система, находяща­яся в объективном соответствии с изучаемой системой и позволяю­щая получать информацию об этой системе (рисунок 1).

Рисунок 1 – Классификация моделей
Классификация систем

Источник

Характеристика процессов системы

Процессы системы — это совокупность последовательных изменений состояния системы для достижения цели.

К процессам системы относятся:

переходный процесс системы.

Входной процесс — множество входных воздействий, которые изменяются с течением времени.

Входной процесс можно задать, если каждому моменту времени t поставить в соответствие по определенному правилу со входные воздействия х с X. Моменты времени t определены на множестве Т, t Î Т. В результате этот входной процесс будет представлять собой функцию времени 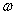: Т® Y [х].

Функции входных процессов — задание по определенному правилу, в определенные моменты времени управляющих воздействий.

Выходной процесс множество выходных воздействий на окружающую среду, которые изменяются с течением времени.

Воздействие системы на окружающую среду определяется выходными величинами (реакциями). Выходные величины изменяются с течением времени, образуя выходной процесс, представляющий функцию у: Т ® Y[X].

Функции выходных процессов — задание по определенному правилу, в определенные моменты времени выходных величин (реакций) системы.

Множество допустимых функций, характеризующих выходной процесс, обозначим Г = . Для обозначения мгновенных значений выходных величин в моменты t можно использовать обозначения y(t) [х].

Множество допустимых входных процессов, определяемых различными функциями на интервале [t0, t], описывается следующим образом:

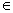
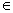
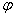
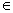
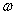
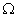
Следовательно, состояние Z(t) системы в момент времени t будет зависеть от начального момента t0 Т, текущего времени t Т, начального движения 0 Ф0 на отрезке [t — v, t0] и входного процесса (t0, t] (t0,t) на интервале (t0,t)

Таким образом, состояние Z(t) может быть определено с помощью переходной функции состояния:

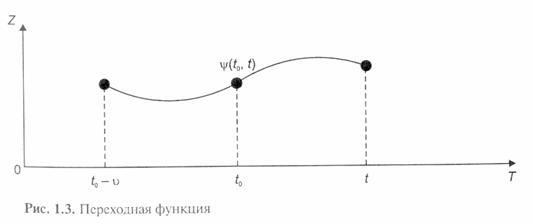
Графически переходная функция представлена на рис. 1.3.

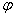
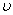
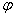
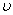
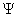
На рис. 1.3 отрезок движения системы на промежутке [t0 — , t] будет представлять собой сочленение двух отрезков: 0 — начального движения на промежутке [t0 , t0] и (t0,t) — отрезка переходной функции на интервале (t0, t].

Переходная функция состояния должна удовлетворять следующим требованиям.

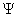
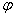
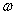
Z(t) = (t, t0, 0, (t0,t])

должно быть определено во всех t ³ t0 — .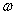

Во-вторых, переходная функция состояния должна быть согласована с начальным движением и начальным состоянием

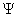
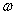
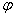
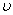
Z(t) = (t, t0, (to,t]) = 0(t, t0, ) при t £ t0 ;

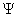
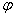
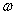
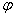
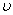
Z(to) = (t, t0, 0, (to,t]) = 0(t, t0, ) при t £ t0 ;

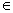
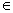
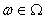
для всех t T, z Z, ,. Эти условия устанавливают также независимость начального движения 0 и начального состояния Z(t0) от значений входного процесса, поскольку (to,t]= 0 при t £ t0.

В-третьих, один и тот же входной процесс со определяет состояние системы на конце интервала времени (t0, t] независимо от того, действовал ли он последовательно, сначала на интервале (t0, t], а затем на интервале (t’, t], или на всем интервале (t0, t].

Переходная функция состояния описывает переходный процесс системы.

Переходный процесс системы (процесс системы) — множество преобразований начального состояния и входных воздействий в выходные величины, которые изменяются с течением времени по определенным правилам.

Функцией входа является возбуждение той силы, которая обеспечивает систему энергией, материалом, информацией, поступающей в процесс.

В зависимости от связей входные процессы могут принимать одну (или более) из следующих форм:

1) результат предшествующего процесса, последовательно связанный с данным процессом;

2) результат предшествующего процесса, беспорядочно связанный с данным процессом;

3) результат процесса данной системы, который вновь вводится в нее.

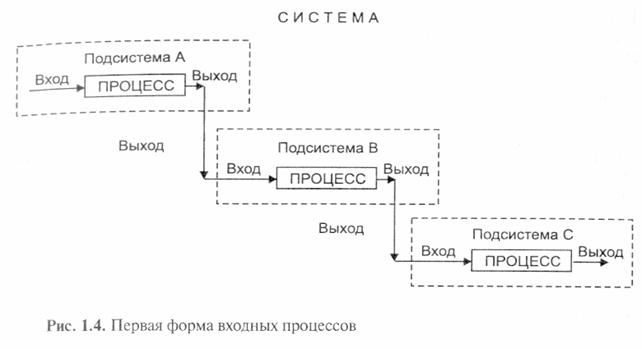
Пример первой формы входных процессов показан на рис. 1.4.

На рис. 1.4 в процессах В и С выходной процесс предыдущей подсистемы вводится без изменений как входной процесс в следующий процесс системы. Процесс А в этом примере является более ранней по времени подсистемой, но не обязательно более простой или более сложной.

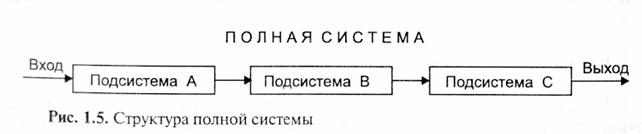
Подсистемы А, В и С объединяются в полную систему.

Если несколько подсистем объединены для формирования конечного выхода, частные процессы А, В, С и т.д. связаны так, как показано на рис. 1.5.

Полная система состоит из всех подсистем, свойств и связей, необходимых для достижения данной цели при данных принуждающих связях. Цель полной системы определяет результат, для достижения которого организуются все ее подсистемы, свойства и связи. Принуждающие связи системы являются ограничениями, накладываемыми на ее действия. Они определяют границу полной системы и дают возможность точно установить условие, при котором она должна действовать.

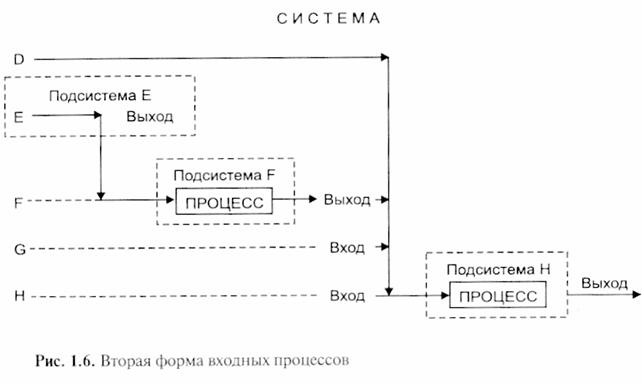
Вторая форма входных процессов называется беспорядочной (рис. 1.6).

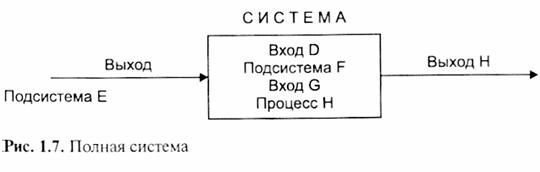
В этом случае входные процессы подсистемы D и G являются входами, вводимыми в случайные моменты времени. Подсистемы D, F, G и Н можно представить как части единого процесса — полную систему (рис. 1.7).

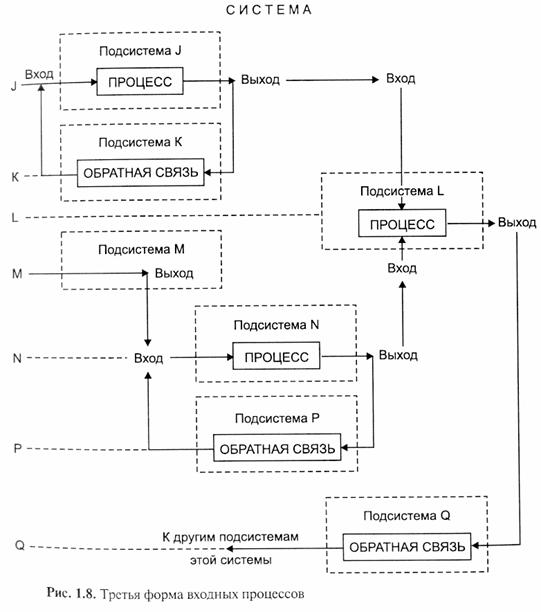
Третья форма входных процессов отличается тем, что в этом случае вход вводится в систему будучи до этого выходом этой же системы. Этот случай иллюстрируется рис. 1.8, где подсистемы К, Р и Q имеют входные процессы связанные с процессом обратной связи.

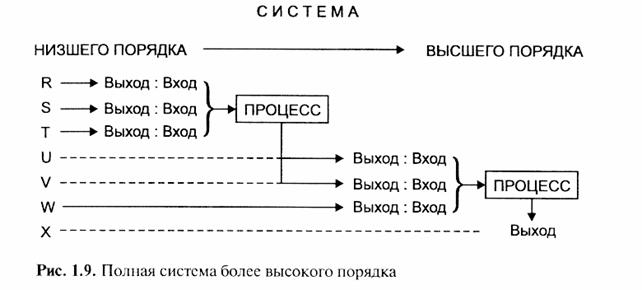
Рассмотрим процесс «Выход : Вход» между подсистемами более высокого порядка (рис. 1.9).

Чтобы обеспечить подходящий вход в подсистему более высокого порядка, выходы, как это показано на рис. 1.9, могут быть взаимно причинно зависимы. Подсистемы R, S и Т по времени предшествуют подсистемам U, V и X. Они с необходимостью должны предшествовать им, чтобы система могла работать; подсистемы U и V имеют более высокий приоритет по сравнению с R, S, Т и W, но более низкий приоритет, чем подсистема X.

Выход, обозначенный на рис. 1.9 как «Выход : Вход», может автоматически становиться входом, если он вводится в последующую подсистему без изменений, т.е. в этом случае выход и вход идентичны.

Процессы R, S, Т и U, V, W имеют один выход X. Выход W является выходам от внешней подсистемы, и поэтому он не связан с предыдущей последовательностью системных процессов, имеющих выходы U и V. Никаких ограничений на число выходов во внешнюю среду, кроме возможностей человека и машины воспринимать их, не существует.

Единственное назначение подсистем обратной связи — изменение идущего процесса.

Обратная связь может быть:

1) объектом отдельного процесса подсистемы;

2) объектом интегрированного процесса подсистемы;

3) распределенным по времени объектом, возвращающим выход подсистемы с высшим приоритетом (более поздний по времени) для сравнения с критерием подсистемы низшего приоритета (более раннего по времени).

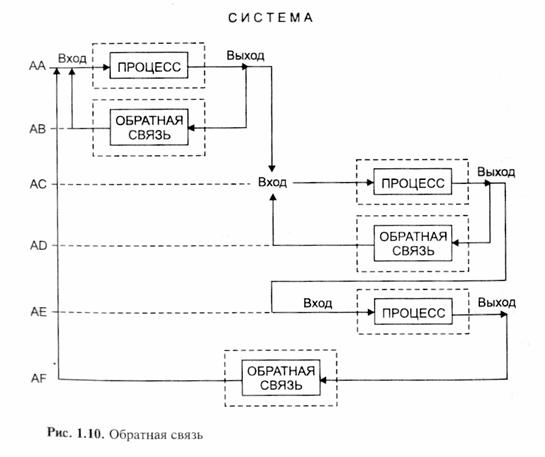
Схема на рис. 1.10 позволяет пояснить перечисленные виды процессов подсистемы обратной связи.

Интегрированным процессом называется такой, в котором объекты подсистемы теряют свой независимый характер. В интегрированных системах объекты могут быть определены только в контексте подсистемы или системы, к которой они принадлежат.

Подсистема АА на рис. 1.10 предшествует двум подсистемам АВ и АС. Но она играет по отношению к ним разные роли: обратная связь АВ дает вход в подсистему АА (выступает как обратная связь объекта отдельного процесса подсистемы), но, кроме того, выход используется как вход в подсистему АС.

Выход подсистемы АС поступает на входную сторону подсистемы АЕ. Подсистемы АА, АС и АЕ видоизменяются собственными функциями подсистем обратной связи (обратная связь выступает как объект интегрированного процесса подсистем). Кроме того, подсистемы АА, АС, АЕ также изменяются под воздействием результатов последующих действий, например, подсистема АЕ изменяет подсистему АА с помощью обратной связи AF.

Функция ограничения системы складывается из двух частей: цели и принуждающих связей.

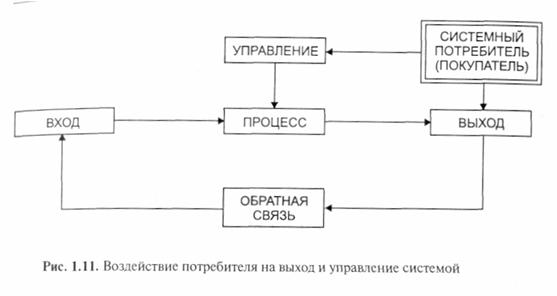
Ограничение системы является выходом органа, обозначаемого как потребитель (покупатель) выхода системы.

Системный потребитель (покупатель) воздействует на выход и управление системой, как это показано на рис. 1.11.

. Системные потребители (покупатели) существуют на всех уровнях действия подсистем. Требования к системе диктуются потребителем (покупателем) в форме ограничений.

Источник

Множество Т представляет собой множество некоторого (ко­нечного или бесконечного) интервала числовой оси. В этом слу­чае говорят, что система функционирует в непрерывном времени, например механические и электрические системы, системы, рас­сматриваемые в теории автоматического регулирования, и т. д.

Чтобы задать конкретный входной процесс x = L(t), достаточ­но указать соответствующее ему входное сообщение (t, x_l)_t.

Кроме того, множество <(t, x_L)_T> должно удовлетворять еще одному требованию, связанному с сочленением входных сообще­ний. Пусть (t, x_L1)_T и (t, x_L2)_T сообщения из множества <(t, x_L)_T>. Пусть, далее, t, t2 _t1 и(t, x_L2] t3 _T2. Совокупность упорядоченных пар (t*, х*), где

называется пространством выходных сигналов системы. По ана­логии с входным процессом введем понятие выходного процесса y=N(t), а также определим выходное сообщение (t, y_N)_T и его отрывок (t, y_N]_t1 t 2 на полуинтервале (t₁, t₂].

На этом можно считать исчерпанной формальную интерпре­тацию второго и третьего предположений о характере функци­онирования систем.

Глобальное состояние и глобальная реакция системы. Пусть для системы S множество ее состояний Z, а функция R: (X ´ Z) ® Y такова, что

Абстрактные линейные системы. Хотя многие понятия теории систем можно определить, опираясь исключительно на понятие общей системы (3.1), получение содержательных математических результатов становится возможным только после введения до­полнительных структур. Таким дополнительным понятием явля­ется понятие линейности систем.

s Î S и s’Î S Þ s + s’ Î S

s Î S и a Î A Þ a_x Î S

где «+» обозначает (внутреннюю) операцию сложения в X´Y, а через а_x, обозначен результат (внешней) операции умножения на скаляр. Тогда S называется (абстрактной) полной линейной системой.

В соответствии с современной терминологией алгеброй называют множество вместе с некоторыми конечными операциями, а линейной алгеброй, в частное внутренней и одной внешней операциями, удовлетворяющими аксиомам векторного пространства. Операция «+» и умножения на скаляр определяются на X´Y естественным образом:

В теории линейных систем фундаментальную роль играет следующая теорема.

1 1 Z есть линейная алгебра над А;

2 2 существует пара таких линейных отображений

что для всех (x,y) Î X´Y

Отображение R называют линейной глобальной реакцией системы тогда, и только тогда, когда

1 1 R согласуется с S, т.е.

2 2 Z является линейной алгеброй над полем А скаляров линейных алгебр X и У.

Существуют два таких линейных отображений R1: Z®Y и R2: X ®Y, что для любых (x,y) Î X´Y

Источник