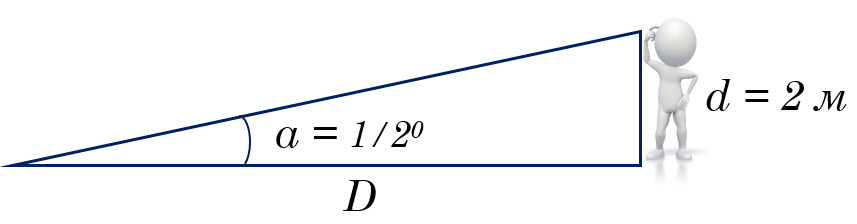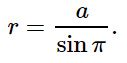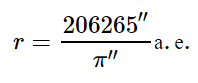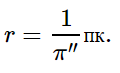Что называется угловым расстоянием в астрономии
УГЛОВОЕ РАССТОЯНИЕ
Смотреть что такое «УГЛОВОЕ РАССТОЯНИЕ» в других словарях:
Угловое расстояние — Длина дуги, выраженная в угловых единицах (т. е. в радианах, градусах, дуговых минутах или секундах), которая соответствует данному углу наблюдения. Например, угловое расстояние между двумя точками на небесной сфере представляет собой угол между… … Астрономический словарь
угловое расстояние — kampinis atstumas statusas T sritis Standartizacija ir metrologija apibrėžtis Atstumas, išreikštas kampo matavimo vienetais. atitikmenys: angl. angular distance vok. Winkelentfernung, f rus. угловое расстояние, n pranc. distance angulaire, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
угловое расстояние — kampinis atstumas statusas T sritis fizika atitikmenys: angl. angular distance; angular separation vok. Winkelentfernung, f rus. угловое расстояние, n pranc. distance angulaire, f … Fizikos terminų žodynas
Угловое разрешение — Разрешение способность оптического прибора измерять линейное или угловое расстояние между близкими объектами, показывать раздельно близко расположенные объекты. Содержание 1 Угловое разрешение 2 Линейное разрешение 3 Общие сведения … Википедия
угловое увеличением — 3.1 угловое увеличением (angular magnification M): Угловое увеличение М оптического прибора есть отношение угла наблюдения объекта, опирающегося на входной зрачок прибора (aприб), к углу наблюдения объекта глазом без прибора (aгл) Примечание В… … Словарь-справочник терминов нормативно-технической документации
ЗЕНИТНОЕ РАССТОЯНИЕ — угловое расстояние небесного светила или земного предмета от зенита. Обозначается г, отсчитывается вдоль круга высоты от 0 до 180°. С высотой h связано соотношением z = 90° h … Естествознание. Энциклопедический словарь
Зенитное расстояние — угловое расстояние небесного светила от зенита. Обозначается Z и отсчитывается вдоль круга высоты от 0 до 180˚. С высотой h связано соотношением Z = 90˚ h … Астрономический словарь
зенитное расстояние — угловое расстояние небесного светила или земного предмета от зенита. Обозначается z, отсчитывается вдоль круга высоты от 0 до 180º. С высотой h связано соотношением z = 90º – h. * * * ЗЕНИТНОЕ РАССТОЯНИЕ ЗЕНИТНОЕ РАССТОЯНИЕ, угловое расстояние… … Энциклопедический словарь
ПОЛЯРНОЕ РАССТОЯНИЕ — Расстояние между полюсом и данной точкой на земной поверхности. Объяснение 25000 иностранных слов, вошедших в употребление в русский язык, с означением их корней. Михельсон А.Д., 1865. ПОЛЯРНОЕ РАССТОЯНИЕ Угловое расстояние звезды от видимого… … Словарь иностранных слов русского языка
Угловое расстояние
Смотреть что такое «Угловое расстояние» в других словарях:
УГЛОВОЕ РАССТОЯНИЕ — УГЛОВОЕ РАССТОЯНИЕ, в астрономии расстояние на небесной сфере между двумя небесными телами, измеренное по дуге большого круга, проходящего через них, с наблюдателем в центре. Например, угловое расстояние между двумя звездами Большой Медведицы,… … Научно-технический энциклопедический словарь
угловое расстояние — kampinis atstumas statusas T sritis Standartizacija ir metrologija apibrėžtis Atstumas, išreikštas kampo matavimo vienetais. atitikmenys: angl. angular distance vok. Winkelentfernung, f rus. угловое расстояние, n pranc. distance angulaire, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
угловое расстояние — kampinis atstumas statusas T sritis fizika atitikmenys: angl. angular distance; angular separation vok. Winkelentfernung, f rus. угловое расстояние, n pranc. distance angulaire, f … Fizikos terminų žodynas
Угловое разрешение — Разрешение способность оптического прибора измерять линейное или угловое расстояние между близкими объектами, показывать раздельно близко расположенные объекты. Содержание 1 Угловое разрешение 2 Линейное разрешение 3 Общие сведения … Википедия
угловое увеличением — 3.1 угловое увеличением (angular magnification M): Угловое увеличение М оптического прибора есть отношение угла наблюдения объекта, опирающегося на входной зрачок прибора (aприб), к углу наблюдения объекта глазом без прибора (aгл) Примечание В… … Словарь-справочник терминов нормативно-технической документации
ЗЕНИТНОЕ РАССТОЯНИЕ — угловое расстояние небесного светила или земного предмета от зенита. Обозначается г, отсчитывается вдоль круга высоты от 0 до 180°. С высотой h связано соотношением z = 90° h … Естествознание. Энциклопедический словарь
Зенитное расстояние — угловое расстояние небесного светила от зенита. Обозначается Z и отсчитывается вдоль круга высоты от 0 до 180˚. С высотой h связано соотношением Z = 90˚ h … Астрономический словарь
зенитное расстояние — угловое расстояние небесного светила или земного предмета от зенита. Обозначается z, отсчитывается вдоль круга высоты от 0 до 180º. С высотой h связано соотношением z = 90º – h. * * * ЗЕНИТНОЕ РАССТОЯНИЕ ЗЕНИТНОЕ РАССТОЯНИЕ, угловое расстояние… … Энциклопедический словарь
ПОЛЯРНОЕ РАССТОЯНИЕ — Расстояние между полюсом и данной точкой на земной поверхности. Объяснение 25000 иностранных слов, вошедших в употребление в русский язык, с означением их корней. Михельсон А.Д., 1865. ПОЛЯРНОЕ РАССТОЯНИЕ Угловое расстояние звезды от видимого… … Словарь иностранных слов русского языка
Что называется угловым расстоянием в астрономии
Почему так трудно определить размеры небесных объектов и расстояния до них? Все дело в том, что размеры удаленных объектов мы можем определить только по сравнению размерами известных объектов, а на небе нам не с чем сравнивать. Мы видим на небе множество светящихся точек, но яркость точки может определяться как ее размером, абсолютной светимостью, так и расстоянием до нее.
Поэтому в астрономии практически невозможно определить оптическими методами линейный размер удаленного объекта, можно определить только его угловой размер.
Древние греки изобрели тригонометрию, которая позволяет определить количественные соотношения между углами, линейными размерами и линейными расстояниями. С помощью простых математических соотношений, включающих базовую тригонометрию, мы можем вычислить расстояния до удаленных объектов, размеры которых известны (или размеры, если расстояния известны).
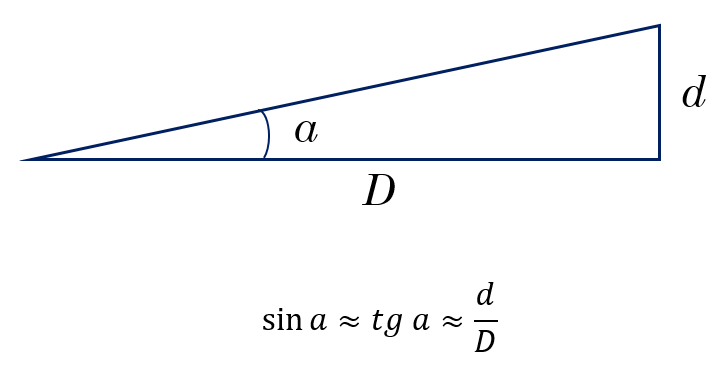
Уравнение малых углов
Если углы малые, то синус угла примерно равен тангенсу, который, в свою очередь примерно равен самому углу в радианной мере.
Уравнение малых углов включает в себя угловой размер объекта, его линейный размер и расстояние. Если известны какие-либо две из этих величин, можно вычислить третью. Обратимся к угловому размеру с символом a , выраженному в секундах дуги. Обозначим диаметр объекта как d , а расстояние до него как D . Тогда уравнение малого угла
a / 206 265 = d / D
Число 206 265 называется константой пропорциональности. Число 206 265 на самом деле является числом секунд дуги в угле 57,3° , который является специальным углом, называемым радианом. Радиан определяется как центральный угол дуги, длина которой равна радиусу окружности. Длина окружности равна 2πr , Радиан равен 360° / 2 π = 57,3° или около шестой части полного круга.
D = 206 265 d / a
Используя метрические единицы, найдем
D = (2.1 x 10 5 x 2) / (1.8 x 10 3 ) = 2.3 х 10 2 метра = 230 метров
Если ваш друг имеет рост 2 метра и угловой размер его составляет ½ ° (или 1800 угловых секунд), расстояние D составляет 230 метров. Обратите внимание, что мы округляем все наши оценки до двух значащих цифр, потому что измерение угла вряд ли будет очень точным.
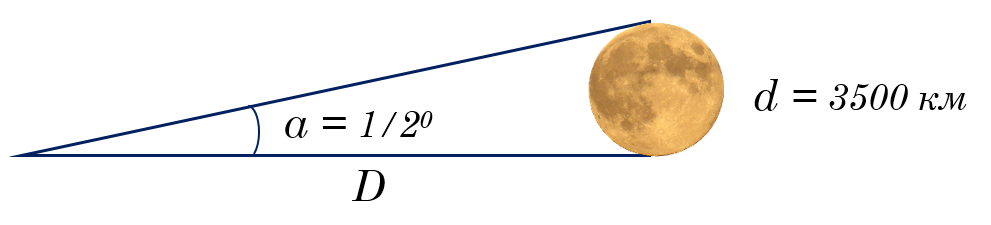
Как поняли древние греки, уравнение малого угла можно использовать для определения астрономических расстояний. Они не могли точно измерить диаметр Луны, но они знали ее угловой размер a, который также составляет примерно ½° , или 1800″ .
Если мы используем современные знания о том, что диаметр Луны составляет около 3500 километров, мы можем оценить расстояние до нее так же, как мы это сделали для расстояния друга выше. В метрических единицах d будет 3,5 × 10 6 метров. Уравнение будет гласить:
D = (2.1 × 10 5 × 3.5 × 10 6 ) / (1.8 × 10 3 ) ≈ 4 х 10 8 метров ≈ 4 x 10 5 километров.
Реальное среднее расстояние до Луны 384 000 км. Неплохая точность!
Методы определения расстояний до звезд
Годичный параллакс
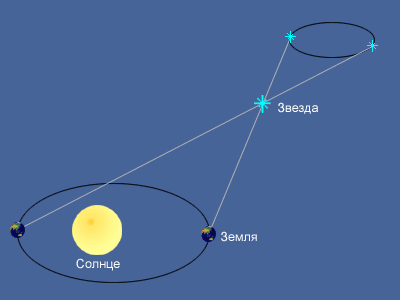
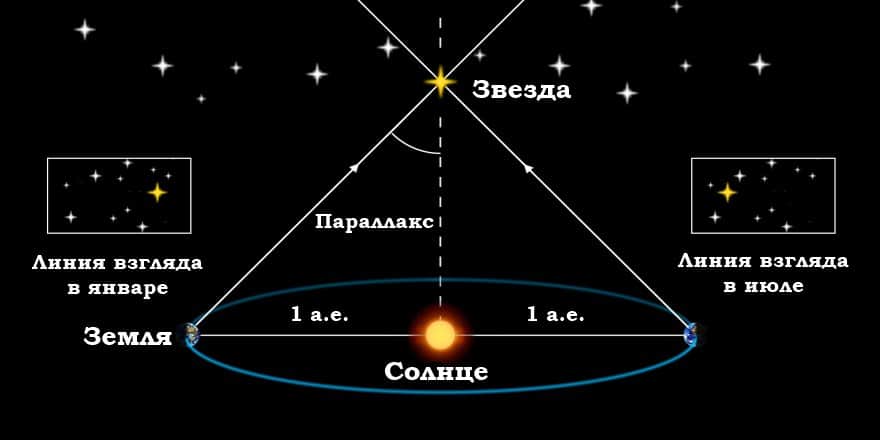
Кажущееся перемещение более близкой звезды на фоне очень далеких звезд происходит по эллипсу с периодом в 1 год и отражает движение наблюдателя вместе с Землей вокруг Солнца. Маленький эллипс, описываемый звездой, называется параллактическим эллипсом. В угловой мере большая полуось этого эллипса равна величине угла, под которым со звезды видна большая полуось земной орбиты, перпендикулярная направлению на звезду. Этот угол называется годичным параллаксом ( π ).
Параллактические смещения звезд служат неопровержимым доказательством обращения Земли вокруг Солнца. Расстояния до звезд определяются по их годичному параллактическому смещению, которое обусловлено перемещением наблюдателя (вместе с Землей) по земной орбите.
1 пк = 206 265 а. е. = 3,086 · 10 13 км.
Таким образом, расстояние до звезд в парсеках будет определяться выражением
В астрономических единицах обычно выражаются расстояния до тел Солнечной системы. Расстояния до небесных тел, находящихся за пределами Солнечной системы, обычно выражаются в парсеках, килопарсеках ( 1 кпк = 10 3 пк ) и мегапарсеках ( 1 Мпк = 10 6 пк ), а также в световых годах ( 1 св. г. = 9,46 · 10 12 км = 63 240 а. е. = 0,3067 пк или 1 пк = 3,26 св. г. ).
Фотометрический метод определения расстояний
Для светил, у которых известны тригонометрические параллаксы, можно, определив M по этой же формуле, сопоставить физические свойства с абсолютными звездными величинами. Это сопоставление показало, что абсолютные звездные величины многих классов светил (звезд, галактик и др.) можно оценивать по ряду их физических свойств.
Цефеиды (стандартные свечи)
Для долгопериодических цефеид (периоды колебаний от 1 до 146 сут.), относящихся к звездному населению I типа (плоской составляющей Галактики), установлена важная зависимость период-светимость, согласно которой, чем короче период колебаний блеска, тем цефеида слабее по абсолютной величине. С помощью этой зависимости можно определить абсолютные величины цефеид по длительности их периодов колебаний блеска и, следовательно, фотометрические расстояния до цефеид и звездных скоплений, спиральных рукавов и звездных систем, где они наблюдаются (см. Период-светимость зависимость). Погрешность определения расстояний по цефеидам составляет для звездных скоплений в среднем 40% (в отдельных случаях меньше).
При тестировании программы расчета углового расстояния между двумя точками на небесной сфере обнаружилось, что представленное здесь расчетное табло позволяет пересчитывать время из представления в часах, минутах и секундах в десятичные доли часа и наоборот, а угловые величины пересчитывает из дробно-десятичного формата в градусах в формат: градусы, минуты, секунды
Расчет углового расстояния между двумя объектами (звездами) небесной сферы
Координаты небесного
Объекта 1
Угловое расстояние между объектами
Координаты небесного
Объекта 2
Что-то пошло не так.
Итоговый отчет
Oбъект 1: Регул (10ч 08м 22с; 11° 58′ 12″);
Созвездие: Leo, Лев (Leo)
Расчет углового расстояния между двумя астрономическими объектами, положение которых определено во второй экваториальной системе координат
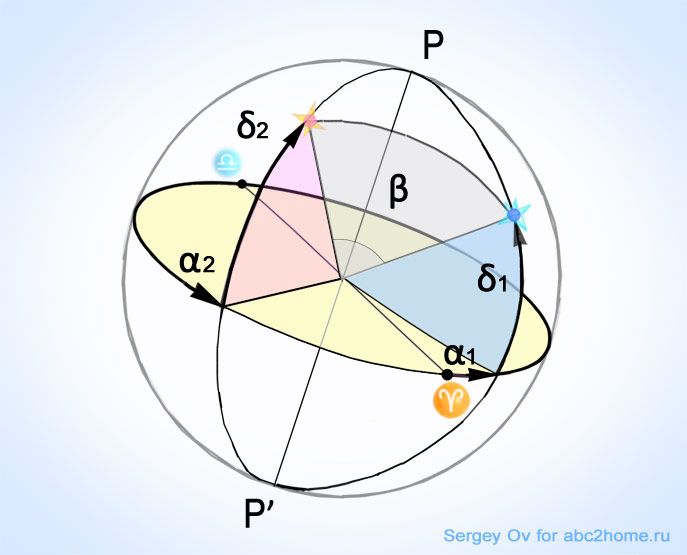
Во второй экваториальной системе координат положение объектов определяется двумя угловыми параметрами, называемыми прямое восхождение α и склонение δ (Рис.1).
Рис. 1. Небесная сфера, угловое расстояние β между двумя точками на сфере и их угловые экваториальные координаты
при использовании численных методов, важно помнить что arccos(x)=0 при x=1, во избежание деления на 0.
Примечательные угловые расстояния
Развеиваем мифы
(нет в мире совершенства)
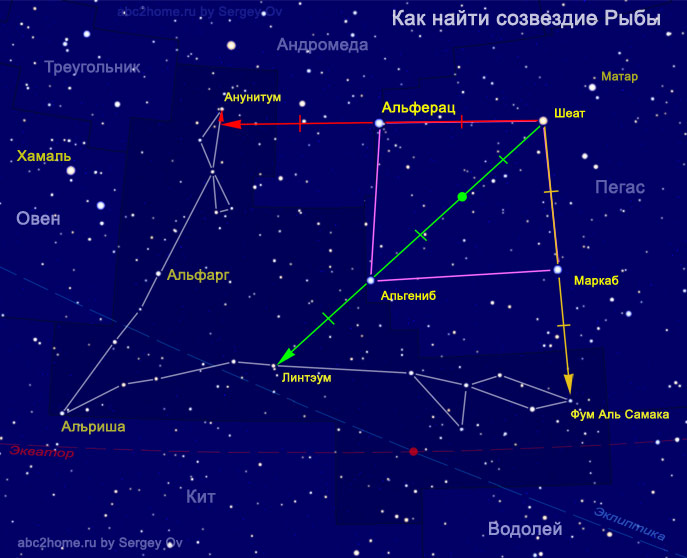
На данный момент на сайте нет детального описания древнейшего астеризма Большой Квадрат, но иллюстрация с его довольно крупным изображением есть:
Рис. 2. Как найти созвездие Рыбы с помощью астеризма Большой Квадрат
Как видно из рисунка Большой Квадрат, на самом деле, по конфигурации наиболее близок к трапеции. Для представленных далее астеризмов сезонных Треугольников на сайте имеется хоть какое-то писание и иллюстрации, поэтому для желающих ознакомиться с этими звездными объектами расставлены ссылки на страницы с их изображениями.
P.S. На этой странице используется Бета версия программы расчета между двумя небесными объектами, об обнаруженных недочетах, а так же возможных пожеланиях просьба сообщить на форум сайта (окно для входа на форум находится в нижней части страницы).
1. Эфемеридами называются рассчитанные наперед угловые координаты небесных тел. если подходить к современному понятию строго, то ЭФЕМЕР́ИДЫ (астрономический термин), координаты небесных светил и др. переменные астрономические величины, вычисленные для ряда последовательных моментов времени и сведенные в таблицы.
Большой российский энциклопедический словарь. 2012
Что такое градусы, угловые минуты и угловые секунды?
Как небесные наблюдатели измеряют расстояния в ночном небе? И как это понимать, когда они говорят об объектах, находящихся на расстоянии нескольких градусов (или нескольких угловых минут или угловых секунд) друг от друга.
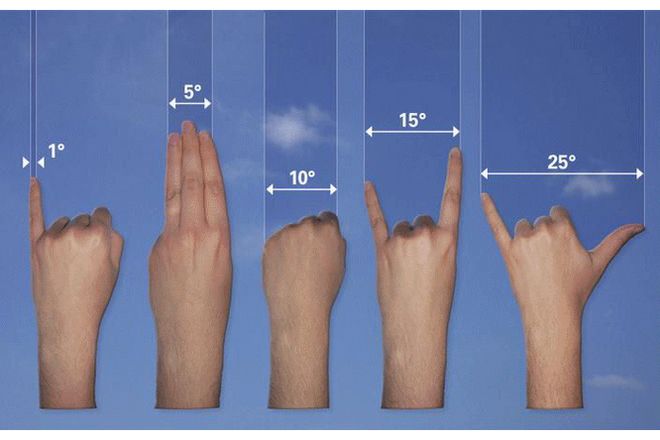
Самый удобный измерительный прибор для измерения небесного свода всегда с вами, на конце вашей руки.
Вы можете использовать ширину вашего мизинца, кулака и расстояние между пальцами руки. Чтобы измерить расстояние между небесными объектами.
Это очень удобно, когда вы наблюдаете за планетами и звездами, или планетами, звездами и Луной. А также другими космическими объектами.
Вы часто обнаружите, что эти объекты описываются как находящиеся на некотором расстоянии друг от друга в градусах, дуговых минутах или дуговых секундах.
Насколько это далеко друг от друга?
Начнем с того, что от одной стороны неба до другой горизонт измеряется 180 градусами, или полукругом. Поэтому от горизонта до зенита, точки прямо над головой, должно быть 90 градусов. Если вы находитесь на ровной местности с ровным горизонтом. А не в холмистом или горном районе.
“подручное”средство для измерения градусов на небосводе. Изображение Астрономического общества Форт-Уэрта
Общее правило астрономов-любителей состоит в том, что ширина вашего кулака, удерживаемого на расстоянии вытянутой руки, равна примерно 10 градусам. Вы можете смотреть на свой кулак и кулак маленького ребенка и удивляться. Как оба могут измерять 10 градусов, но размер кулаков людей обычно пропорционален длине их рук. Таким образом, ребенок с маленьким кулаком и маленькой рукой будет измерять приблизительно 10 градусов с их точки зрения. Так же как взрослый с большим кулаком и более длинной рукой измеряет 10 градусов с их точки зрения.
Если вы хотите сделать грубую проверку, вытяните руку и кулак к горизонту. Затем положите вторую руку и кулак поверх первой и чередуйте, стараясь не раскачиваться, пока не насчитаете девять кулаков. Ваш девятый кулак должен быть направлен прямо вверх.
Для градусов меньше 10 вам будет достаточно только пальцев. На расстоянии вытянутой руки мизинец измеряет от 1 до 1,5 градусов. А три средних пальца около 5 градусов. Для больших углов вам нужно будет раздвинуть пальцы. Чтобы найти 15 градусов, используйте указательный палец и мизинец, разведенные в стороны. А чтобы найти 25 градусов, посмотрите на промежуток между мизинцем и большим пальцем, разведенными в стороны.
Большая Медведица – хороший пример для проверки ваших измерений
Последние две звезды в чаше, те, которые используются для поиска полярной звезды. Они находятся примерно в 5 градусах друг от друга. Две верхние звезды в чаше Большой Медведицы находятся на расстоянии 10 градусов друг от друга. И, наконец, используя ту же самую далекую звезду в чаше Большой Медведицы, которую вы использовали для первых двух тестов плюс конечную звезду в ручке, вы отмерите 25 градусов.
Как вы думаете, насколько широко выглядит полная луна – сколько градусов она занимает? 5 градусов? Большинство людей переоценивают его размеры. Но на самом деле полная луна имеет всего пол-градуса в поперечнике.
А как насчет солнца? Хотя инстинктивно вы можете сказать, что солнце больше. Потому что его фактический размер огромен, если поставить его рядом с Луной. Однако площадь, которую занимают солнце и луна, равно полу-градусу. Вы можете догадаться об этом, даже не проверяя солнце с помощью ваших мизинцевых измерений. Потому что вы наверняка знаете, что во время полных солнечных затмений луна временно скользит прямо перед солнцем. Блокируя весь его свет на несколько коротких минут.
Теперь, когда у вас есть представление о градусах. Если вы хотите оценить меньшие расстояния, вам нужно знать, что градусы далее делятся на минуты. В 1 градусе 60 угловых минут, поэтому и луна и солнце имеют 30 угловых минут в поперечнике. Угловые минуты также можно разделить. 60 угловых секунд составляют 1 угловую минуту.
Возвращаясь к Большой Медведице, звезды в изгибе ручки представляют собой двойную звездную систему под названием Мицар и Алькор. Они разделены всего 12 дуговыми минутами. Люди с хорошим зрением могут видеть две отдельные звезды без помощи оптических приборов. У Мицара есть еще один спутник, который еще ближе, чем Алькор. Двойная звезда Мицара находится всего в 14,4 угловых секундах. Минуты угла записываются символом ( ‘ ), а секунды записываются символом ( ” ).
Вы можете сказать, сколько времени до захода солнца, измерив его расстояние от горизонта. Солнце движется по небу примерно на 15 градусов за час. Движение на 15 градусов в час в течение 24 часов будет равно 360 градусам, или целому дню от заката до заката.
закат над Тадж-Махалом, фото Абхинав Сингхай
Конечно, солнце на самом деле не движется. Это только кажется, что оно движется в небе. Помните, что если вы не находитесь на экваторе, солнце не движется прямо к горизонту. Солнце опускается вниз под углом, который становится круче, чем ближе вы находитесь к полюсам.
Градусы, угловые минуты и угловые секунды, все это полезные единицы измерения в астрономии. Иногда даже ваша собственная рука может вам помочь произвести измерения помочь.