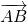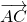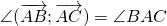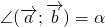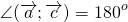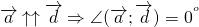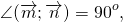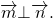Что называется углом между векторами
Угол между векторами
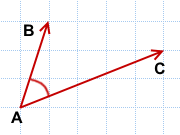
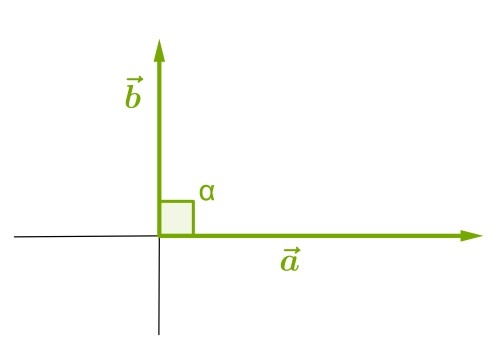
1) Углом между векторами
называется угол BAC:
2) Углом между двумя ненулевыми векторами называется угол между векторами, равными данным и имеющими общее начало.
Поскольку нулевой вектор считается коллинеарным любому вектору, если один из векторов нулевой либо если оба вектора нулевые, то и в этом случае угол между векторами равен 0°.
Угол между равными векторами также равен 0°.
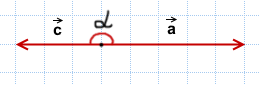
Угол между противоположно направленными векторами равен 180°.
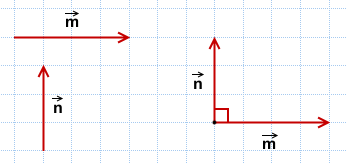
Если угол между векторами равен 90°, то такие векторы называются перпендикулярными.
Рассмотрим понятие угла между векторами на конкретных примерах.
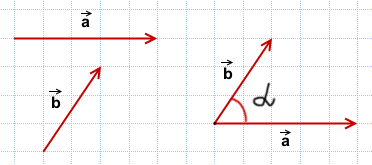
Определить угол между векторами:
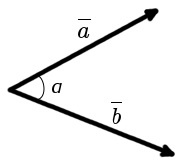
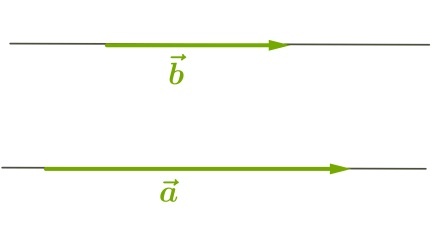
1) Данные векторы не сонаправлены.
Выберем некоторую точку и от неё отложим векторы, равные данным.
Угол между ними равен α.
Значит, и угол между данными векторами равен α.
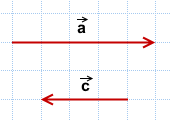
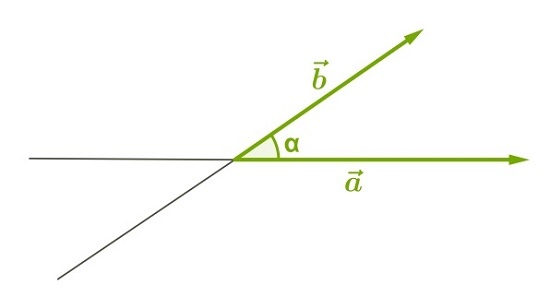
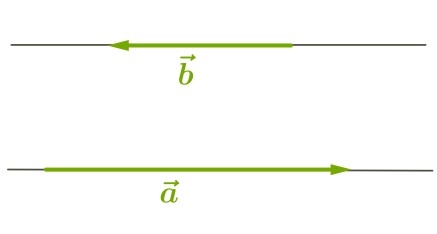
2) Данные векторы противоположно направлены.
Значит, угол между ними равен 180°:
Проиллюстрируем этот результат, отложив векторы, равные данным, от одной точки:
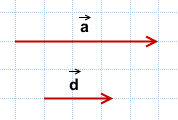
4) Отложим данные векторы от общего начала.
Так как угол между ними равен 90°:
Угол между векторами можно найти с помощью их скалярного произведения.
Как найти угол между векторами
Угол между векторами
Угол между векторами — это угол между отрезками, которые изображают эти две направляющие и которые отложены от одной точки пространства. Другими словами — это кратчайший путь, на который можно повернуть один из векторов вокруг его начала до положения общей направленности со вторым.
На изображении это α, который также можно обозначить следующим образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как и любой другой угол, векторный может быть представлен в нескольких вариациях.
Острый:
Тупой:
Прямой:
С величиной \(0^\circ\) (то есть, векторы сонаправлены):
С величиной \(180^\circ\) (векторы направлены в противоположные стороны):
Нахождение угла между векторами
Как правило, угол между \( \overrightarrow a\) и \(\overrightarrow b\) можно найти с помощью скалярного произведения или теоремы косинусов для треугольника, который был построен на основе двух этих направляющих.
Скалярное произведение — это число, которое равно произведению двух направляющих на косинус угла между ними.
Формула скалярного произведения:
\(\left(\overrightarrow a;\overrightarrow b\right)=\left|\overrightarrow a\right|\times\left|\overrightarrow b\right|\times\cos\left(\widehat<\overrightarrow a;\overrightarrow b>\right)\)
В случае, если \overrightarrow a и \overrightarrow b не нулевые, можно найти косинус α между ними, опираясь на формулу:
Расчет угла, если вектор задан координатами
Если же координаты находятся в трехмерном пространстве и заданы в виде:
то формула принимает такой вид:
Расчет угла, если заданы три точки в прямоугольной системе координат
В этом случае проще будет разобраться с объяснениями сразу на примере.
Решение
Для начала найдем их координаты по известным координатам заданных точек:
После этого уже можем применить формулу для определения косинуса угла на плоскости и подставить известные значения:
Примеры решения задач
Для наглядности, взглянем на примеры решения задач по данной теме.
Задача 1
Решение
Подставим известные значения:
Далее найдем угол между данными векторами:
Задача 2
Решение
Используем формулу для нахождения косинуса угла между направляющими в трехмерной системе координат:
Подставляем значения и получаем:
Теперь находим угол α:
Задача 3
Угол между векторами.
 |
Формула вычисления угла между векторами
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| | a | · | b | | 5 · 5 | 25 |
Решение: Найдем скалярное произведение векторов:
a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.
Найдем модули векторов:
| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| | a | · | b | | 5√ 2 · 5√ 2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| | a | · | b | | 5 · 6 | 15 |
Решение: Найдем скалярное произведение векторов:
a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.
Найдем модули векторов:
| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Как найти угол между векторами
Вы будете перенаправлены на Автор24
Угол между векторами
Для того, чтобы мы могли ввести формулу для вычисления угла между векторами через координаты, нужно сначала разобраться с самим понятием угла между этими векторами.
Рисунок 1. Угол между векторами. Автор24 — интернет-биржа студенческих работ
Нахождение угла между векторами в пространстве с помощью скалярного произведения
Вспомним сначала, что называется скалярным произведением и каким образом его можно находить.
Скалярным произведением двух векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.
Математически это может выглядеть следующим образом:
Также, помимо того, как из самого определения 1, для нахождения скалярного произведения можно пользоваться следующей теоремой.
Математически выглядит следующим образом
$\overline<δ>\cdot \overline<β>=δ_1 δ_2+β_1 β_2+γ_1 γ_2$
Готовые работы на аналогичную тему
Найдя значение косинуса, мы легко найдем и значение самого угла.
Решение.
Найдем скалярное произведение между данными векторами через координаты:
$\overline<δ>\cdot \overline<β>=1\cdot 3+(-2)\cdot 0+2\cdot 4=11$
Найдем длины этих векторов:
В результате, получим
Нахождение угла между векторами с помощью векторного произведения
Вспомним сначала, определение векторного произведения и каким образом его можно находить.
Векторным произведением двух векторов называется такой вектор, который будет перпендикулярен обоим данным векторам, и его длина равна произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют ту же ориентацию, как и декартова система координат.
Математически это выглядит следующим образом:
Рисунок 2. Векторное произведение. Автор24 — интернет-биржа студенческих работ
Для нахождения вектора векторного произведения можно пользоваться следующей формулой:
Найдем вектор векторного произведения по формуле:
$\overline<δ>х\overline<β>=\begin
Найдя значение синуса, мы легко найдем и значение самого угла между векторами через координаты через формулу.
Решение.
Найдем вектор векторного произведения между данными векторами по формуле:
Найдем длины этих векторов:
В результате, получим
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 20 07 2021
Вектор. Скалярное произведение векторов. Угол между векторами.
Скалярным произведением (или внутренним произведением) 2 векторов есть операция с двумя
векторами, итогом чего является число (скаляр), которое не зависит от системы координат и которое
характеризует длины векторов-сомножителей и угол между векторами.
Также скалярным произведением двух векторов называется число, которое
равно произведению модулей 2 векторов на косинус угла между векторами.
Скалярное произведение векторов формула:

Этой операции соответствует умножение длины вектора x на проекцию вектора y на вектор x. Эта
операция зачастую рассматривается как коммутативная и линейная по каждому из сомножителей.
Скалярное произведение векторов 



значения, т.е. 
Еще используются такие обозначения: 


В основном имеется ввиду, что скалярное произведение определено положительно, т.е.
при каждом 
(неопределенным).
Если хотя бы один из 2 векторов 


Свойства скалярного произведения векторов.
1. 
2. 

3. Если 
4. Если и 



5.
6.
7.
Если же векторы 



произведение векторов, формула:
Формула для определения длины вектора:
Длина (модуль) вектора, с известными координатами, равен квадратному корню из суммы квадратов
Длина вектора 
Как определить угол между 2 векторами:
Как найти угол между двумя векторами 

Ежели угол меж двумя векторами острый, то их скалярное произведение имеет положительный знак; если
же угол между двумя векторами тупой, то их скалярное произведение имеет отрицательный знак.
Скалярное произведение двух ненулевых векторов равно нулю, тогда и только тогда, когда эти векторы
ортогональны.
Альтернативное определение скалярного произведения векторов (вычисление скалярного
произведения двух векторов, заданных своими координатами).
Вычислить координаты вектора, если заданы координаты его начала и его конца очень просто. Давайте
рассмотрим этот вопрос:
Исходя из этого, координаты вектора АВ:
Точно так же и в двухмерном пространстве – разница в отсутствии третьих координат.
Итак, предположим, даны два вектора, которые заданы набором координат своих точек:
а) В двухмерном пространстве (плоскость):
Значит, скалярное произведение этих векторов вычислим по формуле:
б) В трехмерном пространстве:
Как и в двухмерном случае, скалярное произведение двух векторов вычисляем по формуле: