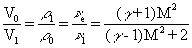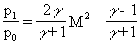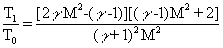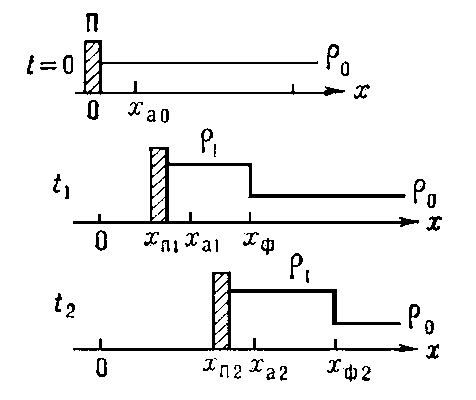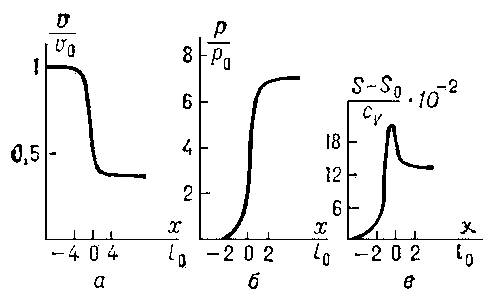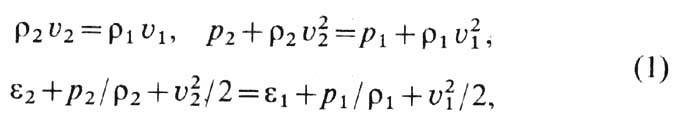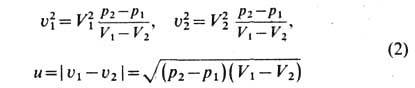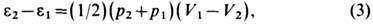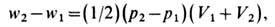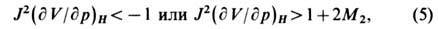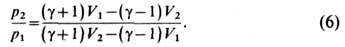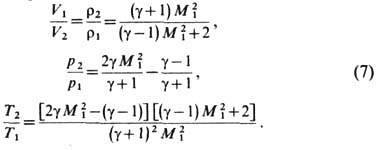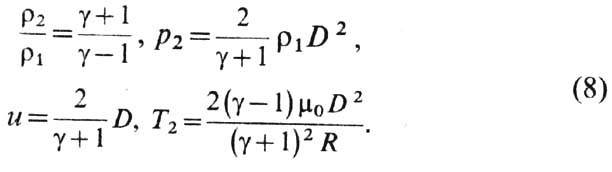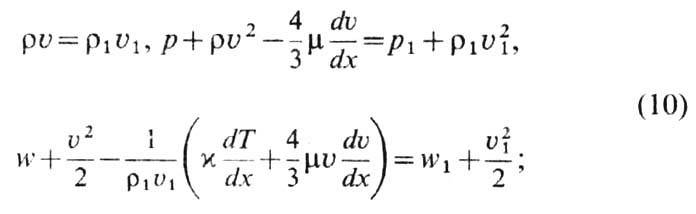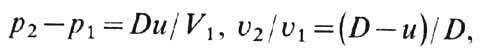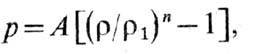Что называется ударной волной
Ударная волна
Полезное
Смотреть что такое «Ударная волна» в других словарях:
УДАРНАЯ ВОЛНА — (скачок уплотнения), распространяющаяся со сверхзвуковой скоростью тонкая переходная область, в к рой происходит резкое увеличение плотности, давления и скорости в ва. У. в. возникают при взрывах, детонации, при сверхзвуковых движениях тел, при… … Физическая энциклопедия
ударная волна — Распространяющаяся со сверхзвуковой скоростью переходная область в газе, жидкости или в твердом теле, в которой происходит резкое увеличение плотности, давления и скорости среды [ГОСТ 26883 86] [ГОСТ Р 22.0.08 96] ударная волна Ударная волна,… … Справочник технического переводчика
УДАРНАЯ ВОЛНА — распространяющаяся со сверхзвуковой скоростью тонкая переходная область, в которой происходит резкое увеличение плотности, давления и температуры вещества. К наиболее характерным случаям относятся ударные волны, возникающие при взрывах, полете… … Большой Энциклопедический словарь
УДАРНАЯ ВОЛНА — процесс распространения скачка уплотнения в среде (в грунте, воздухе или воде) со скоростью, превышающей скорость звука в той же среде. Поверхность, отделяющая сжатую среду от невозмущённой, К ст. Ударная волна Распространение звуковых волн и… … Большая политехническая энциклопедия
Ударная волна — распространяющаяся со сверхзвуковой скоростью в сжимаемой среде тонкая переходная область, в которой происходит резкое увеличение давления р, плотности (ρ), энтропии, скорости среды и др. газодинамических переменных. В механике сплошных сред эту… … Энциклопедия техники
Ударная волна — см. Взрывная волна. Горная энциклопедия. М.: Советская энциклопедия. Под редакцией Е. А. Козловского. 1984 1991 … Геологическая энциклопедия
УДАРНАЯ ВОЛНА — распространяющаяся со сверхзвуковой скоростью тонкая переходная область, в которой происходит резкое увеличение плотности, давления и температуры вещества. У. в. возникает при взрывах (см. Взрывная волна), полете тел со сверхзвуковой скоростью, в … Российская энциклопедия по охране труда
УДАРНАЯ ВОЛНА — УДАРНАЯ ВОЛНА, в текучих средах (жидкостях или газах) быстро перемещающаяся в пределах среды область, характеризующаяся резким перепадом давления и плотности. Ударные волны возникают при движении объектов со сверхзвуковыми скоростями. Т. к.… … Научно-технический энциклопедический словарь
Ударная волна — распространяющаяся со сверхзвуковой скоростью в газе, жидкости или твердом теле область, в которой происходит резкое увеличение плотности, давления и скорости среды. У.в. при взрыве может поражать людей и животных, разрушать сооружения,… … Словарь черезвычайных ситуаций
Ударная волна — Течение жидкостей и газа Ползучее течение Ламинарное течение Потенциальное течение Отрыв течения Вихрь Неустойчивость … Википедия
ударная волна — распространяющаяся со сверхзвуковой скоростью тонкая переходная область, в которой происходит резкое увеличение плотности, давления и температуры вещества. К наиболее характерным случаям относятся ударные волны, возникающие при взрывах, полёте… … Энциклопедический словарь
УДАРНАЯ ВОЛНА
— движущаяся по веществу поверхность разрыва непрерывности скорости течения, давления, плотности и др. величин. У. в. возникают при взрывах, детонации, при сверхзвуковых движениях тел (см. Сверхзвуковое течение), при мощных электрич. разрядах и т. д. Напр., при воздушном взрыве взрывчатых веществ (BB) образуются высоконагретые продукты, находящиеся под большим давлением. Продукты взрыва под действием давления расширяются, приводя в движение и сжимая сначала ближайшие, а затем всё более далёкие слои воздуха. Поверхность, к-рая отделяет сжатый воздух от невозмущённого, представляет собой У. в.
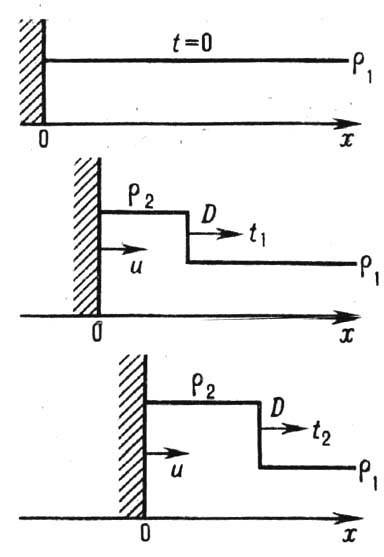
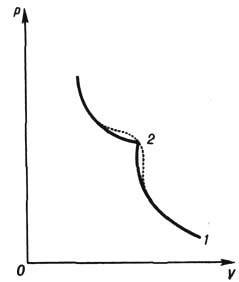
Простейший пример возникновения и распространения У. в.- сжатие газа в трубе поршнем. Если первоначально покоившийся поршень мгновенно приходит в движение с пост. скоростью и, то сразу же непосредственно перед ним возникает У. в. Скорость её распространения D по невозмущённому газу постоянна и больше и. Поэтому расстояние между поршнем и У. в. увеличивается пропорц. времени движения. Скорость газа за У. в. совпадает со скоростью поршня (рис. 1). Если поршень разгоняется до скорости и постепенно, то У. в. образуется не сразу. Вначале возникает волна сжатия с непрерывным распределением плотности и давления. С течением времени крутизна волны сжатия нарастает, т. к. возмущения от ускоряемого поршня догоняют её и усиливают, приводя в итоге к разрыву непрерывности всех гидродинамич. величин и к образованию У. в. (см. базовая динамика).
Рис. 1. Распределения плотности r в последовательные моменты времени t = 0, t 1 , t 2 в ударной волне, возбужда емой поршнем, движущимся с постоянной скоростью и (D- скорость ударной волны; D>u).
к-рые выражают законы сохранения массы, импульса и энергии. Индексы 1 и 2 относятся соответственно к величинам перед У. в. и за ней. Кроме того, величины Е, р и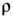 
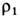
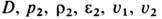
связаны уравнением состояния. Скорость распространения У. в. по невозмущённому веществу равна 
Т. о., при заданных параметрах вещества перед волной Р 1 . и 
шесть величин:
связаны пятью ур-ниями, т. е. У. в. при заданных р 1 и r 1 характеризуется всего одним независимым параметром, напр. D или р 2. , через к-рый могут быть выражены все остальные величины.
Интенсивность У. в. обычно характеризуют относительным скачком давления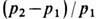 
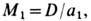
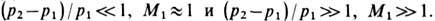
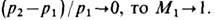
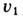
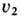
или Маха числом 
где 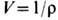a 1 —скорость звука в веществе перед У. в. Для У. в. малой и большой интенсивности соответственно 
Если
Из системы (1) получаются следующие выражения для 
и 
и для скорости течения и относительно вещества перед У. в. (скорость газа в лаб. системе координат на рис. 1):
(где 
—уд. объём), а также соотношение
к-рое наз. ур-нием ударной адиабаты (УА) или адиабаты Гюгоньо. Др. форма записи ур-ния УА эквивалентна (3):
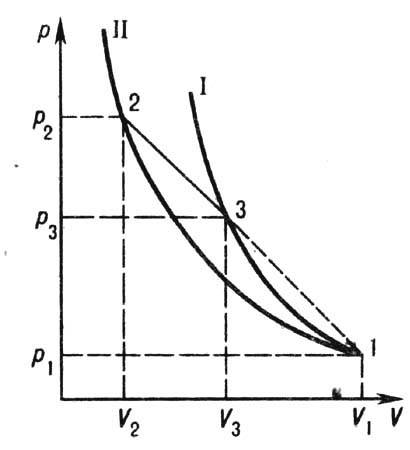
Рис. 2. Ударная адиабата (УА) с изломом или с перегибом (штриховая линия в точке 2); р, V—давление и объём вещества. Точка 1 соответствует состоянию вещества перед ударной волной.
Нарушение этих условий встречается редко и связано с наличием на УА изломов или перегибов (рис. 2), возможных при фазовых переходах в твёрдых телах (плавление, полиморфные превращения и др.) или при их пластич. деформациях, а также в газах в окрестностях критич. точки (Я. Б. Зельдович, 1946). С точностью до существования таких «аномалий» УА справедлива теорема Цемплена (1905), согласно к-рой возможны только У. в. сжатия. При указанных «аномалиях» УА в соответствии с теоретич. предсказаниями У. в. разрежения были получены экспериментально.
У. в. движется по исходному веществу со сверхзвуковой скоростью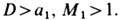 
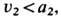
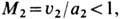
Поэтому газодинамич. возмущения из области за У. в. не проникают в вещество перед ней и не влияют, следовательно, на его состояние. Скорость У. в. относительно вещества за ней дозвуковая,
благодаря чему пространственное распределение газодинамич. величин за У. в. влияет на зависимость её интенсивности от времени. Напр., возмущения от ускоряющегося поршня, к-рый сжимает в трубе газ и создаёт У. в., догоняют и усиливают У. в. Приращение энтропии в У. в. малой интенсивности — величина третьего порядка малости, поэтому такую У. в. можно считать изэнтропичной. При неогранич. возрастании интенсивности У. в. сжатие, т. е. отношение 
остаётся ограниченным.
Устойчивость У. в. как гидродинамич. разрыва нарушается в случаях ур-ний состояния очень специального вида, приводящих к таким аномалиям формы УА (С. П. Дьяков, 1954), к-рые выражаются в виде неравенств
где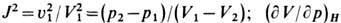 
—производная вдоль УА. В случае первого из неравенств (5), выполняющегося на УА с изломами и перегибами типа изображённых на рис. 2, У. в. расщепляется на конфигурацию из двух или большего числа волн. Веществ с такими ур-ниями состояния, при к-рых УА удовлетворяла бы второму из неравенств (5), по-видимому, не существует, хотя соответствующие ур-ния состояния и не запрещены термодинамически.
У. в. в газах. Формулы для У. в. имеют особенно простой вид в случае газа с пост, теплоёмкостью, т. е. когда
—отношение теплоёмкостей при пост, давлении и объёме (показатель адиабаты), R— газовая постоянная; m 0 — относит, мол. масса, Т—темп-pa. В этом случае ур-ние УА выражается в явном виде:
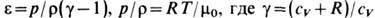
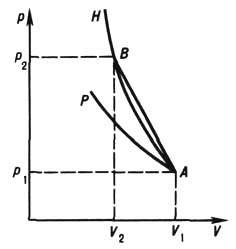
По сравнению с обычной адиабатой (адиабатой Пуассона), для к-рой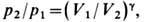 
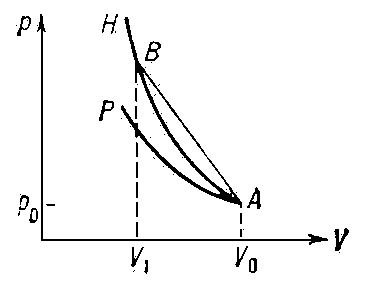
УА характеризуется большим возрастанием давления при сжатии (рис. 3).
Рис. 3. Ударная адиабата H и адиабата Пуассона Р, проходящие через общую точку А начального состояния ( В— точка конечного состояния УА).
Это является следствием необратимости нагрева газа в У. в. Параметры газа за У. в., отнесённые к их значениям перед У. в., выражаются через М 1 :
В пределе больших интенсивностей, т. е. при 
T. о., сколь угодно интенсивная У. V (меньше g). Напр., для одноатомного газа g = 5/3, h= 4, для двухатомного, напр. для воздуха, g = 7/5, h= 6. Однако ф-лы (6)-(8) имеют ограниченную применимость даже для идеального, т. е. достаточно разреженного газа (хотя и очень полезны при оценках и выявлении качественных закономерностей). В газе при высоких темп-pax происходят диссоциация молекул, хим. реакции, ионизация, что связано с затратами энергии, изменением теплоёмкости и числа частиц. При этом e сложным образом зависит от р и V. Если эта зависимость (ур-ние состояния) известна, то параметры газа за У. в. можно найти путём численного решения ур-ний (1)-(3).
Структура У. в. У. в., рассматриваемая в гидродинамике как разрыв, в действительности представляет собой переходный слой конечной протяжённости, к-рую называют ш и р и-н о й У. в. В нём происходят необратимые процессы перехода вещества из нач. состояния перед У. в. в конечное состояние за ней. В плотных газах ширина У. в. обычно пренебрежимо мала по сравнению с характерными размерами областей непрерывного течения по обе стороны У. в. Но в разреженных газах нередки случаи, когда это не так. Напр., на больших высотах в атмосфере У. в., движущаяся перед сверхзвуковым летательным аппаратом, может иметь ширину, сравнимую с расстоянием от начала переходного слоя до поверхности аппарата. Это необходимо учитывать при расчётах аэродинамики и температурного режима на поверхности.
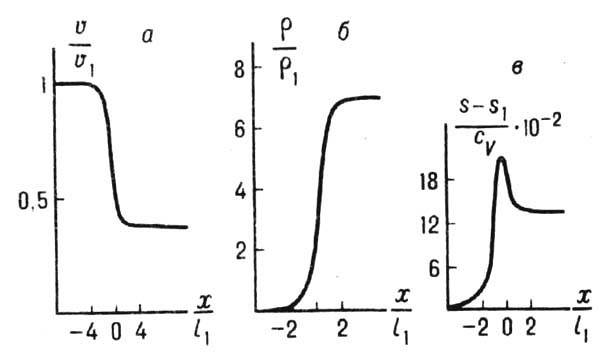
Рис. 4. Распределения скорости ( а), давления ( б), энтропии ( в) в вязком скачке уплотнения (СУ) с числом M 1 =2в газе с g = 7/5 и коэффициентом вязкости, не зави сящим от температуры; l 1 — длина свободного пробега молекул.
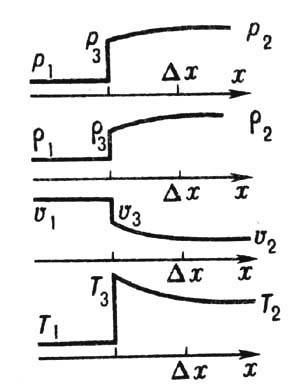
Релаксационная зона. В релаксац. зоне величины р,r, T, uизменяются только потому, что меняется ур-ние состояния, т. к. нек-рые его параметры «релаксируют», в результате чего уд. внутр. энергия зависит от времени t явно:
Рис. 6. Распределение давления р, плотносги r, скорости газа u и температуры T в релаксационной зоне ударной волны, распространяющейся по газу с замедленным воз буждением части степеней свободы.
Одномерное стационарное течение в релаксац. зоне может быть неустойчиво относительно турбулизации, подобно процессам в структуре детонац. волны (см. Детонация). Однако для этого необходимо сочетание редко (в отличие от детонац. волн) выполняемых в У. в. условий-наличия большого периода индукции в релаксац. зоне и затем быстрой релаксации.
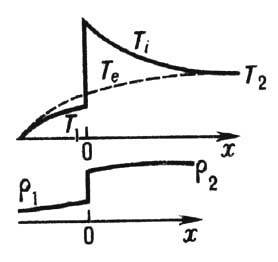
У. в. в плазме. Когда У. в. большой интенсивности распространяется по ионизованному газу, в СУ электронный газ сам по себе (т. е. при электрон-электронных столкновениях) нагревается значительно слабее ионного, т. к. в системе координат, где У. в. покоится, втекающие в неё электроны обладают ничтожной кинетич. энергией. Больший, но тоже малый по отношению к ионам нагрев электронного газа в СУ происходит за счёт его адиабатич. сжатия кулоновскими силами, не допускающими различия в степени сжатия ионов и электронов (к-рое привело бы к сильному пространственному разделению зарядов). Релаксация в У. в. связана с обменом энергией при столкновениях электронов с ионами, приводящим к выравниванию темп-р электронного и ионного газов. Релаксация происходит очень медленно (по сравнению с процессами в СУ), т. к. доля передаваемой энергии при одном столкновении частиц, сильно различающихся по массе, очень мала. В формировании структуры У. в. важную роль играет электронная теплопроводность, к-рая гораздо больше ионной и приводит к заметному прогреву электронного газа перед СУ (рис. 7)
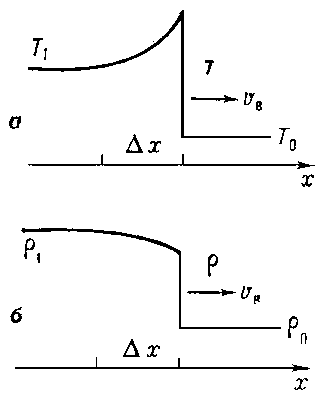
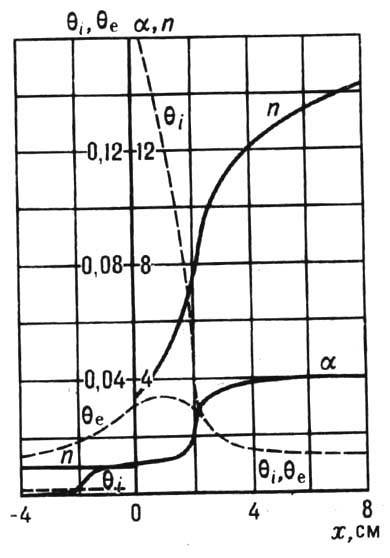
Рис. 7. Распределения ионной Т i (сплошная линия) и электронной Т е (штриховая линия) температур и плотности газа r во фронте ударной волны, распространя ющейся по плазме.
В У. в. с темп-рами в десятки и сотни тысяч К происходит многократная ионизация атомов. Достаточное нач. накопление электронов, за к-рым следует лавинообразная ионизация, обеспечивается фотоионизацией газа перед СУ УФ-излучением, приходящим из-за У. в. Вследствие сильного теплопроводного прогрева электронного газа уже перед СУ достигается значит. степень ионизации и от горячего электронного газа несколько нагревается и ионный. На рис. 8 показаны результаты расчёта структуры, подобной У. в., распространяющейся в сильно разреженной атмосфере, когда лучистый теплообмен (см. ниже) не играет роли. Плотн. r 1 соответствует высоте
70 км над уровнем моря.
Измерение яркости У. в. позволяет судить о темп-ре T 2 . При T 2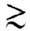 
10000 К прогретый слой воздуха частично экранирует видимое излучение газа, идущее из-за У. в., к-рое в холодном воздухе распространялось бы практически без поглощения. Эффект экранировки не позволяет регистрировать очень высокие значения T 2 . В воздухе нормальной плотности яркостная темп-pa никогда не превышает 50000 К, сколь бы велика не была темп-pa T 2 .
Экспериментальные (в осн. в опытах с ударными трубами) и теоретич. исследования излучения У. в. имеют большое практич. значение в связи с проблемами защиты сверхзвуковых летательных аппаратов от радиац. перегрева, создания мощных импульсных источников эл.-магн. излучения и др.
Магнитогидродинамические У. в. распространяются в электропроводящем (ионизованном) газе в присутствии внеш. магн. поля. Их теория строится на основе ур-ний магнитной гидродинамики. Соотношения типа (1) с учётом магн. сил дополняются условиями, к-рым подчиняются электрич. и магн. поля на границе двух сред. Магн. эффекты проявляются тем сильнее, чем больше отношение магн. давления H 2 /8pк давлению газа, где H- напряжённость магн. поля. Благодаря дополнит. параметрам и переменным, характеризующим величину и направление магн. поля по обе стороны разрыва, магнитогидродинамич. У. в. отличаются большим разнообразием свойств по сравнению с обычными У. в.
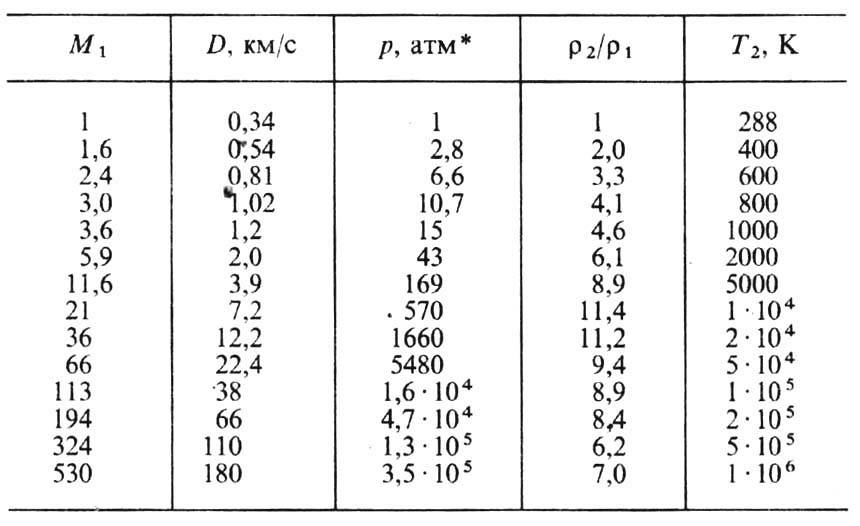
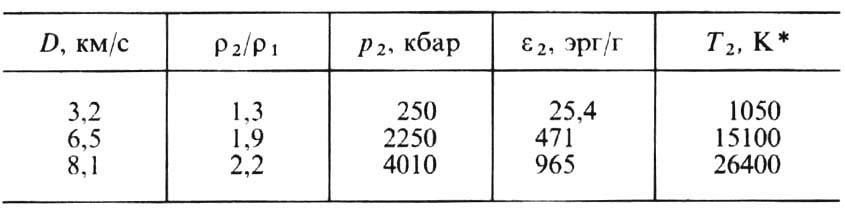
к-рые следуют из (2), и найти затем e 2 из (3). (Скорость и измеряется эл.-магн. методом или т. н. методом откола- путём измерения скорости откалывающейся пластины, образующейся при выходе У. в. на свободную поверхность исследуемого образца.) Произведя измерения и расчёты при разл. интенсивностях У. в., находят зависимость р 2 и e 2 от u 2 на УA. Иногда вместо или дополнительно к скорости и измеряют давление (пьезодатчиком), плотность (рентген) или темп-ру (в прозрачных веществах). (Применительно к конденсир. средам такие измерения менее универсальны и обычно технически более сложны.) В табл. 2 приведены данные для УA свинца:
, 
.
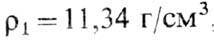
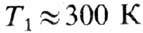
* Значения T 2 вычислены по ур-нию состояния.
УАжидкостей и (с точностью до сравнительно малых отклонений, связанных с изменением характера деформации при переходе через предел упругости) твёрдых тел при малых степенях сжатия,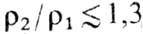 
, мало отличаются от изоэнтропы и обычно хорошо аппроксимируются ф-лой
400-450 кбар, тогда как в термодинамич. равновесных условиях образование стишовита в У. в. начиналось и заканчивалось бы в относительно узком интервале давлений в окрестности точки с давлением
100 кбар. Не претерпевший фазового превращения кварцит теряет устойчивость и аморфизуется при давлениях 230-300 кбар.
У. в. используются в наукоёмких технол. процессах упрочнения машиностроительных деталей, резки и сварки металлов, прессования порошков и др.
Лит.:1)Ландау Л. Д., Лифшиц E. M., Гидродинамика, 4 изд., M., 1988; 2) Зельдович Я. Б., Райзер Ю. П., Физика ударных волн и высокотемпературных гидродинамических явлений, 2 изд., M., 1966; 3) Кузнецов H. M., Термодинамические функции и ударные адиабаты воздуха при высоких температурах, M., 1965; 4) Ступоченко E. В., Лосев С. А., Осипов А. И., Релаксационные процессы в ударных волнах, M., 1965; 5) Be-ликовичА. Л., Либерман M. А., Физика ударных волн в газах и плазме, M., 1987; 6) Арцимович Л. А., Сагдеев P. 3., Физика плазмы для физиков, M,, 1979; 7) Ландау Л. Д., Лифшиц E. M., Электродинамика сплошных сред, 2 изд., M., 1982; 8) Кузнецов H. M., Устойчивость ударных волн, «УФН», 1989, т. 159, в. 3, с. 493; 9) Альтшулер Л. В., Применение ударных волн в физике высоких давлений, «УФН», 1965, т. 85, в. 2, с. 197; 10) Динамические исследования твердых тел при высоких давлениях, Сб., пер. сангл., M., 1965; 11) Аврорин E. H. [и др.], Мощные ударные волны и экстремальные состояния вещества, «УФН», 1993, т. 163, № 5, с. 1.
H. M. Кузнецов, Ю. П. Райзер.