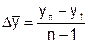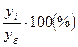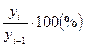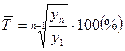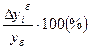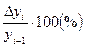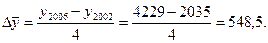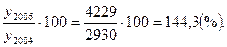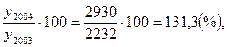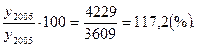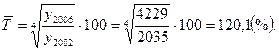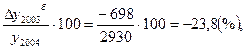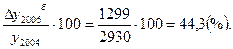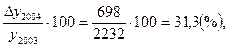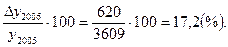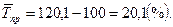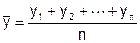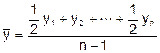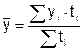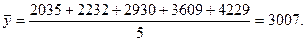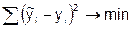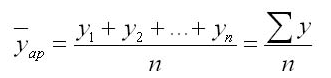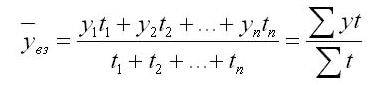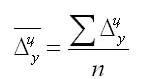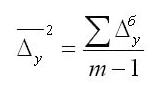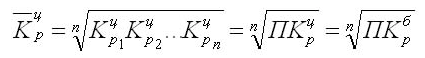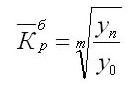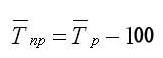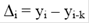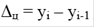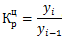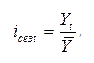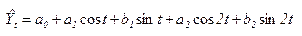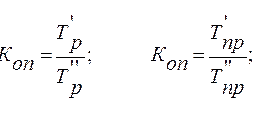Что называется тенденцией динамического ряда
Ряды динамики



Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, т. е. их динамика. Эта задача решается при помощи анализа рядов динамики (временных рядов).
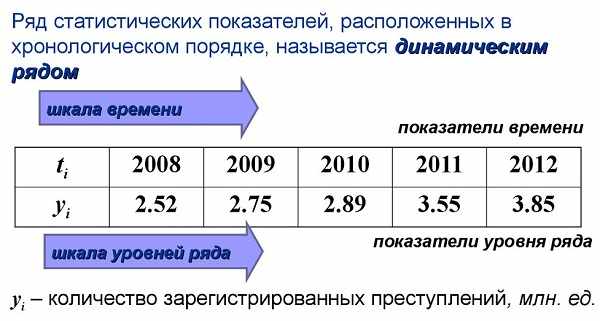
Ряд динамики (временной ряд) представляет собой ряд, рacположенных в хронологической последовательности числовых значений статистического показателя, характеризующего изменение изучаемого явления во времени.
В каждом ряду динамики имеются два основных элемента:
1) показатель времени t;
Показателями времени могут быть периоды (год, квартал, месяц, сутки) и моменты (определенная дата на начало или конец периода).
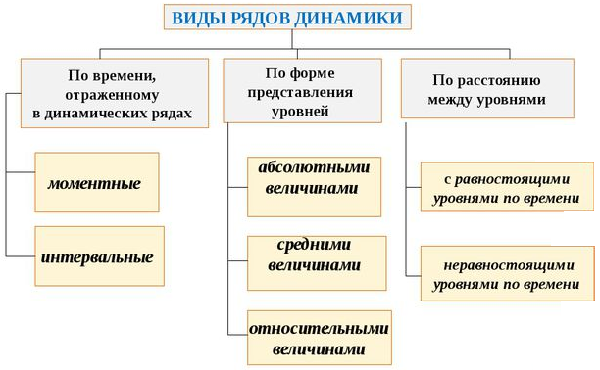
По времени ряды разделяются на моментные и интервальные.
Моментным называется ряд динамики, уровни которого характеризуют состояние явления на определенные даты(моменты времени). Например, число нерассмотренных дел в суде, находящихся в остатке на конец отчетного периода – на 1 июля 2010 г., число приостановленных дел на данную дату, число лиц, находящихся в розыске на отчетную дату).
Интервальным (периодическим) рядом динамики называется такой ряд, уровни которого характеризуют размер явления за конкретный период времени (год, квартал, месяц). Например, число рассмотренных гражданских дел с вынесением решения за 2009 год мировыми судьями или число лиц, в отношении которых были вынесены оправдательные приговоры по первой инстанции в 1 полугодии 2010 г.
Для количественной оценки динамики правовых явлений применяются такие статистические показатели как абсолютные приросты, темпы роста, темпы прироста, которые делятся на базисные, цепные и средние. В основе расчета этих показателей динамики лежит сравнение уровней ряда динамики. Если сравнение осуществляется с одним и тем же уровнем, принятым за базу сравнения, то эти показатели называются базисными. В качестве базисного выбирается либо начальный уровень в ряду динамики, либо уровень с которого начинается какой-то новый этап развития явления (например, число осужденных по статьям УК РФ с 1997 года – года вступления в силу нового Уголовного кодекса). Если сравнение осуществляется при переменной базе и каждый последующий уровень ряда сравнивается с предыдущим, то вычисленные таким образом показатели динамики называются цепными.
Для рядов динамики со значительными колебаниями уровней в качестве базы сравнения применяются средние уровни.
Абсолютный прирост (Δу) равен разности двух сравниваемых уровней.
Базисный абсолютный прирост
Цепной абсолютный прирост
Средний абсолютный прирост
Базисный темп роста Ti б =
Цепной темп роста Ti=
Средний темп роста
Замечание. Если темп роста и средний темп роста вычисляются в долях (не умножаются на 100%), то они называются соответственно коэффициентом роста и средним коэффициентом роста.
Темп прироста вычисляется как отношение абсолютного прироста (Δу) к уровню, принятому за базу сравнения. Темп прироста показывает, на сколько процентов изменился сравниваемый уровень по отношению к уровню, принятому за базу сравнения. Он может быть положительным, отрицательным или равным нулю.
Базисный темп прироста Тпр i б =
Цепной темп прироста Тпр i=
Средний темп прироста 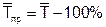
Замечание. Если вычислен соответствующий темп роста, то темп прироста равен:
Пример. Рассчитать абсолютные приросты, темпы роста и темпы прироста числа осужденных за взяточничество базисным и цепным способом, используя данные таблицы 8. За базу взять 2004 год.
Используя приведенные выше формулы, получим:
Базисный абсолютный прирост
Цепной абсолютный прирост
Средний абсолютный прирост
Базисный темп роста
T б 2002= 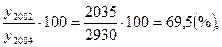
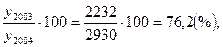
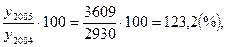
T2003= 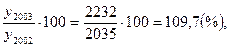
T2005= 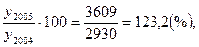
Средний темп роста
Базисный темп прироста
Тпр б 2002= 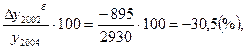
Тпр б 2005= 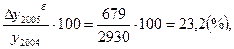
Цепной темп прироста
Тпр2003= 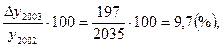
Тпр 2005= 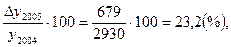
Средний темп прироста
Наряду с указанными показателями в ряду динамики может быть рассчитан средний уровень ряда. Он применим для любого ряда динамики: интервального и моментного.
В интервальных рядах динамики средний уровень (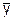
В моментном ряду с неравными интервалами времени средний уровень ряда определяется по формуле средней арифметической взвешенной
Пример. Рассчитатьсредний уровень ряда числа осужденных за взяточничество, используя данные таблицы 8.
Используя приведенную выше формулу для интервального ряда динамики, получим:
На практике принято считать, что значения уровней рядов динамики статистических показателей формируются под воздействием следующих компонент: тренда, сезонной, циклической и случайной составляющих. В большинстве случаев фактический уровень ряда динамики можно представить как сумму или произведение указанных выше компонентов. Модель, в которой ряд динамики представлен как сумма перечисленных компонент, называется аддитивной моделью ряда динамики. Модель, в которой ряд динамики представлен как произведение перечисленных компонент, называется мультипликативной моделью ряда динамики. Основная задача исследования отдельного ряда динамики – выявление и придание количественного выражения каждой из перечисленных выше компонент с тем, чтобы использовать полученную информацию для прогнозирования будущих значений ряда.
Подтрендомпонимают плавноеизменение, определяющее общее направлениеразвития, основную тенденцию ряда динамики. Это систематическая составляющая, характеризующая долговременное воздействие факторов на динамику изучаемого показателя.
Если период колебаний не превышает одного года, то их называют сезонными. Чаще всего причиной их возникновения считаются природно-климатические условия, обуславливающие социально-экономические явления (в сезон отпусков увеличивается количество квартирных краж, уменьшается число подаваемых в суды исков от физических лиц и т.п.).
При большем периоде колебания, считают, что в рядах динамики имеет место циклическая составляющая. Примерами могут служить демографические, инвестиционные и другие циклы.
Если из временного ряда удалить тренд и периодические составляющие, то останется случайная компонента, являющаяся результатом действия большого числа побочных факторов. Влияние каждого из таких факторов незначительно, но ощущается их суммарное воздействие. В судебной статистике одним из таких случайных факторов, который может оказывать существенное влияние на динамику, является изменение законодательства.
Важной задачей, решаемой с использованием рядов динамики, является определение общей тенденции развития, т.е. тренда. Выявление тренда в статистике называют также выравниванием ряда динамики, а методы выявления основной тенденции – методами выравнивания.
Выравнивание можно осуществлять разными способами: методом укрупнения интервалов, сглаживанием методом скользящей средней или аналитическим выравниванием.
Метод укрупнения интервалов заключается в преобразовании первоначального ряда динамики в ряд более продолжительных периодов (месячные в квартальные, квартальные в годовые и т. д.).
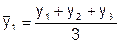
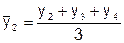
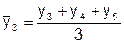
Первые два метода дают возможность определить лишь общую тенденцию развития явления, но получить обобщенную статистическую модель тренда посредством этих методов нельзя. Для того чтобы дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во времени используется аналитическое выравнивание ряда динамики.
Основными моделями общей тенденции рядов динамики являются следующие:
1. Равномерное развитие отображается уравнением прямолинейной функции 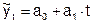
Параметр а1 определяет направление развития. Если а1 > О, то уровни ряда динамики равномерно возрастают, если а1
Ряды динамики
Понятие рядов динамики (временных рядов)
Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, то есть их динамика. Эта задача решается при помощи анализа рядов динамики (временных рядов).
Ряд динамики (или временной ряд) – это числовые значения определенного статистического показателя в последовательные моменты или периоды времени (т.е. расположенные в хронологическом порядке).
Числовые значения того или иного статистического показателя, составляющего ряд динамики, называют уровнями ряда и обычно обозначают буквой y. Первый член ряда y1 называют начальным или базисным уровнем, а последний yn – конечным. Моменты или периоды времени, к которым относятся уровни, обозначают через t.
Ряды динамики, как правило, представляют в виде таблицы или графика, причем по оси абсцисс строится шкала времени t, а по оси ординат – шкала уровней ряда y.
Пример ряда динамики
Таблица. Число жителей России в 2004-2009 гг. в млн.чел, на 1 января
| Год | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 |
| Число жителей | 144,2 | 143,5 | 142,8 | 142,2 | 142,0 | 141,9 |
График ряда динамики числа жителей России в 2004-2009 гг. в млн.чел, на 1 января
Данные таблицы и графика наглядно иллюстрируют ежегодное снижение числа жителей России в 2004-2009 годах.
Виды рядов динамики
Ряды динамики классифицируются по следующим основным признакам:
В нашем примере про число жителей России ряд динамики: 1) моментный (приведены уровни на 1 января); 2) абсолютных величин (в млн.чел.); 3) равномерный (равные интервалы в 1 год); 4) изолированный.
Показатели изменения уровней ряда динамики
Анализ рядов динамики начинается с определения того, как именно изменяются уровни ряда (увеличиваются, уменьшаются или остаются неизменными) в абсолютном и относительном выражении. Чтобы проследить за направлением и размером изменений уровней во времени, для рядов динамики рассчитывают показатели изменения уровней ряда динамики:
Все эти показатели могут определяться базисным способом, когда уровень данного периода сравнивается с первым (базисным) периодом, либо цепным способом – когда сравниваются два уровня соседних периодов.
Базисное абсолютное изменение представляет собой разность конкретного и первого уровней ряда, определяется по формуле
Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-того) периода больше или меньше первого (базисного) уровня, и, следовательно, может иметь знак «+» (при увеличении уровней) или «–» (при уменьшении уровней).
Цепное абсолютное изменение представляет собой разность конкретного и предыдущего уровней ряда, определяется по формуле
Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-того) периода больше или меньше предыдущего уровня, и может иметь знак «+» или «–».
В следующей расчетной таблице в столбце 3 рассчитаны базисные абсолютные изменения, а в столбце 4 – цепные абсолютные изменения.
| Год | y |  |  |  |  |  , % , % |  ,% ,% |
| 2004 | 144,2 | ||||||
| 2005 | 143,5 | -0,7 | -0,7 | 0,995 | 0,995 | -0,49 | -0,49 |
| 2006 | 142,8 | -1,4 | -0,7 | 0,990 | 0,995 | -0,97 | -0,49 |
| 2007 | 142,2 | -2,0 | -0,6 | 0,986 | 0,996 | -1,39 | -0,42 |
| 2008 | 142,0 | -2,2 | -0,2 | 0,985 | 0,999 | -1,53 | -0,14 |
| 2009 | 141,9 | -2,3 | -0,1 | 0,984 | 0,999 | -1,60 | -0,07 |
| Итого | -2,3 | 0,984 | -1,60 |
Между базисными и цепными абсолютными изменениями существует взаимосвязь: сумма цепных абсолютных изменений равна последнему базисному изменению, то есть

Базисное относительное изменение (базисный темп роста или базисный индекс динамики) представляет собой соотношение конкретного и первого уровней ряда, определяясь по формуле
Цепное относительное изменение (цепной темп роста или цепной индекс динамики) представляет собой соотношение конкретного и предыдущего уровней ряда, определяясь по формуле

Относительное изменение показывает во сколько раз уровень данного периода больше уровня какого-либо предшествующего периода (при i>1) или какую его часть составляет (при i Следующая лекция.
Ряды динамики в статистике
Статистика занимается не только обработкой накопленных данных, но и нахождением тенденций в различных парных показателях, которые связаны друг с другом, что успешно решается применением инструмента «ряды динамики в статистике».
Классическим примером является изменение каких-либо показателей за определенный промежуток времени, что в конце концов сводится не к изучению попарной зависимости (показатель время), а к изучению изменений показателей в динамике.
Понятие о рядах динамики
Строгое понятие для ряда динамики обозначено в статистике так.
Динамические ряды (иными словами ряд динамики или временной ряд) – это распределенные в увеличивающемся порядке дискретных значений выбранного статистического параметра за последовательные временные промежутки.
Если рассмотреть динамический ряд, будет очевидно, что он наполнен данными в формате y1t1, y2t2, y3t3…yntn. Применительно к временному ряду, значением у будет называться «уровень ряда», при этом первый член ряда (у1) называется базисным (начальным) уровнем, а уn – конечным уровнем. Через обозначение t будет обозначаться временной показатель, который соответствует каждому из уровней ряда.
При построении графической зависимости временного ряда, функция будет иметь вид t(y), где по оси y (ординат) будут отложены значения уровней ряда (параметр у), а по оси х (ось абсцисс) будут отложены временные значения параметра t.
Пример ряда динамики и его характеристика
В качестве примера, рассмотрим следующий ряд.
Таблицу можно озаглавить так: «Годовой выпуск препарата «Ибупрофен» в 2013-2018гг. в млн. уп.»
| Год | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
| Годовой объем выпуска, млн. уп. | 88,1 | 91,3 | 96,5 | 99,3 | 101,8 | 100,7 |
В данном ряду можно обнаружить присутствие следующих показателей:
На основании изложенного, можно сделать вывод, что перед нами находится временной ряд.
Виды рядов динамики
В зависимости от характеризующего критерия, существует несколько разновидностей динамических рядов.
По временной характеристике различают моментальные и интервальные:
При характеристике по показателю t выделяют неполные и полные ряды. Неполными считаются такие, в которых не соблюдается одинаковый промежуток между соседними значениями времени. Для полных, такой интервал соблюден.
Кроме этого, существует классификация по количеству показателей. Существуют изолированные – во времени анализируется всего один показатель и многомерные, когда во времени анализ ведется для целого ряда параметров, которые связаны между собой одним процессом.
Правила построения рядов динамики
Когда производится построение временных рядов, то для них должны соблюдаться общие требования:
Средние характеристики ряда динамики
Главный показатель, характеризующий среднее значение абсолютных показателей (y1, y2…yn) – это средний уровень ряда. Если основные интервалы не изменялись, то следует пользоваться выражением для расчета (где t – количество уровней):
Чуть сложнее будет выглядеть методика расчета, если были временные пропуски или они неравны. Вычисления выполняются через арифметическую взвешенную:
Здесь y1, y2…yn – это абсолютные уровни ряда, а t1, t2…tn – протяженности временных интервалов.
Для описания удобно пользоваться параметром среднего абсолютного прироста, представляющим собой среднее от прироста за равные временные промежутки. Когда использованы гармоничные интервалы, формула выглядит так:
Для приведенного выражения обозначение n – это число приростов за выбранный период.
Также есть методика расчетов с использованием базисного абсолютного прироста при равенстве интервалов для смыкания рядов:
Значение m – это количество уровней в выбранном периоде.
Показательная характеристика средний темп роста, он отображает как происходило изменение уровней рядя (коррелируя с единицами времени). Вычисления для цепных показателей выведены через расчет средней геометрической:
В данном выражении n количество цепных коэффициентов, Кц – сами цепные коэффициенты.
Когда даны все значения уровней, то выражение значительно упрощается:
Иногда требуется охарактеризовать срединный темп прироста, рассчитывающийся по уравнению на основании уже известных средних темпов роста (Тр):
Показатели анализа рядов динамики
Всего имеются 5 характеристик, предназначающихся для выполнения анализа:
Анализ сезонных колебаний
Если взять для анализа временной ряд, в котором собраны объемы продаж противовирусных препаратов за 5 лет, то будет очевидно, что ежегодно происходят колебания (снижение или увеличение) продаж, которые повторяются. Такие колебания будут именоваться сезонными.
Чтобы устранить нежелательное влияние таких колебаний, проводится аналитическое изучение, выполняющееся либо с помощью гармонического исследования, либо с учетом индекса сезонности.
Индекс сезонности это фактическая характеристика того, в какое количество раз анализируемый уровень увеличен или уменьшен относительно срединного:
Тут Yt – это уровень, предполагаемый к анализу, а Ȳ это средний уровень всего ряда.
Более сложный анализ предполагает выделение гармонических колебаний. Для этого производится выравнивание по ряду Фурье (так называемые «гармоники»), и высчитывают, какие гармоники наиболее сопоставимы с анализируемым рядом. Общий вид ряда Фурье для двух гармоник выражается формулой:
Индекс сезонности
Для того чтобы не вычислять относительную разницу в процентах между каждым месяцем во временном ряду, можно вычислить один параметр – индекс сезонности.
Индекс сезонности рассчитывается на основании следующих показателей:
По результатам сопоставления получается значение, которое так или иначе соотносится с уровнем в 100%. Если присутствует значимое отклонение в меньшую сторону, то это является свидетельством присутствия сезонного колебания.
Приведение рядов динамики к одинаковому основанию
Во время работы с несколькими явлениями, описывающими один процесс, может вызывать интерес сопоставление рядов динамики. С целью корректного сопоставления потребуется приведение к одному основанию. Сопутствующей операцией является вычисление коэффициента опережения или отставания.
К каждому ряду находится базисный уровень и вычисляются темпы роста и прироста рядов. Для каждого ряда должен быть выбран аналогичный временной интервал.
Сравнение проводится на основании отношения базисного темпа роста (опционально – прироста) в аналогичном временной интервале. Выражения для расчета достаточно просты:
Аналитическое выравнивание ряда динамики
При определении каких-либо закономерностей во временных рядах и возможности прогнозирования отдельных тенденций, применяется методика аналитического выравнивания. С этой целью производится приближение к определенной алгебраической зависимости, наиболее точно описывающей ряд.
Методика укрупнения интервалов представляет собой преобразование, когда временные промежутки делаются более длительными, что позволяет более точно оценить общий вектор тенденции и понять, какое направление будет иметь зависимость.
Методика скользящей средней основана на особенности временных рядов погашать случайные отклонения от среднего уровня. Каждому звену с использованием простого среднеарифметичнского значения нужно рассчитывать уровень, в котором рандомные колебания сведены к минимуму.
Методика аналитического выравнивания под конкретный ряд подбирается зависимость, которая более полно отражает алгебраическую зависимость.
Примеры решения задач на тему «Ряды динамики в статистике»
Классическим упражнением является определение вида и показателей для ряда динамики.
Задача. Для указанного временного ряда высчитать: его вид, цепной и базисный прирост, темп роста/прироста, средний темп прироста.
| Отчетный год | Суммарный объем производства, млрд. руб. |
| 2014 | 18 |
| 2015 | 16 |
| 2016 | 17 |
| 2017 | 16 |
| 2018 | 12 |
Согласно определению, этот ряд динамики относится к интервальному, поскольку в условии приведен четкий промежуток времени. Произведем расчет показателей.
Абсолютные приросты (по цепному способу):
16 – 18 = 2 млрд. руб.
17 – 16 = 1 млрд. руб.
16 – 17 = 1 млрд. руб.
12 – 16 = 4 млрд. руб.
Абсолютные приросты (по базисному методу):
17 – 18 = 1 млрд. руб.
12 – 18 = 6 млрд. руб.
Цепные темпы роста:
Базисные темпы роста:
Цепные темпы прироста:
Базисные темпы прироста:
Средний уровень временного ряда:
(18 + 16 + 17 + 16 + 12) / 5 = 15,8.
Среднегодовой абсолютный прирост:
Среднегодовой темп прироста:
Таким образом временные ряды занимают важное место среди статистических объектов.
Основное их преимущество заключается в широком практическом применении, которое позволяет использовать ряды динамики для наблюдений за физическими величинами и экономическими показателями. Важно знать о нюансах, которые помогут правильно проанализировать такие ряды.