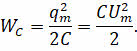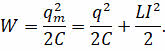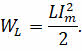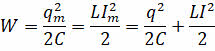Что называется свободными электромагнитными колебаниями

Физика. 11 класс

Конспект урока

Урок 7. Свободные и вынужденные электромагнитные колебания. Колебательный контур

Перечень вопросов, рассматриваемых на уроке:

1) электромагнитные колебания, колебательный контур;

2) универсальность основных закономерностей колебательных процессов для колебаний любой физической природы;

3) гармонические колебания;

4) физический смысл характеристик колебаний.

5) графики зависимости электрического заряда, силы тока и напряжения от времени при свободных электромагнитных колебаниях.

6) определение по графику характеристик колебаний;

7) аналогия между механическими и электромагнитными колебаниями.

Электромагнитными колебаниями называют периодические изменения со временем заряда, силы тока и напряжения.

Свободными колебаниями называют колебания, возникающие в колебательной системе за счет первоначально сообщенной этой системе энергии.

Система, состоящая из конденсатора и катушки индуктивности, присоединенной к его обкладкам, называется колебательным контуром.

Период электромагнитных колебаний – промежуток времени, в течение которого ток в колебательном контуре и напряжение на пластинах конденсатора совершает одно полное колебание.

Частота колебаний – число колебаний в единицу времени.

Основная и дополнительная литература по теме урока:

Основное содержание урока

Колебательным контуром называется система, состоящая из конденсатора и катушки, присоединенной к его обкладкам, в которой могут происходить свободные электромагнитные колебания

Электромагнитные колебания в контуре происходят с большой частотой и определять его характеристики без осциллографа невозможно.

Развертка получаемая на экране осциллографа схожа с той, что вычерчивает маятник с песочницей над движущимся листом бумаги при колебаниях математического маятника.

Чтобы в колебательном контуре возникли колебания, необходимо сообщить колебательному контуру энергию, зарядив конденсатор от источника тока.

Энергия, полученная конденсатором заключена в электрическом поле обкладок

где — заряд конденсатора, C – его электроемкость.

Между обкладками конденсатора возникает разность потенциалов .

При разрядке конденсатора энергия электрического поля превращается в энергию магнитного поля, определяемая по формуле

где – индуктивность катушки, – сила переменного тока.

Полная энергия колебательного контура равна

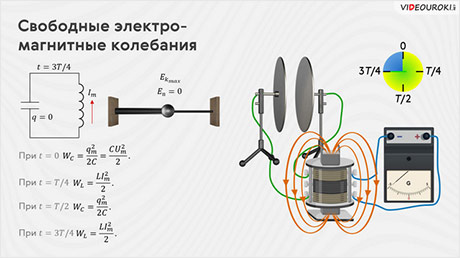
Когда конденсатор разрядится полностью, вся энергия электрического поля превращается в энергию магнитного поля. Когда сила тока и созданное им магнитное поле начинает уменьшаться, возникает ЭДС самоиндукции, стремящийся поддержать ток, и начинается перезарядка конденсатора. При свободных колебаниях через промежутки времени, равные периоду колебаний, состояние системы в точности повторяется. Полная энергия такой системы любой момент времени равно максимальной энергии электрического поля или максимальной энергии магнитного поля.

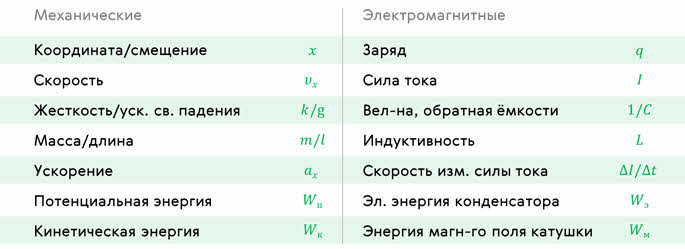
Электромагнитные колебания в контуре имеют сходство со свободными механическими колебаниями. Характер периодического изменения различных величин одинаков. При механических колебаниях периодически изменяются координата тела x и проекция его скорости , а при электромагнитных колебаниях изменяются заряд q конденсатора и сила тока i в цепи.

Индуктивность катушки L аналогична массе тела m, при колебаниях груза на пружине, кинетическая энергия тела , аналогична энергии магнитного поля тока .

Роль потенциальной энергии выполняет энергия заряда конденсатора:

Координата тела аналогична заряду конденсатора.

Полная энергия колебательного контура, в любой момент времени, равна сумме энергий магнитного и электрического полей:

Производная полной энергии по времени равна нулю при R = 0. Следовательно, равна нулю сумма производных по времени от энергий магнитного и электрического полей:

Электрический заряд и сила тока, при свободных колебаниях с течением времени изменяются по закону синуса или косинуса, то есть совершают гармонические колебания.

Циклическая частота для свободных электрических колебаний:

Период свободных колебаний в контуре равен:

Период свободных электрических колебаний в колебательном контуре зависит от индуктивности катушки и емкости конденсатора.

Период электромагнитных колебаний – промежуток времени, в течение которого ток в колебательном контуре и напряжение на пластинах конденсатора совершает одно полное колебание.

Частотой колебаний называется величина, обратная периоду колебаний:

Частоту свободных колебаний называют собственной частотой колебательной системы.

Заряд конденсатора изменяется по гармоническому закону:

где – амплитуда колебаний заряда. Сила тока также совершает гармонические колебания:

где – амплитуда колебаний силы тока. Колебания силы тока опережают по фазе колебания заряда на .

Разбор типовых тренировочных заданий

Задача 1. Идеальный колебательный контур состоит из конденсатора ёмкостью 2 мкФ и катушки индуктивности. В контуре происходят свободные электромагнитные колебания. В таблице приведена зависимость энергии W, запасённой в конденсаторе идеального колебательного контура, от времени t.

Источник

Электромагнитные колебания

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: свободные электромагнитные колебания, колебательный контур, вынужденные электромагнитные колебания, резонанс, гармонические электромагнитные колебания.

Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.

Колебательный контур

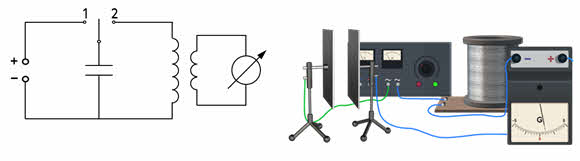
Колебательный контур — это замкнутый контур, образованный последовательно соединёнными конденсатором и катушкой.

Зарядим конденсатор, подключим к нему катушку и замкнём цепь. Начнут происходить свободные электромагнитные колебания — периодические изменения заряда на конденсаторе и тока в катушке. Свободными, напомним, эти колебания называются потому, что они совершаются без какого-либо внешнего воздействия — только за счёт энергии, запасённой в контуре.

Рассмотрим подробно все важные стадии процесса колебаний. Для большей наглядности будем проводить аналогию с колебаниями горизонтального пружинного маятника.

Несмотря на то, что сопротивление катушки равно нулю, ток не возрастёт мгновенно. Как только ток начнёт увеличиваться, в катушке возникнет ЭДС самоиндукции, препятствующая возрастанию тока.

Аналогия. Маятник оттянут вправо на величину и в начальный момент отпущен. Начальная скорость маятника равна нулю.

Увеличение тока происходит постепенно: вихревое электрическое поле катушки препятствует нарастанию тока и направлено против тока.

Напряжение на катушке равно нулю, но ток не исчезнет мгновенно. Как только ток начнёт уменьшаться, в катушке возникнет ЭДС самоиндукции, препятствующая убыванию тока.

Сила тока убывает постепенно: вихревое электрическое поле катушки, поддерживая убывающий ток, сонаправлено с током.

Аналогия. Маятник продолжает двигаться влево — от положения равновесия к правой крайней точке. Скорость его постепенно убывает, деформация пружины увеличивается.

Аналогия. Маятник двигается обратно: от правой крайней точки к положению равновесия.

Аналогия. Маятник продолжает двигаться вправо — от положения равновесия к крайней левой точке.

Аналогия. Маятник вернулся в исходное положение.

Рассмотренные электромагнитные колебания являются незатухающими — они будут продолжаться бесконечно долго. Ведь мы предположили, что сопротивление катушки равно нулю!

Точно так же будут незатухающими колебания пружинного маятника при отсутствии трения.

В реальности катушка обладает некоторым сопротивлением. Поэтому колебания в реальном колебательном контуре будут затухающими. Так, спустя одно полное колебание заряд на конденсаторе окажется меньше исходного значения. Со временем колебания и вовсе исчезнут: вся энергия, запасённая изначально в контуре, выделится в виде тепла на сопротивлении катушки и соединительных проводов.

Точно так же будут затухающими колебания реального пружинного маятника: вся энергия маятника постепенно превратится в тепло из-за неизбежного наличия трения.

Энергетические превращения в колебательном контуре

Поскольку тепловых потерь нет, энергия из контура не уходит: она постоянно перераспределяется между конденсатором и катушкой.

Соотношение (1) применяется при решении многих задач.

Электромеханические аналогии

В предыдущем листке про самоиндукцию мы отметили аналогию между индуктивностью и массой. Теперь мы можем установить ещё несколько соответствий между электродинамическими и механическими величинами.

Для пружинного маятника мы имеем соотношение, аналогичное (1) :

Здесь, как вы уже поняли, — жёсткость пружины, — масса маятника, и — текущие значения координаты и скорости маятника, и — их наибольшие значения.

Опираясь на эти электромеханические аналогии, мы можем предвидеть формулу для периода электромагнитных колебаний в колебательном контуре.

В самом деле, период колебаний пружинного маятника, как мы знаем, равен:

Электромеханические аналогии не подводят: формула (7) даёт верное выражение для периода колебаний в колебательном контуре. Она называется формулой Томсона. Мы вскоре приведём её более строгий вывод.

Гармонический закон колебаний в контуре

Напомним, что колебания называются гармоническими, если колеблющаяся величина меняется со временем по закону синуса или косинуса. Если вы успели забыть эти вещи, обязательно повторите листок «Механические колебания».

Колебания заряда на конденсаторе и силы тока в контуре оказываются гармоническими. Мы сейчас это докажем. Но прежде нам надо установить правила выбора знака для заряда конденсатора и для силы тока — ведь при колебаниях эти величины будут принимать как положительные, так и отрицательные значения.

Сначала мы выбираем положительное направление обхода контура. Выбор роли не играет; пусть это будет направление против часовой стрелки (рис. 10 ).

Рис. 10. Положительное направление обхода

Заряд конденсатора — это заряд той его пластины, на которую течёт положительный ток (т. е. той пластины, на которую указывает стрелка направления обхода). В данном случае — заряд левой пластины конденсатора.

Величины и меняются со временем, но энергия контура остаётся неизменной:

Но сила тока не является функцией, тождественно равной нулю; поэтому

Перепишем это в виде:

Эта величина называется ещё собственной частотой контура; именно с этой частотой в контуре совершаются свободные (или, как ещё говорят, собственные колебания). Период колебаний равен:

Мы снова пришли к формуле Томсона.

Гармоническая зависимость заряда от времени в общем случае имеет вид:

Циклическая частота находится по формуле (10) ; амплитуда и начальная фаза определяются из начальных условий.

Мы видим, что и сила тока меняется по гармоническому закону, на сей раз — по закону синуса:

Амплитуда силы тока равна:

Наличие «минуса» в законе изменения тока (13) понять не сложно. Возьмём, к примеру, интервал времени (рис. 2 ).

Рис. 11. Графики колебаний заряда и тока

Обратите внимание: нули заряда приходятся на максимумы или минимумы тока; и наоборот, нули тока соответствуют максимумам или минимумам заряда.

Используя формулу приведения

запишем закон изменения тока (13) в виде:

Опережение током заряда по фазе на графически проявляется в том, что график тока сдвинут влево на относительно графика заряда. Сила тока достигает, например, своего максимума на четверть периода раньше, чем достигает максимума заряд (а четверть периода как раз и соответствует разности фаз ).

Вынужденные электромагнитные колебания

Как вы помните, вынужденные колебания возникают в системе под действием периодической вынуждающей силы. Частота вынужденных колебаний совпадает с частотой вынуждающей силы.

Вынужденные электромагнитные колебания будут совершаться в контуре, поключённом к источнику синусоидального напряжения (рис. 12 ).

Рис. 12. Вынужденные колебания

Если напряжение источника меняется по закону:

Источник

Свободные электромагнитные колебания

Урок 10. Физика 11 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Свободные электромагнитные колебания»

Конденсатор — устройство, предназначенное для накопления электрического заряда и энергии электрического поля. Прообразом всех современных конденсаторов была лейденская банка, изобретённая в 1745 году Питером ван Мушенбруком.

После того как лейденской банке научились сообщать большой заряд с помощью электростатической машины, началось подробное изучение её электрического разряда. Так, замыкая обкладки лейденской банки на катушку со стальным сердечником, было обнаружено намагничивание последнего. С одной стороны, в этом нет ничего удивительного, ведь мы знаем, что электрический ток порождает магнитное поле, которое, собственно, и намагничивает сердечник. Интересно было другое. Невозможно было предсказать, какой конец сердечника катушки окажется северным полюсом, а какой — южным.

Далеко не сразу поняли, что при разрядке конденсатора через катушку в электрической цепи возникают колебания, названные позже электромагнитными. Поэтому за время разрядки конденсатора ток в цепи много раз меняет направление. В результате этого сердечник и намагничивался каждый раз по-разному.

В настоящее время под электромагнитными колебаниями понимают периодические изменения заряда, напряжения и силы тока в электрической цепи.

Система, в которой могут происходить свободные электромагнитные колебания, называется колебательным контуром.

Простейший колебательный контур представляет собой электрическую цепь из последовательно соединённых катушки индуктивности и конденсатора.

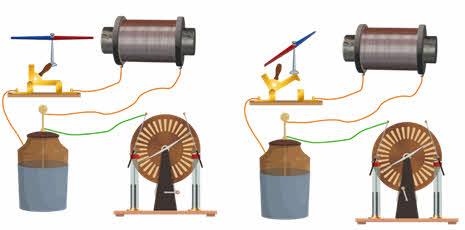
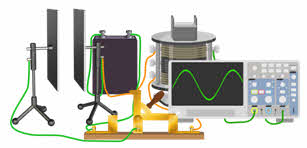
Давайте получим электромагнитные колебания. Для чего соберём цепь, состоящую из источника постоянного тока, катушки индуктивности с большим числом витков, на которую в средней её части, поверх первичной обмотки намотана вторичная обмотка с малым числом витков, и ключа. Вторичную обмотку катушки замкнём на гальванометр, с помощью которого будем регистрировать возникновение колебаний в контуре. Зарядим конденсатор, подключив его на некоторое время к источнику тока. А теперь перекинем ключ: стрелка гальванометра начала совершать колебания, фиксируя наличие переменного тока в катушке.

Если в такую цепь параллельно катушке включить электронный осциллограф, то на его экране мы получим временную развёртку колебаний, подобную той, что вычерчивает пружинный маятник на движущемся листе бумаги. Как видим, эти колебания затухают с течением времени. Поэтому они являются свободными.

Теперь давайте подробно рассмотрим процесс разрядки конденсатора и проследим за происходящими превращениями энергии. Итак, пусть в начальный момент времени наш конденсатор заряжен, а между его обкладками существует электрическое поле:

Эта ситуация эквивалентна ситуации с механическими колебаниями математического маятника и соответствует состоянию, когда его вывели из положения равновесия, тем самым сообщив потенциальную энергию.

При замыкании цепи, конденсатор начнёт разряжаться, под действием электрического поля заряды начнут двигаться по виткам катушки, создавая в цепи ток, сила которого постепенно увеличивается. В результате, как мы знаем, в катушке возникнет ток самоиндукции, противодействующий росту тока во внешней цепи. По мере разрядки конденсатора электрическое поле в нём будет ослабевать, а в катушке возникнет магнитное поле. При этом уменьшение энергии электростатического поля конденсатора равно увеличению энергии магнитного поля катушки:

В тот момент, когда конденсатор полностью разрядится, магнитное поле катушки будет самым сильным. Это означает, что энергия электрического поля конденсатора полностью перейдёт в энергию магнитного поля катушки:

Похожее происходит и с математическим маятником, при прохождении им положения равновесия, когда потенциальная энергия маятника полностью переходит в его кинетическую энергию.

Хотя в этот момент электрическое поле в конденсаторе отсутствует, заряды некоторое время будут двигаться в цепи в прежнем направлении по инерции. Сила тока в цепи начнёт постепенно уменьшаться, так как ток самоиндукции меняется на противоположный, поддерживающий убывающий ток в цепи.

В результате конденсатор снова зарядится, но заряды обкладок поменяются местами. Ток на мгновение прекратится и вся энергия магнитного поля катушки превратиться обратно в энергию электрического поля конденсатора.

Эта ситуация эквивалентна ситуации с механическими колебаниями, в момент отклонения маятника от положения равновесия в противоположную сторону, когда его кинетическая энергия полностью переходит в потенциальную.

Далее явление повторится в обратном порядке: конденсатор начнёт разряжаться и энергия его электрического поля будет преобразовываться в энергию магнитного поля катушки индуктивности. Но в этом случае через катушку течёт ток противоположного направления. Сила тока в катушке вновь достигнет своего максимального значения, когда конденсатор полностью разрядится. А значит, вся электрическая энергия превратится в энергию магнитного поля, аналогично тому, как маятник, возвращаясь, вновь проходит положение своего равновесия, и его потенциальная энергия полностью переходит в кинетическую.

После этого сила тока начинает уменьшаться, а конденсатор будет перезаряжаться. Когда ток в цепи прекратиться, конденсатор окажется заряженным так, как в начальный момент времени. Теперь опять вся энергия колебательного контура заключена в его электрическом поле, вторая перезарядка возвращает контур в исходное состояние. Эта ситуация аналогично тому, как маятник возвращается в своё исходное положение, а его кинетическая энергия полностью переходит в потенциальную.

Таким образом, завершилось полное колебание в контуре, и в дальнейшем процесс повторяется в уже рассмотренной нами последовательности. Минимальный промежуток времени, через который процесс в колебательном контуре полностью повторяется, называют периодом электромагнитных колебаний.

Как вы могли заметить, если в контуре отсутствует активное сопротивление, то его полная энергия сохраняется неизменной и её значение в любой момент времени равно либо максимальной энергии электрического поля, либо максимальной энергии поля магнитного:

Почему при рассмотрении процессов, происходящих в колебательном контуре, мы их сравнивали с колебаниями математического маятника? Дело в том, что эти процессы описываются одинаковыми уравнениями, что позволяет переносить закономерности, полученные при изучении одного вида колебаний, на колебания другой природы.

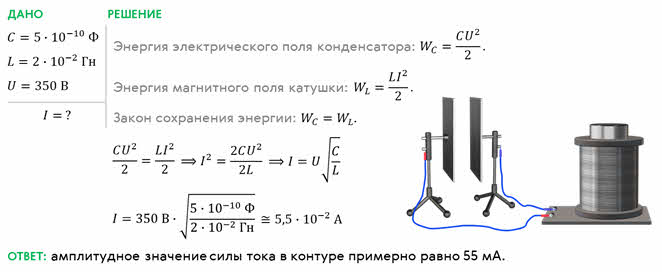
Для закрепления материала, решим с вами такую задачу: колебательный контур состоит из конденсатора ёмкостью 500 пФ и катушки, индуктивностью 20 мГн. Определите амплитудное значение силы тока в контуре, если амплитудное значение напряжения на конденсаторе составляет 350 В.

В заключение отметим ещё одну важную особенность электромагнитных колебаний: если не пополнять извне заряды на обкладках конденсатора, то колебания довольно быстро прекратятся, так как проводники обладают сопротивлением. При протекании в них тока, они нагреваются, на что расходуется энергия контура. Чтобы колебания не прекращались, необходимо к конденсатору подключить источник тока, напряжение которого изменяется периодически с определённой частотой, который и будет вбрасывать внутрь цепи новые порции энергии, не давая ей израсходоваться полностью. В этом случае в контуре будут существовать вынужденные электромагнитные колебания, происходящие с частотой, равной частоте изменения напряжения источника тока. Однако если частота переменного напряжения совпадёт с собственной частотой колебаний контура, то в цепи произойдёт резкое увеличение силы тока — возникнет резонанс. Это явление широко применяется в радиотехнике.

Источник