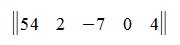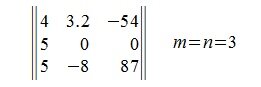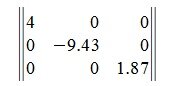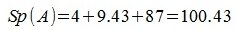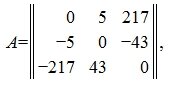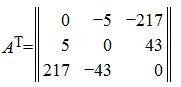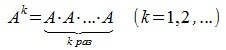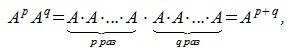Что называется суммой двух матриц
Операции над матрицами. Определение. Суммой двух матриц А и В одинаковой размерности m×n называется матрица С той же размерности
Определение. Суммой двух матриц А и В одинаковой размерности m×n называется матрица С той же размерности, элементы которой равны 
( 
; 
).
Для обозначения суммы двух матриц используется запись 
. Операция получения суммы матриц называется их сложением.
Теорема. Сложение матриц коммутативно, т. е.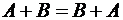 
.
Доказательство. Пользуясь определением суммы двух матриц и коммутативностью сложения чисел 
, убеждаемся в очевидности данного утверждения.■
Теорема. Сложение матриц ассоциативно, т. е.
.
Доказательство. Пользуясь определением суммы двух матриц и ассоциативностью сложения чисел, убеждаемся в очевидности данного утверждения.■
Эти теоремы позволяют не заботиться о порядке следования слагаемых матриц при сложении двух или большего числа матриц.
Определение. Произведением матрицы А (размерности m×n) на действительное число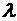 
называется матрица С той же размерности, элементы которой равны 
( ; ).
Для обозначения произведения матрицы на число используется запись 
или 
. Операция получения произведения матрицы на число называется умножением матрицы на это число.
Теорема. Умножение матрицы на число ассоциативно относительно числового множителя, т. е. 
.
Доказательство. Пользуясь определением произведения матрицы на число и ассоциативностью умножения чисел, убеждаемся в очевидности данного утверждения.■
Теорема. Умножение матрицы на число дистрибутивно относительно сложения матриц, т. е. 
.
Доказательство. Пользуясь определением произведения матрицы на число и дистрибутивностью умножения чиселотносительно их сложения, убеждаемся в очевидности данного утверждения.■
Теорема. Умножение матрицы на число дистрибутивно относительно сложения чисел, т. е. 
.
Доказательство. Пользуясь определением произведения матрицы на число и дистрибутивностью умножения чиселотносительно их сложения, убеждаемся в очевидности данного утверждения.■
Определение. Разностью двух матриц А и В одинаковой размерности m×n называется матрица С той же размерности, которая в сумме с матрицей В дает матрицу А.
Для обозначения разности двух матриц используется запись 
. Операция получения разности матриц называется их вычитанием. Легко убедиться, что разность С двух матриц А и В может быть получена по правилу 
.
Определение. Нулевой (не по внешнему виду, а по роли в алгебраической структуре) называется такая матрица О, что для любой матрицы А верно 
.
Легко убедиться, что единственной такой матрицей является матрица, которую мы раньше назвали нулевой по внешнему виду, т. е. матрица размерности той же, что и А, состоящая из одних нулей.
Определение. Противоположной к матрице А называется такая матрица (–А) той же размерности, что и А, для которой верно 
.
Легко убедиться, что (–А)= 
– единственная такая матрица для каждой матрицы А. Если А=О, то она противоположна сама себе.
Определение. Произведением матрицы А, имеющей размерность m×n, на матрицу В, имеющую размерность n×p, называется матрица С, имеющая размерность m×p, элементы которой равны 
( ; 
; 
).
Для обозначения произведения матрицы А на матрицу В используют запись 
. Операция получения произведения матрицы А на матрицу В называется перемножением этих матриц.
Матрицу А можно умножить не на всякую матрицу В: необходимо, чтобы число столбцов матрицы А было равно числу строк матрицы В. Оба произведения 
и 
можно определить лишь в том случае, когда число столбцов А совпадает с числом строк В, число строк А совпадает с числом столбцов В. При этом обе матрицы и будут квадратными, но размерности их будут, вообще говоря различными. Для того чтобы оба произведения и не только были определены, но и имели одинаковый порядок, необходимо и достаточно, чтобы обе матрицы А и В были квадратными матрицами одного и того же порядка.
Теорема. Умножение матриц (при условии, что оно определено) ассоциативно, т. е.
.
Доказательство.Чтобы произведения были возможны, необходимо, чтобы матрица А имела размерность m×n, матрица В имела размерность n×p, а матрица С имела размерность p×r. Тогда элемент 
матрицы 
равен 
, а элемент 
матрицы 
равен 
. Равенство 
вытекает из возможности изменения порядка суммирования относительно j и k.■
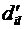
Теорема. Умножение матриц (при условии, что оно определено) дистрибутивно относительно сложения матриц, т. е. 
или 
.
Доказательство. Пользуясь определениями перемножения и сложения матриц и дистрибутивностью умножения чиселотносительно их сложения, убеждаемся в очевидности данного утверждения.■
Вопрос о коммутативности произведения матрицы А на матрицу В имеет смысл ставить лишь для квадратных матриц А и В одинаковой размерности, поскольку только для таких матриц А и В оба произведения АВ и ВА определены и являются матрицами одинаковых порядков.
Легко убедиться, что произведение двух квадратных матриц, вообще говоря, некоммутативно.
Действительно, пусть 
, 
. Тогда АВ= 
ВА= 
.
Определение. Единичной (не по внешнему виду, а по роли в алгебраической структуре) называется такая матрица Е, что для любой квадратной матрицы А верно 
или 
.
Легко убедиться, что единственной такой матрицей является матрица, которую мы раньше назвали единичной по внешнему виду, т. е. матрица размерности той же, что и А, у которой элементы главной диагонали равны единице, а все остальные – нулю. Действительно, если предположить, что 
– другая единичная матрица, то по определению 
. Причем 
, т. е. матрица Е является как левой единичная, так и правой единичной матрицей, поскольку коммутирует с любой квадратной матрицей.
Обратная матрица
Определение. Обратной к квадратной матрице А называется такая матрица 
той же размерности, что и А, для которой верно 
или 
.
Легко убедиться, что если для матрицы А существует правая обратная матрица В, т. е. 
, то она единственная, и существует левая обратная матрица С, которая совпадает с В, т. е. 
. Действительно, равенства 
показывают, что всякая левая обратная матрица С совпадает с В. Аналогично показывается, что всякая правая обратная матрица совпадает с С, а на основании выше доказанного, совпадает и с В.
Остался открытым вопрос существования обратной матрицы.
Определение.Невырожденной называется матрица, определитель которой отличен от нуля.
Теорема. Обратная матрица существует у невырожденных матриц и только у них.
Доказательство. Пусть матрица А – невырожденная, т. е. 
. Тогда существует матрица
,
где 
– алгебраическое дополнение элемента 
, определяемое как = 
, где 
– минор элемента . Покажем, что матрица В является обратной для А, т. е. матрица С=АВ является единичной.
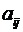
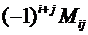
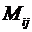
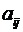
поскольку матрица 
имеет две одинаковых строки 
. Таким образом, С=Е.■
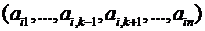
Одним из способов вычисления обратной матрицы является следующий.
1. Составить расширенную матрицу (А|Е), приписав после матрицы А за вертикальной чертой единичную матрицу той же размерности, что и А.
2. Матрицу (А|Е) с помощью элементарных преобразований строк привести к ступенчатому виду Гаусса.
Если при этом на месте матрицы А получилась матрица Е, то за вертикальной чертой находится матрица . В противном случае 
и матрица не существует.
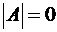
Сложение и вычитание матриц
Формула
Более подробно формула сложения двух матриц выглядит так:
В формуле складываются матрицы 3 на 3, значит и получиться должна матрица 3 на 3.
Запишем подробную формулу вычитания двух матриц:
Стоит так же заметить, что нельзя складывать и вычитать матрицы с обычными числами, а так же с другими какими-то элементами
Будет полезно знать для дальнейших решений задач с матрицами знать свойства сложения (вычитания).
Свойства
Примеры решений
Выполнить сложение матриц, а затем вычитание.
Аналогично сумме находим разность матриц с помощью замены знака «плюс» на «минус»:
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Найти сумму и разность матриц.
Как обычно сначала проверяем матрицы на одинаковую размерность.
Видим, что размерности двух матриц не совпадают, поэтому по определению суммы и разности матриц операции провести не возможно! На этом заканчиваем решение данного примера и записываем ответ.
В статье: «Сложение и вычитание матриц» были даны определения, правила, замечания, свойства операций и практические примеры решения.
Что называется суммой двух матриц
Матрицей 
размерности m×n называется таблица чисел aij, содержащая m строк и n столбцов. Числа aij называются элементами этой матрицы, где i – номер строки, j – номер столбца, на пересечении которых стоит данный элемент. Матрица, содержащая m строк и n столбцов, имеет вид:
Виды матриц:
1) при m=n – квадратная, в данном случае n называют порядком матрицы;
2) квадратная матрица, у которой все недиагональные элементы равны нулю – диагональная;
3) диагональная матрица, у которой все диагональные элементы равны единице – единичная и обозначается E;
4) при n≠m – прямоугольная;
5) при m=1 – матрица-строка (вектор-строка);
6) при n=1 – матрица-столбец (вектор-столбец);
7) при всех aij =0 – нулевая матрица.
Заметим, что основной числовой характеристикой квадратной матрицы является ее определитель. Определитель, соответствующий матрице n-го по-порядка, также имеет n-ый порядок.
Дадим ряд необходимых определений.
Определителем матрицы 2-го порядка называется число
Минором Мij элемента aij матрицы n-го порядка А называется определитель матрицы (n-1)-го порядка, полученной из матрицы А путем вычеркивания i-ой строки и j-го столбца.
1. При транспонировании матрицы ее определитель не меняется.
2. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак.
3. Определитель, имеющий две пропорциональные (равные) строки (столбца), равен нулю.
4. Общий множитель элементов какой-либо строки (столбца) определителя можно вынести за знак определителя.
5. Если элементы какой-либо строки (столбца) определителя представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
6. Определитель не изменится, если к элементам любой его строки (столбца) прибавить соответствующие элементы другой его строки (столбца), предварительно умноженные на любое число.
7. Определитель матрицы равен сумме произведений элементов любой его строки (столбца) на алгебраические дополнения этих элементов.
Поясним данное свойство на примере определителя 3-го порядка. В данном случае свойство 7 означает, что
Свойство 7 представляет собой теорему о разложении определителя, сформулированную Лапласом.
8. Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения соответствующих элементов другой его строки (столбца) равна нулю.
Последнее свойство часто называют псевдоразложением определителя.
Матрицы. Виды матриц
Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.
Матрица порядка m × n записывается в форме:
или 
(i=1,2. m; j=1,2. n).
Числа aij входящие в состав данной матрицы называются ее элементами. В записи aij первый индекс i означает номер строки, а второй индекс j— номер столбца.
Матрица строка
Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:
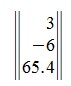
Матрица столбец
Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например
Нулевая матрица
Квадратная матрица
Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:
Главная диагональ матрицы
Побочная диагональ матрицы
Диагональная матрица
Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:
Единичная матрица
След матрицы
Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:
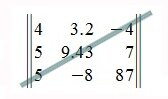
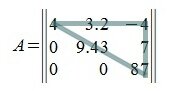
Верхняя треугольная матрица
Нижняя треугольная матрица
Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. aij=0, при всех i T ).
Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).
Ядро или нуль пространство матрицы
Противоположная матрица
Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.
Кососимметричная (Кососимметрическая) матрица
Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:
В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.
Пример кососимметрической матрицы:
Разность матриц
Разностью C двух матриц A и B одинакового размера определяется равенством
Для обозначения разности двух матриц используется запись:
Степень матрицы
Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:
где E-единичная матрица.
Из сочетательного свойства умножения следует:
где p,q— произвольные целые неотрицательные числа.
Симметричная (Симметрическая) матрица
Матрица, удовлетворяющая условию A=A T называется симметричной матрицей.
Для симметричных матриц имеет место равенство: