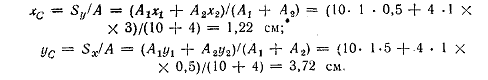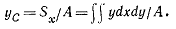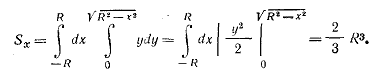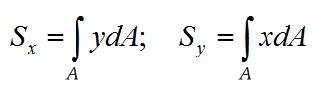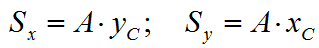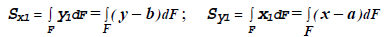Что называется статическим моментом сечения

СОПРОМАТ ОН-ЛАЙН

Меню сайта

Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое).

Базовый курс лекций по сопромату, теория, практика, задачи.

1. Геометрические характеристики сечений.

1.1. Статический момент сечения.

При дальнейшем изучении вопросов прочности, жесткости и устойчивости нам придется иметь дело с некоторыми геометрическими характеристиками сечения: статическими моментами, моментами инерции, моментами сопротивления.

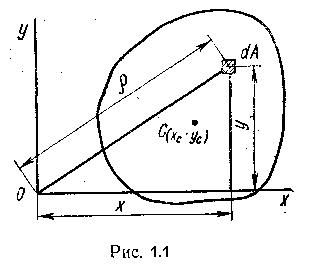
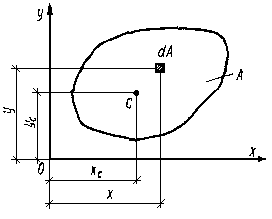
Статическим моментом Sx сечения (фигуры) относительно какой-либо оси х (рис.1.1) называется геометрическая характеристика, определяемая интегралом вида

(1.1)

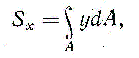
Единицей измерения статического момента является единица длины в третьей степени, обычно см 3 (см в третьей степени). Статический момент может быть положительным, отрицательным и, в частности, равным нулю. Если отождествить площадь с силой, действующей перпендикулярно плоскости чертежа, то интеграл (4.1) можно рассматривать как сумму моментов сил относительно оси х. По известной из теоретической механике теореме о моменте равнодействующей можно написать

(1.2)

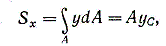
Из формулы (1.2) следует формула определения ординаты центра тяжести

Аналогично, статический момент относительно оси у равен

(1.4)

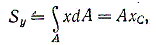
Центр тяжести обладает тем свойством, что если тело опереть в этой точке, то оно будет находиться в равновесии.

Из формулы (1.2) и (1.4) следует, что если оси х и у проходят через центр тяжести фигуры, то статический момент относительно этих осей равен нулю. Такие оси называются центральными осями.

Если фигуру можно представить в виде отдельных простых фигур (квадратов, треугольников и т.д.), для которых известны положения центров тяжести, то в этом случае статический момент всей фигуры можно получить как сумму статических моментов этих простых фигурю Это непостредственно следует из свойств определенного интеграла.

Если фигура имеент ось симметрии, то последняя всегда проходит через центр тяжести фигуры, а потому статический момент фигуры относительно оси симметрии всегда равен нулю.

Во многих случаях вместо простых интегралов вида (1.1) и (1.4) удобнее иметь дело с двойными интегралами вида:

(1.1a)

(1.4a)

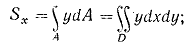
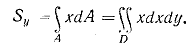
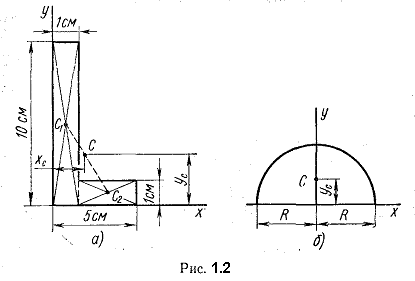
Пример 1.1. Определить положение центра тяжести сечения, показанного на рис. 1.2, а.

Решение. Разбиваем сечение на два прямоугольника. Проводим вспомогательные оси х и у.

По формулам (1.3) и (1.5) получим:

Пример 1.2. Вычислить ординату центра тяжести половины круга (рис. 1.2, б).

Решение. Пользуемся формулой

Вычисляем числитель, используя уравнение окружности х 2 + y 2 = R 2 :

Полезные ссылки

Источник

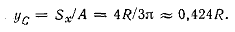
iSopromat.ru

Формулы для расчета геометрической характеристики статического момента сечений, плоских фигур и площади:

Рассмотрим сечение (плоскую фигуру) произвольной формы площадью A:

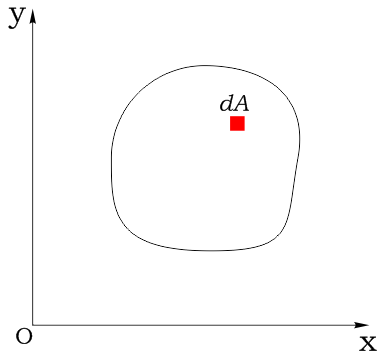
Выделим в нем элементарную площадку dA и зададим систему координат:

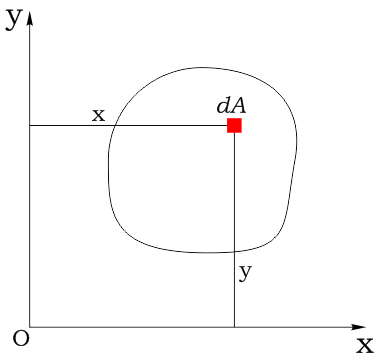
Координаты площадки обозначим соответственно как x и y:

Статический момент элементарной площадки:

Суммируя выражения по всей площади фигуры, получим соответственно:

Единица измерения статического момента [м 3 ].

тогда статические моменты относительно осей x и y:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Набор студента для учёбы

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Источник

Статические моменты плоских сечений

Площадь стержня.

При расчетах элементов конструкций используются различные геометрические характеристики. Так, например, при растяжении и сжатии используется площадь поперечного сечения стержня. Она применяется при определении напряжений и деформаций растянутого или сжатого стержня, т.е. чем больше площадь поперечного сечения тем большую нагрузку сможет выдержать стержень.

Оказывается, при других деформациях эта геометрическая характеристика не является достаточной. Необходимо использовать другие, более сложные геометрические характеристики.

Статические моменты плоских сечений

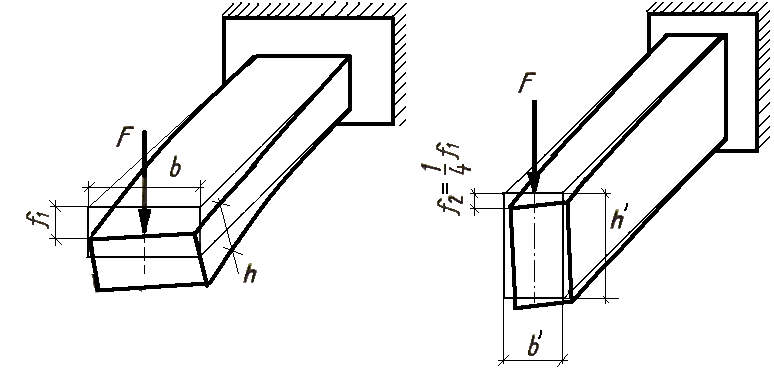
Нетрудно убедиться, что в случае изгиба бруса площадь се­чения не может служить характеристикой его жесткости. Дей­ствительно, из двух брусьев (рис. 2.2.1) с равновеликими площа­дями поперечных сечений первый при данной нагрузке деформируется значительно сильнее второго (например, при h/b = 2 прогибы первого бруса в четыре раза больше, чем второго).

Следовательно, при одной и той же площади поперечного сечения стержня, но при разном расположении его стержень сопротивляется изгибу по разному. Это позволяет сделать вывод о том, что площадь поперечного сечения не может характеризовать сопротивляемость стержня изгибу и при изучении изгиба приходится вводить другие геометрические характеристики — статический момент площади (сечения).

Выполняя расчеты на прочность, необходимо бывает вычислять статические моменты всего сечения или части его относительно некоторых осей.

Рассмотрим произвольное поперечное сечение стержня в системе координат х,у, выдел элементарную площадку dА (рис. 2.2.2)

Статическим моментом сечения относительно данной оси называется сумма произведений элементарных площадей dА, на их расстояния до данной оси (например, х или у), которая распространяется на всю площадь сечения А.

Так, статические моменты сечения относительно осей х и у равны:

; (2.2.1)

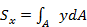
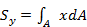
Ось, относительно которой статический момент равен нулю, называется центральной.

Точка пересечения центральных осей называется центром тяжести сечения.

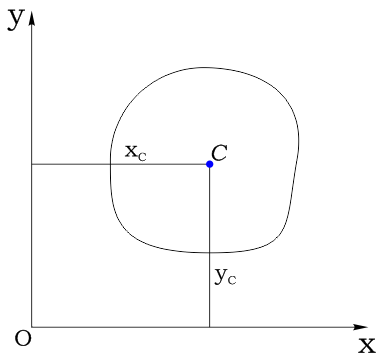
Можно показать, что и относительно любой оси, проходящей через центр тяжести сечения, статический момент равен нулю. Для изображенного на рис. 2.2.2 сечения центр тяжести располагается в точке С, его координатами являются ординаты х_с и у_с. Все оси, которые проходят через эту точку, будут центральными и относительно таких осей статический момент равен нулю.

На основании теоремы Вариньона следует, что

; (2.2.2)

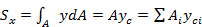
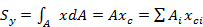
Следовательно, статический момент площади А относительно какой-либо оси равен произведению всей площади на расстояние от ее центра тяжести до этой оси.

Из выражений (2.2.2) получим формулы для определения координат центра тяжести сечения:

; (2.2.3)

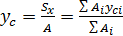
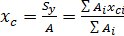
Заметим, что последняя форма записи в выражениях (2.2.3) относится к определению координат центра тяжести сложного сечения разбитого на простейшие составные части, для которых известны площади А и положение центра тяжести и у_с

Для большинства сечений определение положения центра тяжести упрощается. Так, если сечения имеют ось или центр симметрии, то центр тяжести в таких сечениях находится соответственно на оси симметрии или в центре симметрии.

Дата добавления: 2016-01-18 ; просмотров: 2913 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

СОПРОМАТ ОН-ЛАЙН

Меню сайта

Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое).

Базовый курс лекций по сопромату, теория, практика, задачи.

1. Геометрические характеристики сечений

1.1. Статический момент сечения

Статические моменты сечения Sx и Sy используются главным образом для определения положения центра площади сечения и центральных осей.

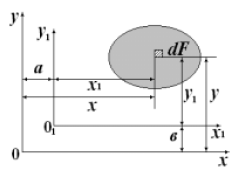
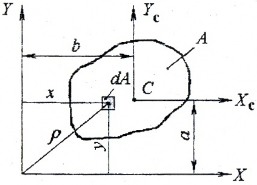
Рассмотрим изменение статических моментов при параллельном переносе осей (рис. 1.1). Считая известными F, Sx и Sy в системе координат 0XY определим статические моменты S_x1, S_y1 относительно новых осей x₁, y₁.

Рис. 1.1

Оси x₁, y₁ можно выбрать таким образом, чтобы выполнились условия:

Оси, относительно которых статические моменты сечения равны нулю, называются центральнми. Точка пересечения центральных осей называется центром тяжести сечения.

Принимая S_x1 = 0 и S_y1 = 0, из выражения (1.1) координаты центра площади сечения относительно вспомогательных осей x, y определяются по формулам (обозначим x_c = a, y_c = b):

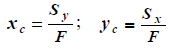(1.2)

Соответственно, если площадь F и положение центра площади сечения (координаты x_c, y_c) в системе координат 0xy известны, то статические моменты сечения относительно осей x, y можно определить из выражений (1.2):

Можно показать, что статический момент относительно любой оси, проходящей через центр площади сечения, равен нулю.

При определении центра площади сложного сечения применяется следующая процедура:

1) сечение разбивается на n частей, площади (F_i) и положение центров (C_i) площади которых известны;

2) задается вспомогательная система координат, в которой определяются координаты центров площадей (x_ci, y_ci) этих частей;

3) вычисляются координаты составного сечения по формулам:

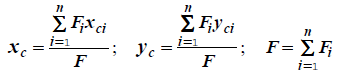(1.4)

Пример 1. Выполнен с помощью он-лайн программы. (перейдя к примеру нажмите на одно из действий в блоке-меню «Расчет»)

Источник

iSopromat.ru

Рассмотрим формулы для определения геометрических характеристик плоских сечений: статического момента площади фигуры, осевых моментов инерции и радиуса инерции сечения.

При расчете элементов конструкций на прочность, жесткость и устойчивость приходится кроме общеизвестной характеристики – площади поперечного сечения A, оперировать такими геометрическими характеристиками сечений, как статический момент площади, момент инерции, момент сопротивления, радиус инерции.

Статический момент площади

Интегралы вида:

называются статическими моментами площади сечения A относительно осей X и Y соответственно.

В тех случаях, когда сечение может быть разделено на простейшие фигуры площади A_i и координаты центров тяжести x_i и y_i которых известны, статические моменты площади сложной фигуры определяются через суммирование

Статические моменты площади имеют размерность [м 3 ] и могут принимать любые числовые значения. Для осей X_C, Y_C, проходящих через центр тяжести сечения C (центральные оси), статические моменты равны нулю:

Координаты центров тяжести сечения определяются относительно так называемых вспомогательных осей по формулам: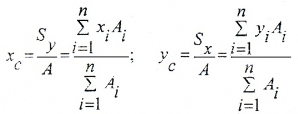

Если сечение имеет ось симметрии, то центр тяжести находится на этой оси и его положение определяется одной координатой.

При наличии двух и более осей симметрии центр тяжести совпадает с точкой пересечения этих осей.

Моменты инерции

Моментами инерции площади сечения называют интегралы вида: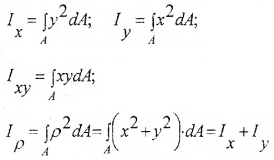

где:
I_x, I_y — осевые моменты инерции площади сечения относительно осей OX, OY соответственно;
I_xy — центробежный момент инерции;
I_ρ — полярный момент инерции.

Размерность момента инерции [м 4 ], I_x, I_y, I _ρ всегда положительны, I_xy может принимать любые значения, при этом, если хотя бы одна из осей является осью симметрии, I_xy=0.

Зависимости между моментами инерции относительно параллельных осей выражаются формулами:

где a, b – расстояния между осями X, X_C и Y, Y_C.

Оси, относительно которых I_xy=0, называют главными, а осевые моменты инерции относительно них – главными моментами инерции.

Главные оси, проходящие через центр тяжести сечения, называют главными центральными осями, а соответствующие им моменты инерции – главными центральными моментами инерции.

Главные оси характерны тем, что их моменты инерции принимают экстремальные значения (I_max, I_min).

Момент инерции сложного сечения относительно какой-либо оси находится суммированием моментов инерции составляющих его частей относительно той же оси:

Радиусы инерции

Величины

называют радиусами инерции сечения относительно осей OX и OY соответственно.

Эллипс, построенный в главных осях, с полуосями, равными главным радиусам инерции

называют эллипсом инерции.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник