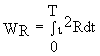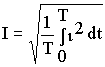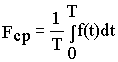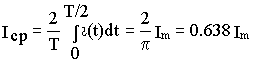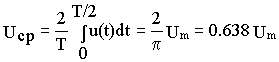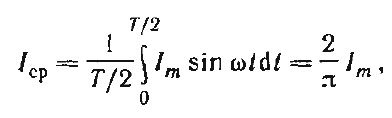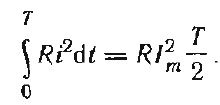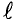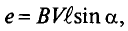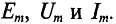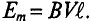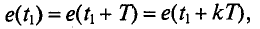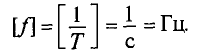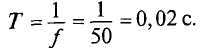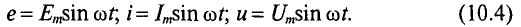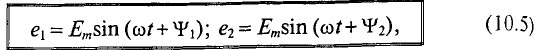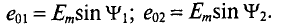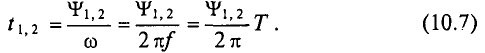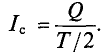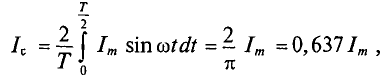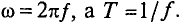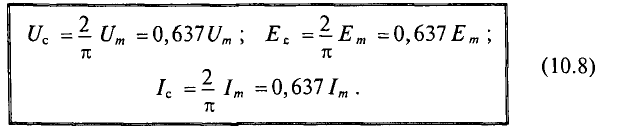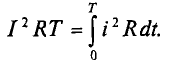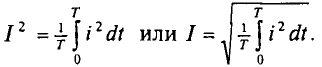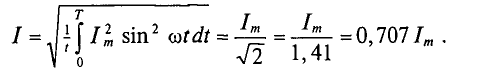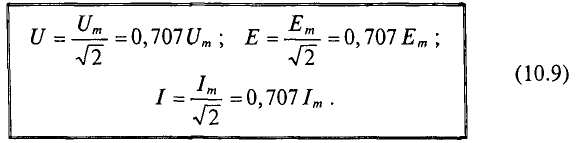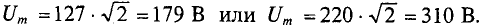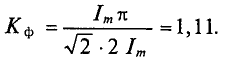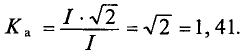Что называется средним значением переменного синусоидального тока
Действующее и среднее значения переменного тока
Основной задачей расчета электрической цепи является определение тока. В цепях постоянного тока, если нет регулирующих устройств, ток остается неизменным и его легко рассчитать или измерить. В цепях переменного тока ток непрерывно меняется по величине и по направлению. Если, допустим, что каким-либо путем нам удалось определить одно мгновенное значение тока, то это не даст оценки действия всех остальных значений.
Поэтому переменный ток оценивается по его действию, которое эквивалентно действию некоторого постоянного тока. В качестве критерия такой эквивалентности принято считать тепловое действие тока.
Действующее значение переменного тока численно равно такому постоянному току, который в элементе цепи за время, равное периоду Т, выделяет такое же количество тепла, какое в том же элементе за то же время при тех же условиях выделяет переменный ток.
Определим количество тепла, которое выделяется за период Т постоянным током.
По закону Джоуля – Ленца:



Для переменного тока

По определению количество тепла, выделяемое постоянным и переменным токами, должно быть одинаково.


Тогда действующее значение тока определится выражением

Полученное выражение справедливо для любого переменного тока независимо от его формы.
Определим действующее значение синусоидального тока. Представим мгновенное значение тока в виде 

Используя правила тригонометрических преобразований, выразим


Отсюда 

Действующее значение синусоидального тока в 
То же самое можно сказать о напряжении и ЭДС:


Действующие значения токов, напряжений и ЭДС обозначаются прописной буквой без индекса. Все расчеты в цепях переменного тока выполняются для действующих значений токов, напряжений и ЭДС.
Действующее значение переменного тока можно измерить приборами любой системы, кроме магнитоэлектрической.
Отношение амплитуды к действующему значению тока называется коэффициентом амплитуды.
Для синусоидальных токов коэффициент амплитуды всегда равен 

В ряде случаев при анализе электрических цепей переменного тока необходимо определить среднее значение переменного тока.
Средним значением переменного тока называется среднее арифметическое из всех мгновенных значений за половину периода.
Для синусоидальных величин среднее значение всегда оценивается за половину периода, так как мгновенные значения полпериода положительны, а полпериода – отрицательны, в результате среднее значение за период равно нулю.
Найдем среднее значение переменного тока:

Учтем, что 

Отношение действующего значения к среднему называется коэффициентом формы кривой.

Учтем, что 

Подставив эти значения в формулу коэффициента формы, получим для синусоидального тока

Таким образом, действующие значения тока, напряжения и э.д.с. связаны со средними значениями соотношениями:



Что называется средним значением переменного синусоидального тока
Основные характеристики синусоидальных электрических величин. Мощность в цепи синусоидального тока.
Из всех возможных форм периодических токов и напряжений наибольшее распространение получили синусоидальные. По сравнению с другими синусоидальные токи и напряжения имеют то преимущество, что позволяют наиболее экономично осуществлять производство, передачу на расстояние и использование электрической энергии. Только при помощи синусоидальных токов удается сохранить неизменными формы кривых токов и напряжений на всех участках линейной ЭЦ.
В настоящее время производство и передача электрической энергии в во всех европейских странах (включая Россию) осуществляется при помощи трехфазного синусоидального тока с частотой 50 Герц, В СЩА и Японии- с частотой 60 Гц.
Различные области техники используют весьма широкий диапазон частот в зависимости от технических потребностей. В авиации, например, успешно применяется синусоидальный ток с частотой 400 Гц, т.к. при такой частоте снижаются габаритные размеры и вес авиационного оборудования. В электротехнологических установках используют диапазон от 500 Гц до 50 мГц. Частоты от нескольких сотен мегагерц до миллиарда Гц применяют в радиотехнике.
Мгновенные, средние и действующие значения синусоидальных напряжений и токов.
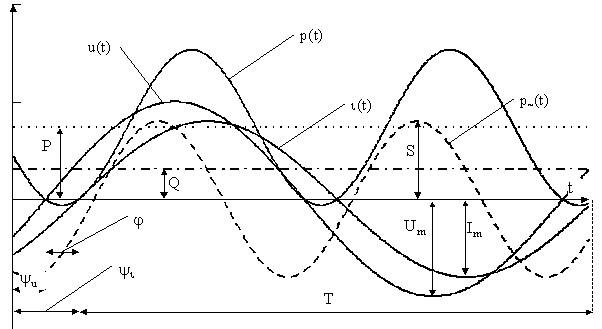
Синусоидальные напряжения и токи представляют собой величины, изменяющиеся во времени по синусоидальному закону (см. рис.2.1), т.е.
i (t)= I m Sin ( w t+ y i ), А,
Время, за которое совершается одно полное коленбание, называется периодом Т.
Число периодов в секуду называется частотой (f) и измеряется в Герцах, т.е.
Аргумент синусоидальной функции
измеряемый в угловых единицах (радианах или градусах) называется фазой синусоиды. Фаза линейно растет во времени со скоростью
которая называется угловой частотой.
При совместном рассмотрении двух синусоидально изменяющихся величин одинаковой частоты вводится понятие фазового сдвига между ними.
Так фазовый сдвиг j между напряжением и током равен разности начальных фаз напряжения и тока, т.е.
Если j >0, то напряжение опережает по фазе ток; если j j =0, то напряжение совпадает по фазе с током.
Для оценки эффективности действия периодического тока используют его тепловое или электродинамическое действие и сравнивают с анало-гичным действием постоянного тока за один и тот же интервал времени, равный периоду тока Т.
Энергия, преобразуемая в тепло в резистивном элементе с сопротивлением R за время “Т” при протекании через него постоянного тока I определяется выражением
За то же время в том же элементе при протекании периодического тока i (t) в виде тепла выделится энергия
Из равенства энергий найдем действующее значение периодического тока как
I=Im/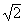
Аналогично находится действующее значение синусодального напряжения.
U=Um/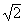
Для измерения действующих значений напряжений и токов применяется тепловая, электромагнитная, электродинамическая и другие системы приборов. Шкалы этих приборов проградуированы в в действующих значениях и для определения амплитуды синусоидального напряжения или токм надо показания прибора умножить на 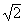
Для синусоидальной функции времени среднее за период значение равно 0, т.к. площадь отрицательной полуволные компенсируется площадью положительной полуволны. Поэтому для характеристики синусоидальной во времени величины используется понятие среднего полупериодного значения, соответствующего положительной полуволне синусоиды. Таким образом среднее значение синусоидального тока равно
Аналогично, среднее значение синусоидального напряжения определяется как
Мощность в цепях синусоидального тока.
Для характеристики мощности в цепи синусоидального тока используются понятия мгновенной, активной, реактивной и полной мощности.
Мгновенная мощность, характеризующая скорость изменения энергии в цепи в любой момент времени определяется выражением
Как видно, выражение для мгновенной мощности содержит постоянную составляющую p = и переменную составляющую p
, меняющуюся с удвоенной частотой относительно частоты изменения напряжения и тока.
Среднее за период “Т” значение мощности, определяемое интегралом
называется активной мощностью. Эта мощность, характеризует энергию, рассеиваемую за период питающего напряжения в виде тепла в резистивных элементах цепи и измеряется в ваттах. Видно, что средняя или активная мощность всегда положительна и равна постоянной составляющей мгновенной мощности.
При расчетах электрических цепей и на практике используется понятие реактивной мощности Q, которая вычисляется по формуле
Величина S, равная произведению действующих значений тока и напряжения на зажимах ЭЦ, называется полной или кажущейся мощностью и измеряется в вольт-амперах (ВА).
Полная мощность равна амплитуде переменной составляющей мгновенной мощности (см.рис.2.1).
При расчетах мощностей в цепях переменного тока пользуются понятием коэффициента мощности
который характеризует долю средней или активной мощности P в полной мощности S. Чем меньше Cos j при одинаковой активной мощности Р, тем больше ток и потери в устройствах передачи энергии. Повышение коэффициента мощности промышленных установок представляет собой важную народно-хозяйственную задачу.
На щитке любого источника переменного тока (генератора или трансформатора) указывается значение полной мощности S, представляющей предельную мощность установки. Только при Cos j =1, т.е. при совпадении начальных фаз тока и напряжения, активная мощность становится равной полной мощности и, следовательно, мощность источника используется полностью.
Среднее и действующее значения синусоидально изменяющейся величины
Среднее значение
Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за полпериода.
Среднее значение тока:
т. е. среднее значение синусоидального тока составляет 2/π = 0,638 от амплитудного. Аналогично, Eср = 2Ем/π ; Ucp = 2Uм/π.
Действующее значение
Широко применяют понятие действующего значения синусоидально изменяющейся величины (его называют также эффективным или среднеквадратичным).
Действующее значение тока:
Следовательно, действующее значение синусоидального тока равно 0,707 от амплитудного. Аналогично
Можно сопоставить тепловое действие синусоидального тока с тепловым действием постоянного тока, текущего то же время по тому же сопротивлению.
Количество теплоты, выделенное за один период синусоидальным током,
Выделенная за то же время постоянным током теплота равна RI 2пост Т. Приравняем их:
Таким образом, действующее значение синусоидального тока I численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.
Большинство измерительных приборов показывает действующее значение измеряемой величины.
Однофазные электрические цепи переменного тока
Содержание:
Однофазные электрические цепи переменного тока:
Для получения, передачи и распределения электрической энергии применяются в основном устройства переменного тока: генераторы, трансформаторы, линии электропередачи и распределительные цепи переменного тока.
Постоянный ток, необходимый в некоторых областях народного хозяйства (транспорт, связь, электрохимия и др.), получают выпрямлением переменного тока.
Переменным электрическим током называют ток, периодически изменяющийся по величине и направлению.
Основное достоинство переменного тока заключается в возможности трансформировать напряжение. Кроме того, электрические машины переменного тока надежней в работе, проще по устройству и эксплуатации.
Говоря о переменном токе, обычно имеют в виду синусоидальный переменный ток, т. е. ток, изменяющийся по синусоидальному закону. При синусоидальном токе ЭДС электромагнитной индукции, самоиндукции и взаимоиндукции изменяются по синусоидальному закону.
Синусоидальный переменный ток проходит в замкнутой линейной электрической цепи под действием синусоидальной ЭДС.
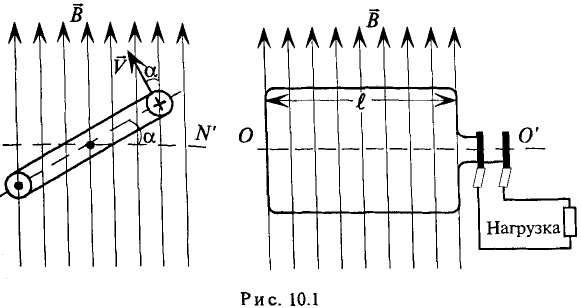
Рассмотрим получение синусоидальной ЭДС. Если в однородном магнитном поле с индукцией В равномерно со скоростью V вращается рамка (рис. 10.1), то в каждой активной стороне этой рамки длиной
Плоскость 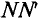
как 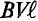
Синусоидальная ЭДС 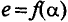
Величины, характеризующие синусоидальную ЭДС
Амплитуда — это максимальное значение периодически изменяющейся величины.
Обозначаются амплитуды прописными буквами с индексом m, т. е.
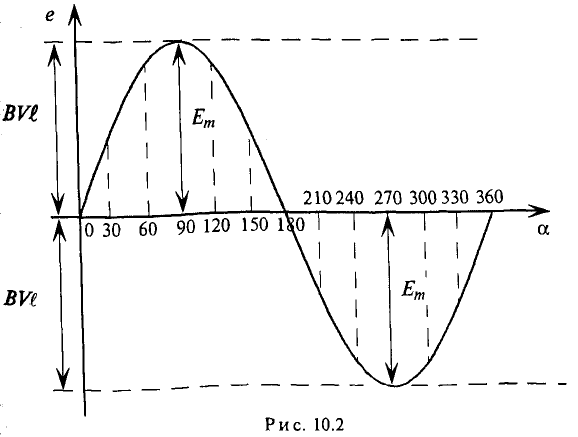
Нетрудно видеть (рис. 10.2), что ЭДС достигает своих амплитудных значений тогда, когда рамка повернется на угол а = 90° или на угол а = 270°, так как 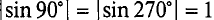
Тогда
Обозначается период буквой Т и измеряется в секундах, с (сек) т.е. 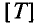
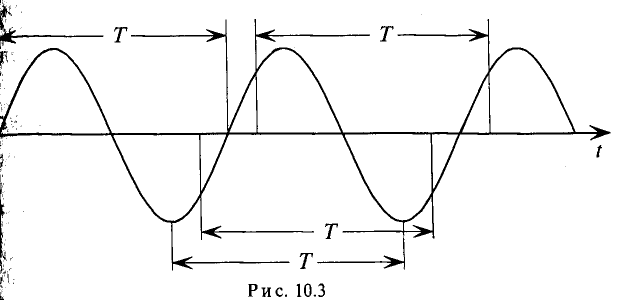
Значение ЭДС через каждый период определяется следующим равенством (рис. 10.3):
На рис. 10.3 изображена временная диаграмма синусоидальной ЭДС при вращении рамки в магнитном поле.
Обозначается частота буквой 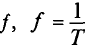
При частоте 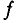
Угловая частота (угловая скорость) характеризуется углом поворотом рамки в единицу времени.
Обозначается угловая частота буквой 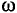
Измеряется угловая частота в единицах радиан в секунду, так как угол измеряется в радианах (рад).
Так, время одного периода Т рамка повернется на угол 360° = рад. Следовательно, угловую частоту можно выразить следующим образом:
Мгновенное значение — это значение переменной величины в й конкретный момент времени.
Мгновенные значения обозначаются строчными буквами..
Из выражения (10.2) следует, что угол поворота рамки 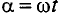
Таким образом, любая синусоидальная величина характеризуется амплитудой и угловой частотой, которые являются постоянными для данной синусоиды. Следовательно, по формулам (10.4) можно определить синусоидальную величину в любой конкретный момент времени t, если известны амплитуда и угловая частота.
Фаза и сдвиг фаз
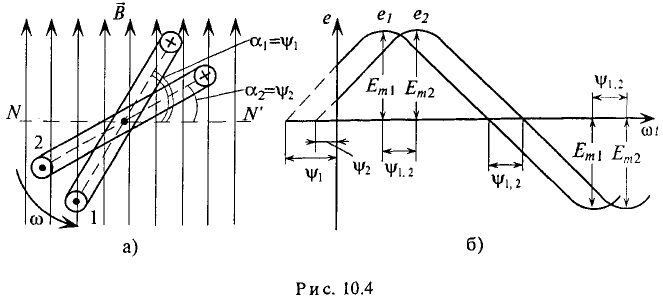
Если в магнитном поле вращаются две жестко скрепленные между собой под каким-то углом одинаковые рамки (рис. 10.4а), т.е. амплитуды ЭДС 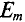
где 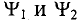
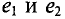
Поэтому эти углы 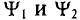
Начальные фазы 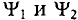
Таким образом, согласно (10.5) каждая синусоидальная величина характеризуется амплитудой 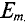

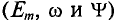


Величина 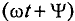
Разность начальных фаз двух синусоидальных величин одинаковой частоты определяет угол сдвига фаз этих величин:
При вращении против часовой стрелки (рис. 10.4а) ЭДС в первой рамке достигает амплитудного и нулевого значения раньше, чем во второй, т. е. 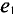
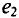
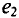
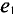
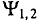
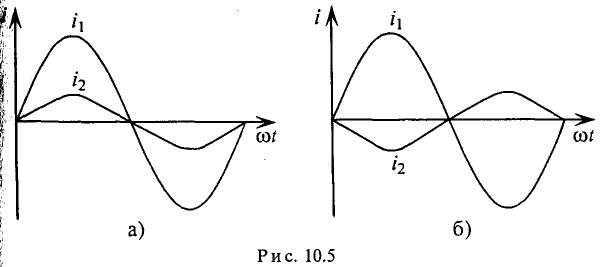
Две синусоидальные величины одинаковой частоты, достигаю-одновременно своих амплитудных (одного знака) и нулевых сечений, считаются совпадающими по фазе (рис. 10.5а).
Если две синусоиды одинаковой частоты достигают одновременно своих нулевых и амплитудных значений разных знаков (рис. 10.56), то они находятся в противофазе.
Время, на которое одна синусоидальная величина опережает и отстает от другой, характеризует время сдвига фаз 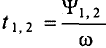
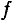
Среднее и действующее значения переменного тока
Кроме амплитудных и мгновенных значений переменный ток, напряжение, ЭДС характеризуются еще средними и действующими (эффективными) значениями.
Среднее значение переменного тока
Среднее значение переменного тока равно величине такого постоянного тока, при котором через поперечное сечение провод-проходит то же количество электричества Q, что и при переменном токе.
Таким образом, среднее значение переменного тока эквивалентно постоянному току по количеству электричества Q, проходящему через поперечное сечение проводника в определенный промежуток времени.
Средние значения переменных величин обозначаются прописными буквами с индексом «с», т. е. 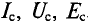
Если ток изменяется по синусоидальному закону, то за половину периода через поперечное сечение проводника проходит определенное количество электричества Q в определенном направлении, а за вторую половину периода через то же сечение проходит то же количество электричества в обратном направлении. Таким образом, среднее значение синусоидального тока за период равно нулю, т. е. 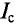
Поэтому для синусоидального переменного тока определяется его среднее значение за половину периода Т/2, т. е.
Из выражения (2.1) значение переменного тока 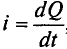
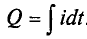
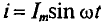
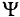
где
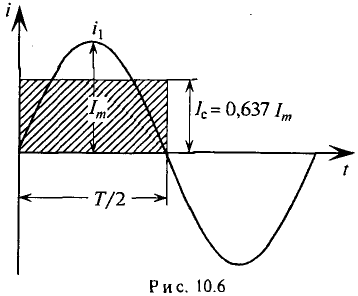
Графически среднее за полупериод значение синусоидального тока равно высоте прямоугольника с основанием, равным Т/2, и площадью, равной площади, ограниченной кривой тока и осью абсцисс за половину периода (рис. 10.6).
Под средним значением переменной величины понимают постоянную составляющую этой величины.
Средние значения синусоидального напряжения и ЭДС за полупериод можно определить по аналогии с током.
Действующее значение переменного тока
Действующее (или эффективное) значение переменного тока — значение переменного тока, эквивалентное постоянному току тепловому действию.
Действующее значения переменных величин обозначается прочими буквами без индексов: I, U, Е.
Действующее значение переменного тока I равно величине такого постоянного тока, которое за время, равное одному периоду первого тока Т, выделит в том же сопротивлении R такое же количество тепла, что и переменный ток i:
Откуда действующее значение переменного тока
Если переменный ток изменяется по синусоидальному закону с начальной фазой, равной нулю, т.е. 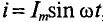
Номинальные значения тока и напряжения в электрических цепей и устройствах выражаются их действующими значениями.
Так, например, стандартные напряжения электрических сетей U= 127 В или U = 220 В выражают действующие значения этих напряжений. А изоляцию необходимо рассчитывать на амплитудное значение этих напряжений, т. е.
При расчете цепей переменного тока и их исследованиях чаще всего пользуются действующими (эффективными) значениями тока, напряжения и ЭДС.
На шкалах измерительных приборов переменного тока указывается действующие значение переменного тока или напряжения.
Именно действующие значения тока, напряжения и ЭДС указываются в технической документации, если нет специальных оговорок.
Коэффициенты формы и амплитуды
Отклонения кривых тока, напряжения и ЭДС от синусоиды характеризуются коэффициентами формы 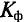
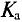
Коэффициент формы 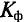
Коэффициент формы необходимо учитывать при проектировании и изучении выпрямительных устройств и электрических машин.
Для синусоидальных величин коэффициент формы будет равен
Коэффициент амплитуды 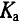
Для синусоидальных величин коэффициент амплитуды равен
Чем больше коэффициент формы и коэффициент амплитуды отличается от значений 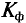
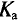
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.