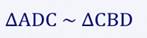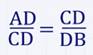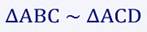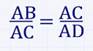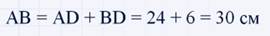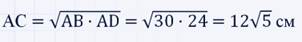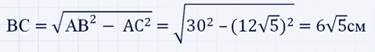Что называется средним пропорциональным для отрезков

Что такое средний пропорциональный?

Среднее пропорциональное Среднее пропорциональное между двумя положительными числами, число, равное квадратному корню из их произведения. Таким образом, если а: х = х: b, то x есть С. … х называется также геометрическим средним чисел а и b.

Что такое средний пропорциональный отрезок?

Отрезок ХУ называется средним пропорциональным (или средним геометрическим) для отрезков АВ и СD, если выполняется равенство: … Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла.

Как найти средний пропорциональный отрезок?

Пропорциональные отрезки в прямоугольном треугольнике

Какой отрезок называется средним пропорциональным?

Отрезок XY называется средним геометрическим (или средним пропорциональным) для отрезков, на которые делится гипотенуза этой высотой. … Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для проекций катетов на гипотенузу.

Для чего используют среднее геометрическое?

Геометрическое среднее (geometric mean) — наиболее часто используются для того, чтобы сосчитать среднее значение темпов роста, доходности и т. п. арифметическое дает представление о доходе за 1 период без усложнения доходностей. …

Что такое среднее геометрическое и среднее пропорциональное?

между двумя положительными числами, число, равное квадратному корню из их произведения. Таким образом, если а: х = х: b, то x есть С. чисел а и b и х называется также геометрическим средним чисел а и b. …

Как найти средний пропорциональный?

Среднее пропорциональное Среднее пропорциональное между двумя положительными числами, число, равное квадратному корню из их произведения. Таким образом, если а: х = х: b, то x есть С.

Как определить пропорциональность сторон?

Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то такие треугольники подобны.

Как найти гипотенузу если известен катет и его проекция?

Возведите высоту в квадрат и разделите на длину известной проекции: Ас = Н²/Вс. Если известна длина проекции одного из катетов (Вс) и длина гипотенузы (С), то способ нахождения длины проекции другого катета (Ас) — отнимите от второй известной величины первую: Ас = С-Вс.

Как найти гипотенузу в прямоугольном треугольнике?

Длина гипотенузы прямоугольного треугольника может быть найдена с помощью теоремы Пифагора: Квадрат длины гипотенузы равен сумме квадратов длин катетов.

Как найти высоту в прямоугольном треугольнике?

Примеры решения задач

Как найти катет в прямоугольном треугольнике?

Катет прямоугольного треугольника равен его гипотенузе, умноженной на синус противолежащего или на косинус прилежащего к этому катету угла.

Где используется среднее гармоническое?

В статистике среднее гармоническое применяется в случае, когда наблюдения, для которых требуется получить среднее арифметическое, заданы обратными значениями. В формуле тонкой линзы удвоенное фокусное расстояние равно среднему гармоническому расстояния от линзы до предмета и расстояния от линзы до изображения.

Для чего используется среднее гармоническое?

Среднее гармоническое помогает нам вычислить среднее арифметическое в рядах чисел, заданных обратными значениями. Это бывает чаще, чем можно подумать. Например, если я еду со скоростью 30 км/ч, это значит, что я получаю определённый результат (30 км) за какую-либо единицу времени (1 час).

Как вычислить среднее геометрическое арифметическое?

Чтобы найти среднее геометрическое, нужно перемножить все числа и извлечь из них корень. Степень корня определяется количеством чисел. Пример: Найти среднее геометрическое 2, 4 и 8.

Источник

Что называется средним пропорциональным для отрезков

Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту

В этом уроке познакомимся с понятием «среднее геометрическое» или «среднее пропорциональное» для отрезков, выведем формулы для вычисления высоты и катетов прямоугольного треугольника через понятие среднее пропорциональное, рассмотрим задачу на применение формул.

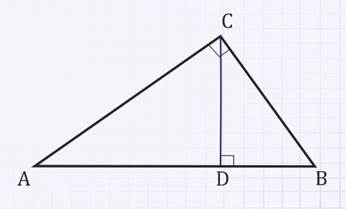
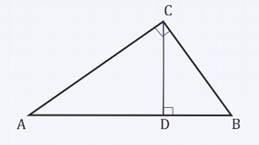
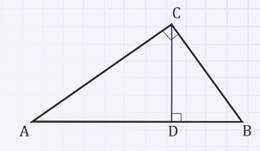
Доказать, что высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

∆АВС – прямоугольный треугольник,

СD – высота, проведенная из вершины С к гипотенузе АВ.

1)Рассмотрим треугольники АВС и АСD.

∠АСВ = ∠АDС = 90°, отсюда следует, что треугольники АВС и АСD подобны по первому признаку подобия треугольников, т.е. по двум равным углам.

2)Рассмотрим треугольники АВС и СВD.

∠АСВ = ∠ВDС = 90°, то треугольники АВС и СВD тоже подобны по первому признаку подобия треугольников. А раз так, то ∠А = ∠ВСD.

3)Рассмотрим треугольники АСD и СВD.

Так как ∠АDС = ∠СDВ = 90° и ∠А = ∠ВСD, то треугольники АСD и СВD подобны по первому признаку подобия треугольников.

Что и требовалось доказать.

В геометрии в формулировках ряда утверждений и при решении отдельных задач используется понятие «среднее пропорциональное отрезков» или «среднее геометрическое».

Отрезок ХУ называется средним пропорциональным (или средним геометрическим) для отрезков АВ и СD, если выполняется равенство:

Исходя из доказанной выше задачи, можно выделить два утверждения.

1.Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.

Для вывода данного утверждения воспользуемся доказанным, а именно, что:

Применяя основное свойство пропорции, получим

2.Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла.

Также по выше доказанному в задаче:

Решим задачу, применяя данные утверждения.

Найдите катеты прямоугольного треугольника АВС, если АD = 24 см, ВD = 6 см.

Найдем гипотенузу данного прямоугольного треугольника:

Теперь воспользуемся равенством второго утверждения:

Для вычисления второго катета воспользуемся теоремой Пифагора:

или равенством все того же второго утверждения:

Источник

Пропорциональные отрезки

Отрезки AB и CD пропорциональны отрезкам AB₁ и CD₁, если:

Отношением отрезков AB и CD называется отношение их длин, т.е. \( \frac . \)

Пример 1. На рисунке 1 заданы отрезки \( \small AB, \; CD, \; A_1B_1,\; C_1D_1. \) Определить, являются ли отрезки \( \small AB \) и \( \small CD \) пропорциональны отрезкам \( \small A_1B_1 \) и \( \small C_1D_1 \).

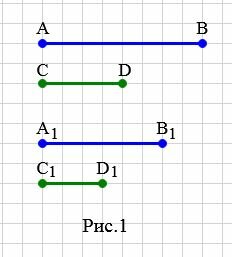Решение. Запишем длины отрезков:

.

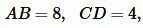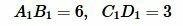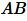
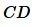
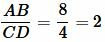Отношение отрезков и равно:

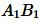
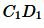
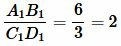Отношение отрезков и равно:

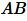
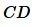
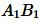
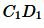
значит отрезки и пропорциональны отрезкам и .

Легко убедится, что выполяется также равенство (2) (это следует также из правила перекрестного умножения):

, .

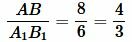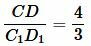Пример 2. На рисунке 2 заданы отрезки \( \small AB, \; CD, \; A_1B_1,\; C_1D_1. \) Определить, являются ли отрезки \( \small AB \) и \( \small CD \) пропорциональны отрезкам \( \small A_1B_1 \) и \( \small C_1D_1 \).

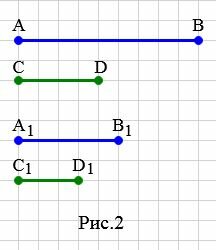Решение. Запишем длины отрезков:

.

, .

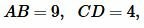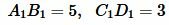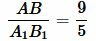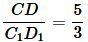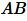
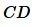
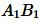
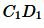
Следовательно отрезки и не пропорциональны отрезкам и .

Источник

Пропорциональные отрезки

Всего получено оценок: 313.

Всего получено оценок: 313.

Пропорциональные отрезки очень важны для определения подобия фигур. К тому же, правильно нареченные пропорционально рисунки помогают в правильном решении математических задач. Именно поэтому так важно разбираться в данной тематике.

Определение

Пропорциональными отрезками называются отрезки, у которых имеется постоянный коэффициент пропорциональности. Под коэффициентом пропорциональности понимается отношение длин отрезков.

Рис. 1. Пропорциональные отрезки.

Согласно определению пропорциональных отрезков, два отрезка всегда пропорциональны между собой, поскольку их длины не меняются со временем. Значит, не меняется и коэффициент пропорциональности.

Несмотря на это, чаще всего под пропорциональными отрезками понимают отрезки с коэффициентом кратным 0,5. Например, отрезки с коэффициентом 2,5, 1,5, 2 и тому подобные.

Пропорциональными будут являться и отрезки, составляющие подобные фигуры. Это действует в обе стороны. Если фигуры подобны, то их стороны пропорциональны, если все стороны пропорциональны, то фигуры подобны.

Подобные фигуры

Нужно понимать, что подобными фигурами могут быть не только треугольники, но вообще любые фигуры в геометрии, если все углы этих фигур равны, а длины сторон пропорциональны.

Рис. 2. Подобные фигуры.

Но при этом признаки подобия существуют только для треугольников. Их всего 3:

Пропорциональными могут быть только отрезки, как объекты имеющие длину. Прямая или луч бесконечны, а потому не могут быть подобными.

Пример

Решим небольшую задачу на пропорциональность отрезков. Имеется 3 пропорциональных отрезка. Каждый из которых больше предыдущего. Первый отрезок равен 5, третий 20. Необходимо найти длину второго отрезка.

Отрезки пропорциональны, значит отношение больших к меньшим будет постоянным. Обозначим неизвестны отрезок за х и решим уравнение.

Перенесем выражение из правой части в левую. Приведем получившееся выражение под один знаменатель и решим дробно-рациональное уравнение.

Что мы узнали?

Мы узнали, что такое пропорциональные отрезки. Выделили области, где могут быть применены навыки обращения с пропорциональными длинами и привели пример на заданную тему.

Источник

Пропорциональные отрезки в прямоугольном треугольнике

Разделы: Математика

Цели урока:

Тип урока: урок изучения нового материала.

План:

Ход урока

I. ОРГМОМЕНТ

– Здравствуйте ребята, присаживайтесь. Все готовы к уроку?

II. АКТУАЛИЗАЦИЯ ЗНАНИЙ

– С каким важным математическим понятием вы познакомились на предыдущих уроках? (с понятием подобия треугольников)

– Давайте вспомним, какие два треугольника называются подобными? (два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника)

– Чем мы пользуемся при доказательстве подобия двух треугольников? (признаки подобия треугольников)

– Сформулируйте эти признаки (формулируют три признака подобия треугольников)

III. ИЗУЧЕНИЕ СВОЙСТВА ВЫСОТЫ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА, ПРОВЕДЕННОЙ ИЗ ВЕРШИНЫ ПРЯМОГО УГЛА

а) подготовительный этап

– Ребята, посмотрите пожалуйста на первый слайд. (Приложение) Здесь изображены два прямоугольных треугольника – и . и – высоты и соответственно. .

Задание 1. а) Определите, подобны ли и .

– Что мы используем при доказательстве подобия треугольников? (признаки подобия треугольников)

– Какой признак подобия будем использовать и почему? (первый признак, т.к. в задаче ничего неизвестно о сторонах треугольников)

– Сколько пар равных углов нам нужно найти? Найдите эти пары. (Две пары: 1. ∟В= ∟В1 (прямые),2. ∟A= ∟A₁)

– Сделайте вывод.(по первому признаку подобия треугольников

)

Задание 1. б) Определите, подобны ли и .

– Какой признак подобия будем использовать и почему? (первый признак, т.к. в задаче ничего неизвестно о сторонах треугольников)

– Сколько пар равных углов нам нужно найти? Найдите эти пары (т.к. треугольники прямоугольные, то достаточно одной пары равных углов: ∟A= ∟A₁)

– Сделайте вывод. (по первому признаку подобия треугольников заключаем, что данные треугольники подобны).

В результате беседы слайд 1 выглядит так:

б) открытие теоремы

Задание 2.

– Определите, подобны ли и , и . В результате беседы выстраиваются ответы, которые отражены на слайде.

– На рисунке было указано, что . Использовали ли мы эту градусную меру при ответах на вопросы заданий? (Нет, не использовали)

– Ребята, сделайте вывод: на какие треугольники разделяет прямоугольный треугольник высота, проведенная из вершины прямого угла? (делают вывод)

– Возникает вопрос: а будут ли эти два прямоугольных треугольника, на которые высота разбивает прямоугольный треугольник, подобны между собой? Давайте попробуем найти пары равных углов.

В результате беседы выстраивается запись:

– А теперь давайте сделаем полный вывод.(ВЫВОД: высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному)

– Т.о. мы с вами сформулировали и доказали теорему о свойстве высоты прямоугольного треугольника.

Установим структуру теоремы и сделаем чертеж. Что в теореме дано и что нужно доказать? Учащиеся записывают в тетрадь:

– Докажем первый пункт теоремы для нового рисунка. Какой признак подобия будем использовать и почему? (Первый, т.к. в теореме ничего неизвестно о сторонах треугольников)

– Сколько пар равных углов нам нужно найти? Найдите эти пары. (В данном случае достаточно одной пары: ∟A-общий)

– Сделайте вывод. Треугольники подобны. В результате показывается образец оформления теоремы

– Второй и третий пункты распишите дома самостоятельно.

в) усвоение теоремы

– Итак, сформулируйте еще раз теорему (Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному)

– Сколько пар подобных треугольников в конструкции «в прямоугольном треугольнике проведена высота из вершины прямого угла» позволяет найти эта теорема? (Три пары)

Ученикам предлагается следующее задание:

IV. ВВЕДЕНИЕ ПОНЯТИЯ СРЕДНЕГО ПРОПОРЦИОНАЛЬНОГО ДВУХ ОТРЕЗКОВ

– А теперь мы изучим с вами новое понятие.

Определение. Отрезок XY называется средним пропорциональным (средним геометрическим) между отрезками AB и CD, если

(записывают в тетрадь).

V. УСВОЕНИЕ ПОНЯТИЯ СРЕДНЕГО ПРОПОРЦИОНАЛЬНОГО ДВУХ ОТРЕЗКОВ

– Теперь обратимся к следующему слайду.

Задание 1. Найдите длину среднего пропорционального отрезков MN и KP, если MN = 9 см, KP = 16 см.

– Что дано в задаче? (Два отрезка и их длины: MN = 9 см, KP = 16 см)

– Что нужно найти? (Длину среднего пропорционального этих отрезков)

– Какой формулой выражается среднее пропорциональное и как мы его найдем?

(Подставляем данные в формулу и находим длину ср.проп.)

Задание №2. Найдите длину отрезка AB, если среднее пропорциональное отрезков AB и СD равно 90 см и CD = 100 см

– Что дано в задаче? (длина отрезка CD = 100 см и среднее пропорциональное отрезков AB и СD равно 90 см)

– Что нужно найти в задаче? (Длину отрезка AB)

– Как будем решать задачу? (Запишем формулу среднего пропорционального отрезков AB и СD, выразим из нее длину AB и подставим данные задачи.)

VI. ВЫВОД СЛЕДСТВИЙ

– Молодцы, ребята. А теперь давайте вернемся к подобию треугольников, доказанному нами в теореме. Сформулируйте еще раз теорему. (Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному)

– Давайте вначале будем использовать подобие треугольников и . Что из этого следует? (По определению подобия стороны пропорциональны сходственным сторонам )

– Какое равенство получится при использовании основного свойства пропорции? ()

– Выразите СD и сделайте вывод (;.

Вывод: высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой)

– А теперь докажите самостоятельно, что катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой.

Доказывают самостоятельно, потом проверяем на слайде

VII. РЕШЕНИЕ ЗАДАЧ

Л.С. Атанасян «Геометрия 7-9», № 571(б)

– Прочитайте задачу. Что в задаче дано? (Дан прямоугольный )

– Что в задаче нужно найти? (Найти )

– Чем будет являться по отношению к и ? (Это среднее пропорциональное по следствию из доказанной теоремы)

– Как найти ? ()

– Как теперь найти ? (найдем из по теореме Пифагора: )

– Как найдем ? ( найдем из по теореме Пифагора: )

– Запишите ответ. (Ответ: )

VIII. ПОДВЕДЕНИЕ ИТОГОВ

– Подведем итог урока. С каким свойством высоты прямоугольного треугольника, проведенной из вершины прямого угла, мы сегодня познакомились? (Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному)

– Какое новое математическое понятие изучили? (Понятие среднего пропорционального двух отрезков.)

Высота прямоугольного треугольника, проведенная из вершины прямого угла есть среднее пропорциональное м/у…(-… отрезками, на которые делится гипотенуза этой высотой)

Катет прямоугольного треугольника есть среднее пропорциональное между…(-…гипотенузой и отрезком гипотенузы, заключенным между этим катетом и высотой)

– Где мы применяем изученные утверждения? (При решении задач)

IX. ПОСТАНОВКА ДОМАШНЕГО ЗАДАНИЯ

д/з: №571, №572 (а,д), самостоятельная работа в тетради, теория.

Источник