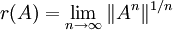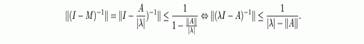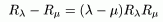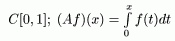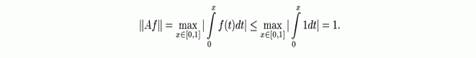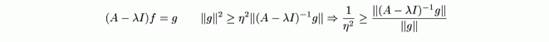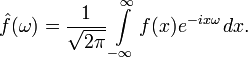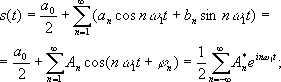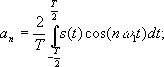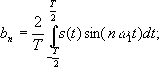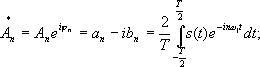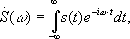Что называется спектральными характеристиками образца
Спектральные характеристики
Демидов Р.А., ФТФ, 2105
Введение
В первой части работы я поставил себе цель описать линейные операторы в целом, а также подробно рассказать о важной характеристике спектра операторов – спектральном радиусе.
В этой части работы я подробнее остановлюсь на не менее важной характеристике спектров – резольвенте, и расскажу о связи этой характеристики с подвидами спектра оператора – с остаточным, точечным и непрерывными его частями. Вначале, опять же, необходимо остановиться на некоторых основных определениях и понятиях теории линейных операторов. Итак:
— Квадратную матрицу n×n можно рассматривать как линейный оператор в n-мерном пространстве, что позволяет перенести на матрицы «операторные» термины. В таком случае говорят о спектре матрицы.
— Максимум модулей точек спектра оператора A называется спектральным радиусом этого оператора и обозначается через r(A). При этом выполняется равенство:
Это равенство может быть принято за определение спектрального радиуса,приусловии существования данного предела.
Теперь рассмотрим состав самого спектра. Он неоднороден, и состоит из следующих частей:
Таким образом, мы видим, что спектр оператора состоит из 3-х больших частей, принципиально различных.
Теорема 1: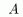 
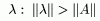
ограничен. Тогда 
является регулярной точкой.
Доказательство.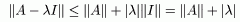 
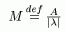
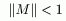
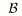
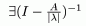
. Пусть
. Тогда 
.
— банахово, 
, причем он ограничен:
Резольвента существует и ограничена. Чтд.
Теорема 2: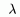 
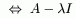
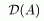
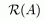
не принадлежит точечному спектру 
осуществляет биекцию 
на 
.
ð Если построена биекция, то не существует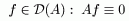 
, за исключением тривиальной.
Теорема 3: (Тождество Гильберта) 
,
,
,
верно => Чтд.
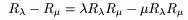
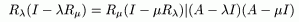
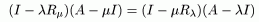
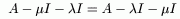
1) 
— коммутативность резольвенты.
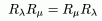
2) 
(т.к. 
непрерывна по 
в точке ), т.е. она бесконечно дифференцируема (аналитическая функция).
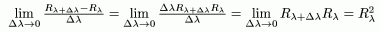
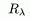
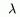
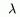
Итак,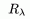 
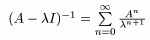
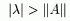
— аналитическая оператор-функция на множестве регулярных точек (резольвентном множестве). 
— разложение в ряд Лорана (имеет место при 
, но, возможно, и в большей области).
Упражнение: (Примеры вычисления спектрального радиуса)
,
.
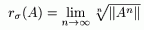
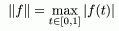
Возьмем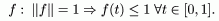
.Тогда
Таким образом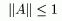 
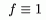
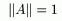
. Эта оценка достижима при 
, т.е. 
,и rc(A)=1.
Теорема 4: всякая к.ч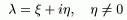 
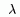
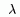
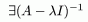
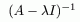
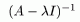
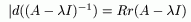
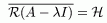
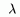
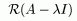
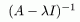
, есть регулярная точка самосопряженного оператора A.
] 
регулярная точка, значит не собственное значение и 
. Проверим ограниченность 
.
ограничен, 
и его можно распространить на 
с сохранением нормы оператора, так как 
не собственое значение. Если при этом 
не замкнуто, то 
не замкнут. При этом линейный оператор, обратный к замкнутому, а также сопряженный к нему, замкнут => самосопряженный оператор замкнут.
Спектральная теория в электронике
Полезнейшим приложением спектральной теории в физике является теория спектров электрических сигналов. Суть теории состоит в том, что любой сигнал на входе линейной цепи возможно представить совокупностью гармонических колебаний, или тестовых сигналов, заданной частоты, вопрос такого разложения состоит в нахождении амплитуд результирующих колебаний. Последние вычисляются определенным образом.
Классическое преобразование Фурье представляет из себя линейный оператор.
Спектральная теория здесь работает следующим образом – для периодических входных сигналов для нахождения соответствующих амплитуд используется интегральное преобразование – дискретный Фурье- образ:
в котором разложение начинается с частоты следования wк. В данном случае очевидно, что, раз выходной сигнал представляется суммой бесконечного ряда, то мы имеем дело с точечным спектром сигнала, поскольку он дискретен. Следовательно, любое периодическое колебание можно рассматривать как сигнал с дискретным спектром, поскольку непрерывным спектром он не обладает. Однако, если же взять непериодический сигнал, например, единичный прямоугольный импульс, то вводится понятия прямого и обратного преобразований Фурье:
,
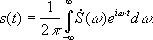
где S(w) – спектральная плотность сигнала s(t).
Соответственно, S(w) – непрерывная по w функция, и в данном.
В общем и целом, наряду с первой частью работа дает представление о б основных спектральных характеристиках линейных операторов и их применении в различных областях математики, информатики и физики.
1. Лекции по математической физике, Попов И.Ю., СПбГУ ИТМО, кафедра высшей математики.
2. Элементы теории функций и функционального анализа, А.Н. Колмогоров и С.В. Фомин.
3. Теория цепей и сигналов, Новиков Ю.Н.
4. Свободная энциклопедия Википедия.
5. Сжатие данных, изображения и звука, Д. Сэломон.
Цели и задачи курсовых, контрольных работ
Применение универсального фотометра ФМ-56 для получения спектральных характеристик поглощения твердого прозрачного образца
Применение универсального фотометра ФМ-58 для получения зависимости коэффициента отражения твердого образца от длины волны падающего света
Взаимодействие света с веществом
Формулируя законы отражения и преломления света, мы основывались только на опытных данных. Эти законы дают правильный ответ на вопрос о направлении отраженной и преломленной волн, но ничего не говорят о том, каким образом влияет на световую волну вещество тех сред, через которые проходит свет.
Распространение света в веществе представляет собой взаимодействие электромагнитного поля световой волны с электронной оболочкой атомов и молекул. Частота переменного электрического поля световой волны очень велика: около 1015Гц. Поэтому только заряженные частицы очень маленькой массы могут следовать за изменением поля световой волны. Такими частицами являются электроны. Атомы и их ядра не могут следовать за изменением этого поля в силу их большой инертной массы.
Взаимодействие электронной оболочки атомов с электромагнитным полем световой волны приводит к их возбуждению. Возбужденные атомы, приходя в нормальное (невозбужденное) состояние, излучают электромагнитные волны, получившие название вторичных волн (или вторичного излучения). Поскольку среднее расстояние между атомами в жидкостях и твердых телах мало по сравнению с длиной цуга волн (около 3м), то электронные оболочки большого числа атомов возбуждаются одним цугом волн. Поэтому вторичные волны оказываются когерентными как между собой, так и с падающей световой волной. Эти волны взаимно интерферируют. Их интерференцией объясняются явления отражения, преломления и рассеяния света в веществе.
Возможен и обратный ход дисперсии, когда показатель преломления уменьшается с уменьшением длины волны. Такой вид дисперсии называется аномальной (рис. 1 участок 2-3). Было установлено, что аномальная дисперсия тесно связана с поглощением света. Все вещества, для которых наблюдается аномальная дисперсия, сильно поглощают свет в этой области частот. На рис.1 штриховая линия изображает кривую поглощения.
Законы поглощения света
При распространении света в веществе энергия электромагнитных волн уменьшается. Это явление называется поглощением света в веществе или абсорбцией света. О поглощении света веществом принято судить по изменению его интенсивности в зависимости от пройденного расстояния.
Бугер (1729 г.) экспериментальным путем, а Ламберт (1760 г.) теоретически установили связь между интенсивностью света входящего в вещество I0 и интенсивностью света I выходящего из вещества:
где k – коэффициент поглощения, зависящий от длины волны падающего света и вида вещества, d – толщина поглощающего слоя, знак «минус» указывает на убывание интенсивности. Закон справедлив, когда падающий поток монохроматичен. Коэффициент поглощения не зависит от интенсивности света и от толщины слоя d. Из уравнения (1) следует, что коэффициент поглощения численно равен величине, обратной толщине слоя вещества, при прохождении через который интенсивность уменьшается в е = 2,72 раз.
Зависимость коэффициента поглощения от длины волны падающего света называется спектральной характеристикой вещества, определяющей окраску тел в проходящем свете. Тела, имеющие малый коэффициент поглощения в видимой области спектра, являются прозрачными неокрашенными. Например, силикатное стекло толщиной 1 см поглощает лишь около 1% проходящих через него видимых лучей. Ультрафиолетовые и далекие инфракрасные лучи это же стекло поглощает сильно. Цветными прозрачными телами называются тела, проявляющие селективность пропускания света в видимой области спектра. Так, красным является стекло, слабо поглощающее красные и оранжевые лучи, и сильно поглощающие синие, фиолетовые и зеленые.
Селективным отражением света от поверхности объясняется окраска непрозрачных тел. Синие стены хорошо отражают синий свет. Однако, окраска тела зависит не только от оптических свойств поверхности тела (красителя), но и от спектрального состава падающего света. Например, тело, покрытое красной краской, будет казаться черным при освещении его зеленым светом.
В 1862 году Беер применил закон поглощения света для определения малых количеств вещества, растворенного в прозрачном растворителе. Он показал, что для малых концентраций растворенного вещества коэффициент поглощения линейно зависит от числа молекул растворенного вещества на единицу пути света в растворе: k = k’с. Объединенное уравнение Бугера-Ламберта-Беера имеет следующий вид:
где k’– постоянная Беера, не зависящая от концентрации растворенного вещества и толщины слоя d, с– концентрация вещества. Формулу (2) можно представить и в таком виде:
где ε = k’lge – молярный коэффициент погашения.
Отношение интенсивности светового потока I, прошедшего через раствор, к интенсивности падающего светового потока I0 называется прозрачностью или пропусканием Т:
Логарифм величины, обратной пропусканию, носит название экстинкции Е или оптической плотности D:
Зависимости пропускания Т и оптической плотности D от длины волны падающего света называются спектральными характеристиками образца.
Если в растворе содержится несколько веществ, то результирующая оптическая плотность D равна сумме оптических плотностей компонент:
D = lg (I0/I) = D1+D2+… = [ε1с1 + ε2с2+…]d.
Именно поглощенное излучение представляет основной интерес для исследования, так как по закону Бугера-Ламберта-Беера оптическая плотность зависит от толщины слоя и концентрации составных частей поглощающей системы. Если свет проходит через различные поглощающие системы последовательно, то результирующая оптическая плотность D не зависит от порядка их расположения.
Условием применимости закона Беера является пропорциональность числа действующих центров поглощения концентрации растворенного вещества. В реальных растворах, наряду с молекулами поглощающего вещества, на процесс поглощения влияют своими химическими и электростатическими свойствами другие молекулы. Все эти отдельные частички соединены в один общий оптический комплекс, поэтому для концентрированных растворов с их красящими составными частями низкой степени дисперсности, закон Беера теряет свою силу.
Явление поглощения света веществом объясняется тем, что при прохождении электромагнитной волны через вещество часть энергии волны затрачивается на возбуждение колебаний оптических электронов атомов этого вещества. Частично эта энергия вновь возвращается излучению в виде вторичных волн, излучаемых атомами в возбужденном состоянии, частично же она переходит в другие виды энергии (например, во внутреннюю энергию вещества).
Так, в диэлектриках нет свободных электронов, способных направленно двигаться под действием электрического поля электромагнитной волны, и поглощение света связано с явлением резонанса при вынужденных колебаниях электронов в атомах и атомов в молекулах. Поэтому они поглощают свет избирательно в зависимости от частоты падающего света. Поглощение велико лишь в областях частот, близких к частотам собственных колебаний электронов в атомах и атомов в молекулах. Для света всех остальных частот диэлектрик практически прозрачен, то есть его коэффициент поглощения близок к нулю.
Наиболее ярко явление резонансного поглощения обнаруживается у разреженных одноатомных газов, обладающих линейчатым спектром поглощения. Дискретные частоты интенсивного (рис. 2). За пределами этих полос k примерно равен нулю, то есть диэлектрики прозрачны. Расширение полос поглощения при переходе вещества из одного агрегатного состояния в другое объясняется взаимодействием атомов друг с другом.
Иная картина наблюдается в металлах. В конденсированном состоянии металлы содержат огромное количество свободных электронов. В электрическом поле световой волны свободные электроны совершают упорядоченное движение и излучают вторичные волны. Благодаря наложению первичной и вторичной волн образуется интенсивная отраженная волна и сравнительно слабая преломленная. Преломленная волна быстро поглощается по мере распространения в металле. Ее энергия расходуется на джоулеву теплоту, которая выделяется токами проводимости, возникающими при действии света на свободные электроны.
Компьютерный чертеж
Применение универсального фотометра ФМ-56 для получения спектральных характеристик поглощения твердого прозрачного образца
Применение универсального фотометра ФМ-58 для получения зависимости коэффициента отражения твердого образца от длины волны падающего света
Взаимодействие света с веществом
Формулируя законы отражения и преломления света, мы основывались только на опытных данных. Эти законы дают правильный ответ на вопрос о направлении отраженной и преломленной волн, но ничего не говорят о том, каким образом влияет на световую волну вещество тех сред, через которые проходит свет.
Распространение света в веществе представляет собой взаимодействие электромагнитного поля световой волны с электронной оболочкой атомов и молекул. Частота переменного электрического поля световой волны очень велика: около 1015Гц. Поэтому только заряженные частицы очень маленькой массы могут следовать за изменением поля световой волны. Такими частицами являются электроны. Атомы и их ядра не могут следовать за изменением этого поля в силу их большой инертной массы.
Взаимодействие электронной оболочки атомов с электромагнитным полем световой волны приводит к их возбуждению. Возбужденные атомы, приходя в нормальное (невозбужденное) состояние, излучают электромагнитные волны, получившие название вторичных волн (или вторичного излучения). Поскольку среднее расстояние между атомами в жидкостях и твердых телах мало по сравнению с длиной цуга волн (около 3м), то электронные оболочки большого числа атомов возбуждаются одним цугом волн. Поэтому вторичные волны оказываются когерентными как между собой, так и с падающей световой волной. Эти волны взаимно интерферируют. Их интерференцией объясняются явления отражения, преломления и рассеяния света в веществе.
Возможен и обратный ход дисперсии, когда показатель преломления уменьшается с уменьшением длины волны. Такой вид дисперсии называется аномальной (рис. 1 участок 2-3). Было установлено, что аномальная дисперсия тесно связана с поглощением света. Все вещества, для которых наблюдается аномальная дисперсия, сильно поглощают свет в этой области частот. На рис.1 штриховая линия изображает кривую поглощения.
Законы поглощения света
При распространении света в веществе энергия электромагнитных волн уменьшается. Это явление называется поглощением света в веществе или абсорбцией света. О поглощении света веществом принято судить по изменению его интенсивности в зависимости от пройденного расстояния.
Бугер (1729 г.) экспериментальным путем, а Ламберт (1760 г.) теоретически установили связь между интенсивностью света входящего в вещество I0 и интенсивностью света I выходящего из вещества:
где k – коэффициент поглощения, зависящий от длины волны падающего света и вида вещества, d – толщина поглощающего слоя, знак «минус» указывает на убывание интенсивности. Закон справедлив, когда падающий поток монохроматичен. Коэффициент поглощения не зависит от интенсивности света и от толщины слоя d. Из уравнения (1) следует, что коэффициент поглощения численно равен величине, обратной толщине слоя вещества, при прохождении через который интенсивность уменьшается в е = 2,72 раз.
Зависимость коэффициента поглощения от длины волны падающего света называется спектральной характеристикой вещества, определяющей окраску тел в проходящем свете. Тела, имеющие малый коэффициент поглощения в видимой области спектра, являются прозрачными неокрашенными. Например, силикатное стекло толщиной 1 см поглощает лишь около 1% проходящих через него видимых лучей. Ультрафиолетовые и далекие инфракрасные лучи это же стекло поглощает сильно. Цветными прозрачными телами называются тела, проявляющие селективность пропускания света в видимой области спектра. Так, красным является стекло, слабо поглощающее красные и оранжевые лучи, и сильно поглощающие синие, фиолетовые и зеленые.
Селективным отражением света от поверхности объясняется окраска непрозрачных тел. Синие стены хорошо отражают синий свет. Однако, окраска тела зависит не только от оптических свойств поверхности тела (красителя), но и от спектрального состава падающего света. Например, тело, покрытое красной краской, будет казаться черным при освещении его зеленым светом.
В 1862 году Беер применил закон поглощения света для определения малых количеств вещества, растворенного в прозрачном растворителе. Он показал, что для малых концентраций растворенного вещества коэффициент поглощения линейно зависит от числа молекул растворенного вещества на единицу пути света в растворе: k = k’с. Объединенное уравнение Бугера-Ламберта-Беера имеет следующий вид:
где k’– постоянная Беера, не зависящая от концентрации растворенного вещества и толщины слоя d, с– концентрация вещества. Формулу (2) можно представить и в таком виде:
где ε = k’lge – молярный коэффициент погашения.
Отношение интенсивности светового потока I, прошедшего через раствор, к интенсивности падающего светового потока I0 называется прозрачностью или пропусканием Т:
10 –εcd.
Логарифм величины, обратной пропусканию, носит название экстинкции Е или оптической плотности D:
E = D = 
= εcd.
Зависимости пропускания Т и оптической плотности D от длины волны падающего света называются спектральными характеристиками образца.
Если в растворе содержится несколько веществ, то результирующая оптическая плотность D равна сумме оптических плотностей компонент:
D = lg (I0/I) = D1+D2+… = [ε1с1 + ε2с2+…]d.
Именно поглощенное излучение представляет основной интерес для исследования, так как по закону Бугера-Ламберта-Беера оптическая плотность зависит от толщины слоя и концентрации составных частей поглощающей системы. Если свет проходит через различные поглощающие системы последовательно, то результирующая оптическая плотность D не зависит от порядка их расположения.
Условием применимости закона Беера является пропорциональность числа действующих центров поглощения концентрации растворенного вещества. В реальных растворах, наряду с молекулами поглощающего вещества, на процесс поглощения влияют своими химическими и электростатическими свойствами другие молекулы. Все эти отдельные частички соединены в один общий оптический комплекс, поэтому для концентрированных растворов с их красящими составными частями низкой степени дисперсности, закон Беера теряет свою силу.
Явление поглощения света веществом объясняется тем, что при прохождении электромагнитной волны через вещество часть энергии волны затрачивается на возбуждение колебаний оптических электронов атомов этого вещества. Частично эта энергия вновь возвращается излучению в виде вторичных волн, излучаемых атомами в возбужденном состоянии, частично же она переходит в другие виды энергии (например, во внутреннюю энергию вещества).
Так, в диэлектриках нет свободных электронов, способных направленно двигаться под действием электрического поля электромагнитной волны, и поглощение света связано с явлением резонанса при вынужденных колебаниях электронов в атомах и атомов в молекулах. Поэтому они поглощают свет избирательно в зависимости от частоты падающего света. Поглощение велико лишь в областях частот, близких к частотам собственных колебаний электронов в атомах и атомов в молекулах. Для света всех остальных частот диэлектрик практически прозрачен, то есть его коэффициент поглощения близок к нулю.
Наиболее ярко явление резонансного поглощения обнаруживается у разреженных одноатомных газов, обладающих линейчатым спектром поглощения. Дискретные частоты интенсивного (рис. 2). За пределами этих полос k примерно равен нулю, то есть диэлектрики прозрачны. Расширение полос поглощения при переходе вещества из одного агрегатного состояния в другое объясняется взаимодействием атомов друг с другом.
Иная картина наблюдается в металлах. В конденсированном состоянии металлы содержат огромное количество свободных электронов. В электрическом поле световой волны свободные электроны совершают упорядоченное движение и излучают вторичные волны. Благодаря наложению первичной и вторичной волн образуется интенсивная отраженная волна и сравнительно слабая преломленная. Преломленная волна быстро поглощается по мере распространения в металле. Ее энергия расходуется на джоулеву теплоту, которая выделяется токами проводимости, возникающими при действии света на свободные электроны.
Лабораторная работа 311
Применение универсального фотометра ФМ-56 для получения спектральных характеристик поглощения твердого прозрачного образца
Цель работы: изучить устройство и принцип действия универсального фотометра ФМ-56, снять спектральные характеристики твердого прозрачного образца с помощью универсального фотометра ФМ-56.
Приборы и принадлежности: фотометр ФМ-56, исследуемый твердый прозрачный образец.
Принцип действия универсального фотометра ФМ-56
Универсальный фотометр предназначается для измерения пропускания (или оптической плотности) твердых и жидких прозрачных тел, измерения коэффициентов яркости светорассеивающих образцов и их блеска, а также коэффициентов отражения. Данный прибор может быть использован и в качестве сравнительного микроскопа. Фотометр ФМ-56 находит широкое применение в различных отраслях промышленности, научно-исследовательских институтах и клинических лабораториях. Действие фотометра основано на визуальном уравнивании световых потоков путем изменения одного из них с помощью диафрагмы с переменным отверстием. На рис.4 представлена оптическая схема фотометра, где 1,2 – диафрагмы, 3,4 – измерительные барабаны, 5 – ромбические призмы, 6 – объективы, 7 – окуляр, 8 – бипризма (сводит два пучка к оси окуляра).
Два световых пучка (I и II) попадают в прибор через две диафрагмы, площади которых изменяются вращением измерительных барабанов. Оптическая система прибора сводит эти пучки вместе и направляет их в глаз наблюдателя, который в своем поле зрения видит круг, разделенный линией на две половины, имеющие различную (в общем случае) яркость. Яркость левой части поля определяется световым потоком, проходящим через правую диафрагму, а яркость правой части зависит от светового потока, проходящего через левую диафрагму. Если диафрагмы 1 и 2 одинаково освещены и в одинаковой мере раскрыты, то яркости обеих половин поля зрения будут одинаковы. Если слой вещества пропускает падающий на него световой поток без заметного рассеивания, то отсчет по черной шкале барабана прибора ФМ-56 может служить мерой пропускания Т (или оптической плотности Д, если отсчет ведется по красной шкале) прозрачного образца.
Фотометр (рис.5) состоит из следующих основных узлов:
— фотометрической головки 1, в которой находятся все оптические детали (объективы, призмы и т.д.) и механизмы диафрагм;
-револьверного диска 2 со светофильтрами, которые переключаются поворотом диска (номер установленного светофильтра появляется в окошке);
— штатива, состоящего из массивного круглого основания 3 и стоек 4,5;
— предметного столика 6, который с помощью кремальерного механизма перемещается вертикально и закрепляется винтом 7 (отверстия столика центрированы относительно объективов фотометрической головки);
— плоского зеркала 8, которое может вращаться вокруг горизонтальной оси, направляя пучок света во входные отверстия фотометрической головки;
— осветителя 9 с конденсором 10 и матовыми рассеивателями 11;
— двух барабанов 12, на которые нанесены две шкалы. По одной шкале (черной ) отсчитывается пропускание, другая шкала (красная ) соответствует оптической плотности D образца.
Порядок выполнения работы
1. Включить через трансформатор 220 В лампу осветителя.
2. Вынуть матовые рассеиватели 11 (см. рис.5), установить оба барабана на деление 100, что соответствует одинаковой степени раскрытия диафрагм.
3. Ввести светофильтр №5 поворотом револьверного диска, расположенного в верхней части прибора. Затем с помощью кольца 13 сфокусировать окуляр на линию раздела полей сравнения и рассмотреть изображения спирали лампы осветителя, видимые в каждой половине поля зрения. Изображения спирали должны быть резкими (рис.6), в противном случае необходимо обратиться к преподавателю или к лаборанту. После этого матовые рассеиватели поставить на место.
4. После подготовки прибора приступить к измерению пропускания образца Т. Для этого правый барабан установить на отсчет 100 (по черной шкале). В правый пучок света поместить образец. Ввести светофильтр №1 и произвести уравнивание яркости левого и правого полей зрения и отсчет по черной и красной шкалам левого барабана. Затем вернуть левый барабан на деление 100 по черной шкале и повторить измерения еще два раза. Потом определить средние значения пропускания (Тср) и оптической плотности (Dср.) для данного светофильтра.
5. Аналогичные измерения произвести со светофильтрами № 2,3,4,5,6,7,8.
Примечание. Для тех светофильтров, при работе с которыми яркость полей сравнения очень мала или слишком велика, ручку реостата на крышке трансформатора, регулирующего накал нити лампы осветителя, можно переводить в положение «ярче» или «темнее». С очень яркими полями работать не следует.
6. Результаты измерений занести в табл.1 и построить графики. Для этого по горизонтальной оси отложить длины волн, а по вертикальной нанести измеренные значения пропускания (Тср) и оптической плотности (Dср.).