Что называется следом плоскости

Начертательная геометрия: конспект лекций.

2. Следы плоскости.

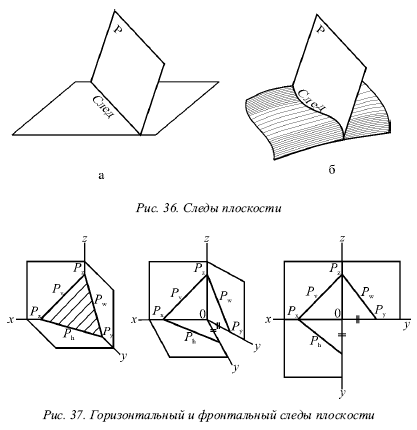
След плоскости Р – это линия пересечения ее с данной плоскостью или поверхностью (рис. 36).

Линию пересечения плоскости Р с горизонтальной плоскостью называют горизонтальным следом и обозначают Р_h, а линию пересечения с фронтальной плоскостью – фронтальным следом и обозначают Р_v (рис. 37).

Иногда применяется и профильный след Р_w – линия пересечения данной плоскости с профильной плоскостью.

Точки, в которых пересекается плоскость Р с осями проекций, называют точками схода следов. Р_х – точка схода следов на оси х, Р_у – на оси у, а Р_z – на оси z (рис. 37). в точке Р пересекаются следы Р_h и Р_v и т. д.

Следы Р_h и Р_v плоскости Р являются прямыми, которые и лежат на горизонтальной и фронтальной плоскостях. Они имеют по одной из своих проекций, которые совпадают с осью х: горизонтальный след Р_h – фронтальную, а фронтальный Р_v– горизонтальную проекции.

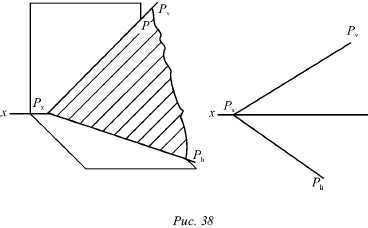
Любую плоскость Р можно задать на эпюре с помощью указания положения двух ее следов – горизонтального и фронтального (рис. 38).

Следы Р_h и Р_v чаще всего изображаются парой пересекающихся или параллельных прямых и поэтому могут определять положение плоскости в пространстве.

Источник

Научная электронная библиотека

Пиралова О. Ф., Ведякин Ф. Ф.,

2.7. Следы плоскости

Следом плоскости a называется линия пересечения этой плоскости с плоскостью проекций.

.

.

Точки пересечения плоскости a с координатными осями X, Y, Z называются точками схода следов и обозначаются соответственно S_x, S_y, S_z (рис. 2.16.а).

Вопросы для самоконтроля

1. В чем сущность построения эпюра точки?

2. Какие координаты точки однозначно определяют ее положение в пространстве?

3. Какие линии называют прямыми: а) общего; б) частного положения?

4. Какая прямая параллельна (перпендикулярна) плоскости проекций?

5. Как строят профильную проекцию точки?

6. Что называется следом прямой и как он определяется?

7. Какие плоскости являются плоскостями частного положения?

8. Что называется следом плоскости и как он определяется?

9. Как называется прямая, которая принадлежит плоскости и перпендикулярна линиям уровня этой плоскости?

Источник

Следы плоскости

След плоскости Р – это линия пересечения ее с данной плоскостью или поверхностью (рис. 36).

Линию пересечения плоскости Р с горизонтальной плоскостью называют горизонтальным следом и обозначают P_h, а линию пересечения с фронтальной плоскостью – фронтальным следом и обозначают Р_v (рис. 37).

Иногда применяется и профильный след P_w – линия пересечения данной плоскости с профильной плоскостью.

Точки, в которых пересекается плоскость Р с осями проекций, называют точками схода следов. Р_х – точка схода следов на оси х, P_у – на оси у, а Р_z – на оси z (рис. 37). в точке Р пересекаются следы P_h и P_v и т. д.

Следы P_h и P_v плоскости Р являются прямыми, которые и лежат на горизонтальной и фронтальной плоскостях. Они имеют по одной из своих проекций, которые совпадают с осью х: горизонтальный след P_h – фронтальную, а фронтальный P_v– горизонтальную проекции.

Любую плоскость Р можно задать на эпюре с помощью указания положения двух ее следов – горизонтального и фронтального (рис. 38).

Следы P_h и P_v чаще всего изображаются парой пересекающихся или параллельных прямых и поэтому могут определять положение плоскости в пространстве.

Источник

Следы плоскости

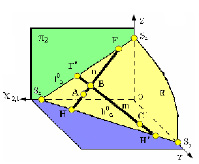
На рисунке показана плоскость общего положения α. Она пересекает плоскости проекций П₁, П₂, П₃ по прямым h_0α, f_0α и p_0α. Эти прямые называются горизонтальным, фронтальным и профильным следом плоскости α.

Оси координат пл. α пересекает в точках X_α, Y_α и Z_α. Они называются точками схода следов. При этом X_α = h_0α ∩ f_0α, Y_α = h_0α ∩ p_0α, Z_α = f_0α ∩ p_0α. Здесь знак ∩ означает пересечение.

На комплексном чертеже плоскость можно задать проекциями двух её следов. Это обеспечивает наглядность изображения и удобство при выполнении ряда построений. Стоит отметить, что угол, образованный следами плоскости на комплексном чертеже, не равен углу между ними в пространстве.

Алгоритм построения следов плоскости

На рисунке, который представлен ниже, некоторая плоскость α задана проекциями двух пересекающихся прямых a и b. Чтобы найти её следы, необходимо:

Решение задачи можно сократить. Для этого, построив горизонтальный след плоскости, фронтальный нужно провести через X_α и одну из точек, F_a или F_b. Таким образом, вместо четырех следов прямых a и b будет достаточно найти три.

Источник

Научная электронная библиотека

Пиралова О. Ф., Ведякин Ф Ф.,

2.7. Следы плоскости

Следом плоскости α называется линия пересечения этой плоскости с плоскостью проекций.

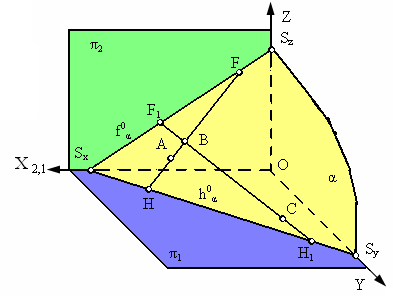
На рис. 2.19. изображена плоскость общего положения α(m∩n), образованная двумя пересекающимися прямыми, проходящими через точки А и В, расположенными в первом октанте.

Для построения следов плоскости на комплексном чертеже, необходимо помнить, что след плоскости – это линия, значит необходимо найти две точки, через которые пройдет эта линия, т. е. след плоскости. При построении плоскости за такие точки можно принять следы любых прямых линий, принадлежащих этой плоскости.

На рис. 2.19 в горизонтальной плоскости проекций π1 её горизонтальный след h0α проходит через горизонтальные следы Н и Н’ прямых m и n, а во фронтальной плоскости проекций π2 – фронтальный след плоскости f0α проходит через фронтальные следы прямых F и F’.

Рис. 2.19. Пример изображения следов плоскости α в пространстве

Для нахождения следов плоскости нужно применить правило построения следов прямых линий, который был рассмотрен выше (§2.4). Для построения горизонтального следа плоскости необходимо построить два горизонтальных следа прямых, принадлежащих плоскости, а для построения фронтального следа плоскости – два горизонтальных следа прямых, принадлежащих плоскости α(m∩n).

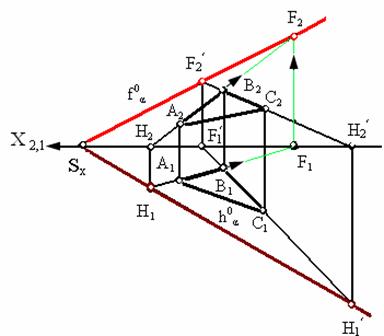
В системе двух плоскостей проекций π1 и π2 плоскость в общем случае имеет два следа: горизонтальный ha0 и фронтальный fa0, которые являются пересечением плоскости α соответственно с горизонтальной и фронтальной плоскостями проекций (рис. 2.19, 2.20).

.

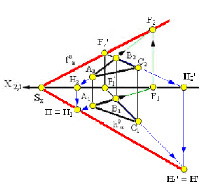
Рис. 2.20. Пример изображения следов плоскости и их алгоритм построения на комплексном чертеже

Точки пересечения плоскости α с координатными осями X, Y, Z называются точками схода следов и обозначаются соответственно Sx, Sy, Sz (рис. 2.16). На рис. 2.20. приведен комплексный чертеж плоскости треугольника АВС и разобран пример построения двух следов этой плоскости – горизонтального ha0 и фронтального fa0. Для этого выполнено построение горизонтальных следов прямых АВ и ВС, принадлежащих плоскости треугольника. Эти следы обозначены буквами Н и Н’. Решение на рисунке выполнено синими линиями со стрелками. Аналогичное построение выполнено и для фронтального следа линиями зелёного цвета. Порядок построения следов ясен из рисунка.

Вопросы для самоконтроля

1. Когда точка принадлежит какой либо плоскости проекций?

2. Как может быть задана прямая на комплексном чертеже?

3. Какие основные свойства прямой общего положения?

4. Какие частные положения относительно плоскостей проекций может занимать прямая линия?

5. Когда прямая линия может принадлежать плоскости проекций?

6. Какие прямые являются проецирующими?

7. Что называется следом прямой?

8. Как определяются на комплексном чертеже следы прямой линии?

9. Как на комплексном чертеже может быть задана плоскость?

10. Какие плоскости являются проецирующими?

11. Какие плоскости являются плоскостями уровня?

12. Какие плоскости являются плоскостями частного положения?

13. Что называется следом плоскости и как он определяется?

[1] То́чка – абстрактный объект в пространстве, не имеющий никаких измеримых характеристик (нульмерный объект).

Источник