Что называется системой счисления как они классифицируются

Системы счисления

Система счисления — это совокупность правил записи чисел посредством конечного набора символов (цифр).

Системы счисления бывают:

Непозиционные системы счисления

Примеры: унарная, римская, древнерусская и др.

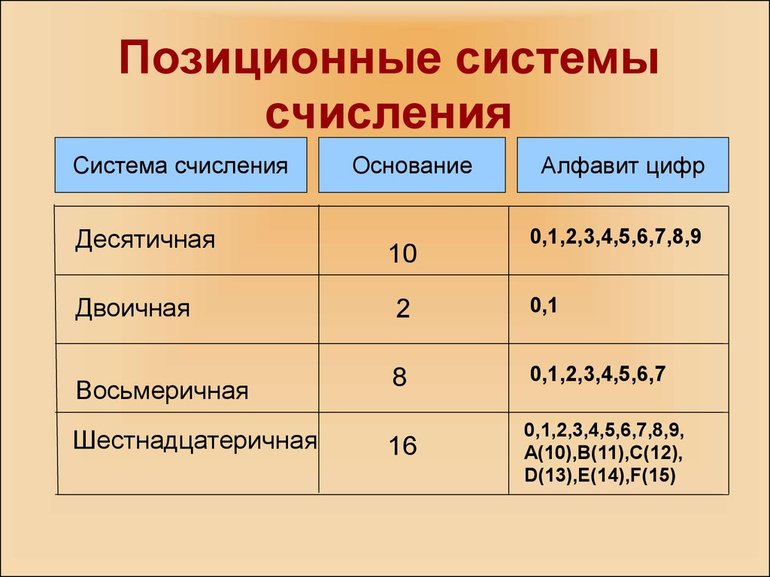
Позиционные системы счисления

Основание системы счисления —

количество различных цифр, используемых в этой системе.

отношение количественного эквивалента цифры в этом разряде к количественному эквиваленту той же цифры в нулевом разряде

где i — номер разряда, а s — основание системы счисления.

Разряды числа нумеруются справа налево, причем младший разряд целой части (стоящий перед разделителем — запятой или точкой) имеет номер ноль. Разряды дробной части имеют отрицательные номера:

По определению веса разряда

где i — номер разряда, а s — основание системы счисления.

Тогда, обозначив цифры числа как a_i, любое число, записанное в позиционной системе счисления, можем представить в виде:

Например, для системы счисления с основанием 4:

Выполнив вычисления, мы получим значение исходного числа, записанное в десятичной системе счисления (точнее, в той, в которой производим вычисления). В данном случае:

= 1⋅64 + 3⋅16 + 0⋅4 + 2⋅1 + 2⋅0,25 =

= 64 + 48 + 2 + 0,5 = 114,5

Таким образом, для перевода числа из любой системы счисления в десятичную следует:

Вспомним пример перевода из системы счисления с основанием 4 в десятичную:

1302₄ = 1⋅4 3 + 3⋅4 2 + 0⋅4 1 + 2⋅4 0 = 114

Иначе это можно записать так:

114 = ((1 ⋅ 4 + 3) ⋅ 4 + 0) ⋅ 4 + 2 = 1302₄

Отсюда видно, что при делении 114 на 4 нацело в остатке должно остаться 2 — это младшая цифра при записи в четверичной системе. Частное же будет равно

Деление его на 4 даст остаток — следующую цифру (0) и частное 1 ⋅ 4 + 3. Продолжая действия, получим аналогичным образом и оставшиеся цифры.

В общем случае для перевода целой части числа из десятичной системы счисления в систему с каким-либо другим основанием необходимо:

Источник

Общие сведения

Числа записывают при помощи определенных математических символов, значение которых зависит от системы счисления (формы представления). Последней называется метод записи числа посредством определенной совокупности знаковых элементов — цифр. Не все учащиеся понимают отличие цифры от числового значения. В учебнике по информатике для 9 класса можно встретить и такое определение: системы счисления — набор символов, используемый для обозначения цифр.

Цифра — определенный математический символ, который указывает на конкретную величину. Они составляют число, а их расположение называется разрядной сеткой.

Классификация систем счисления

В зависимости от значений символов при их расположении, системы представления значений классифицируются на 4 вида. Последние бывают:

В позиционных расположение цифры в разрядной сетке влияет на значение числа. Например, дан определенный параметр 12345. Если поменять символы местами, получится совершенно другая величина. В этом легко убедится, воспользовавшись обыкновенным калькулятором. Опыт выполняется в 2 этапа:

Результат, полученный в последнем пункте, свидетельствует, что изменение расположения цифр влияет на количественные характеристики числа.

Примером непозиционной системы счисления является обыкновенный массив данных, который строится на представлении «ключ->значение». В программировании его называют ассоциативным. Расположение его элементов не имеет значения, поскольку обращение к каждому из них осуществляется при указании соответствующего ключа.

Например, есть массив вида: login->Petr102000, password->1245ercdrg, email->petr102000@mail.ru. Чтобы узнать имя пользователя, нужно обратиться к ключу «login». Иными словами, непозиционная форма представления — набор математических символов, от положения которых не зависит результат выполнения операции.

Унарная — система счисления, элемент которой эквивалентен 1. Например, обучение счету в начальных классах при помощи палочек. Во время выполнения каких-либо работ по подсчету компонентов она также используется. Человек рисует крестик, палочку или другой символ, а затем считает их общее количество.

Смешанный тип может включать в себя все 3 системы или 2. Он применяется для подсчета денег, а основными элементами являются мелочь (монеты) и купюры.

Позиционные формы представления

Позиционные системы представления численных величин используются не только для устного счета, расчетов, но и в информационно-коммуникационных технологиях (ИКТ). Персональный компьютер переводит десятичное число в двоичную, восьмеричную и шестнадцатеричную систему (реже в троичную и пятеричную).

Основной является двоичная, поскольку из этого представления при помощи различных методик числа переводятся в другие системы исчисления. Для каждой операции существует определенный алгоритм, которого специалисты рекомендуют придерживаться.

Чтобы определить основание системы счисления, нужно внимательно рассмотреть число. Оно указывается в виде нижнего индекса или фигурными скобками. Например, А281F<16>, 0111101100<2>, 253<8>. Однако в первом случае его можно не указывать, поскольку и так понятно, что это шестнадцатеричная форма записи величины (используются элементы английского алфавита).

Двоичный код можно записывать без фигурных скобок, т. к. он отличается от восьмеричной, пятеричной и других представлений чисел. Если речь идет о восьмеричной, в фигурных скобках указывается 8.

Существует также понятие мощности систем информационного исчисления. Эта характеристика показывает, какое количество данных можно закодировать. Например, картинки кодируются при помощи набора символов шестнадцатеричной формы представления, имеющей больший по сравнению с другими параметр мощности.

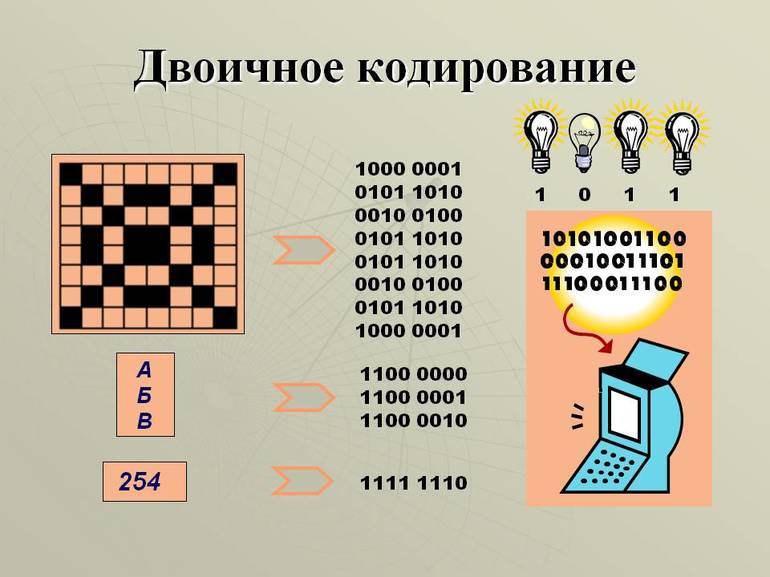
Работа с двоичным кодом

Двоичный код состоит из 0 и 1, что довольно просто реализовать в разнообразных электронных устройствах. Кодирование осуществляется наличием или отсутствием электромагнитного поля, закрытым или открытым переходом полупроводникового транзистора. В этом случае прослеживается связь информатики и вычислительной техники с физикой.

Для конвертации десятичной формы в двоичную применяются 2 способа. К ним относятся:

Новичку в сфере IT необходимо знать алгоритм конвертации двоичного кода в десятичный и обратную операцию. Методика для деления в столбик (преобразование в двоичную форму) имеет такой вид:

Обратная конвертация из двоичного кода в десятичную форму имеет немного другую методику. Суть ее состоит в следующем:

Следующий способ конвертации десятичной формы в двоичную называется степенным. Суть его в том, что нужно составлять специальную таблицу:

Таблица 1. Степень 2 и ее величина.

Методика преобразования строится по определенному алгоритму. Последний имеет такой вид:

Чтобы понять методику конвертации при помощи степенного способа, нужно разобрать ее реализацию на практическом примере:

Каждый ученик должен сам выбрать для себя оптимальный способ. Для проверки можно воспользоваться специальным калькулятором или веб-приложением для конвертации из одной системы представления величины в другую.

Восьмеричная запись

Перевод в восьмеричную форму из десятичной осуществляется через двоичный код. После чего элементы разрядной сетки группируются по триадам, а затем высчитывается результат. Чтобы привести число к восьмеричной форме, нужно использовать следующий алгоритм:

Для использования алгоритма необходимо разобрать пример преобразования числа 117 в восьмеричный код. Это делается таким образом:

Алгоритм обратного преобразования строится на конвертации сначала в двоичную, а затем в десятичную форму. Он имеет следующий вид:

Конвертация проверяется при помощи различных онлайн-сервисов или калькулятора. Восьмеричная система позиционного счисления обладает большей мощностью, чем двоичная.

Шестнадцатеричный формат

Для выполнения перевода десятичного числа в шестнадцатеричное (ее также можно назвать HEX-представление) существует определенная методика, похожая на предыдущую (восьмеричную), но имеющая некоторые отличия. Последние заключаются в выделении тетрад (4 элемента), а также расширения количества математических символов (от 0 до 9, А = 10, В = 11, С = 12, D = 13, Е = 14 и F = 15). Алгоритм имеет следующий вид:

Для полного понимания методики конвертации нужно разобрать практический пример. Реализация алгоритма выглядит следующим образом:

Обратная методика преобразования строится на переводе в двоичную форму, а затем в десятичную. Она имеет такой вид:

Во втором пункте специалисты рекомендуют указывать основание, т. к. этот прием поможет избежать ошибок при конвертации. Кроме того, результат необходимо проверять при помощи веб-сервиса или специального калькулятора.

Таким образом, системы счисления используются для конвертации цифровой информации в машинный код для дальнейшей обработки и выдачи готовых результатов, полученных во время вычислительного процесса.

Источник

Системы счисления в математике

Содержание:

Системы счисления в математике

Система счисления — это совокупность правил записи чисел посредством конечного набора символов (цифр). Системы счисления бывают: непозиционными (в этих системах значение цифры не зависит от ее позиции — положения в записи числа).

Непозиционные системы счисления

Непозиционными называются такие системы счисления, в которых каждая цифра сохраняет своё постоянное значение независимо от того места, которое она занимает в записи числа.

Примером непозиционной системы счисления, которая дошла до наших дней и иногда используется, является римская система счисления. В этой системе для записи чисел используется такие цифры: I, V, X, C, D, M и т.д., они обозначают числа один, пять, десять, пятьдесят, сто, тысяча и т.д. Запись любых других чисел производится на основе определённых правил: несколько одинаковых цифр, стоящих рядом, отображают число, равное сумме чисел, которые соответствуют этим цифрам, например III — три, XX — двадцать, пара цифр в которой младшая цифра (которая обозначает меньшее число) стоит слева от старшей (которая обозначает большее число), отображает разность соответствующих чисел, например IV — четыре, XL — сорок, пара цифр, в которой младшая цифра стоит справа от старшей, отображает сумму соответствующих чисел, например XI — одиннадцать, VI — шесть, и т.п.

Позиционные системы счисления

Позиционными называются такие системы счисления, в которых значение каждой цифры определяется не только самой цифрой, но и тем местом (позицией), которое она занимает в записи числа.

Основой позиционной системы счисления называется число , которое показывает, сколько необходимо единиц любого разряда для получения единицы старшего разряда. Систему счисления с основой будем обозначать через . Очевидно, что основой системы счисления определяется количество цифр, которые используются для записи чисел в данной системе счисления. Основой десятичной системы счисления является число десять, для записи любых чисел используется только десять разных чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

В позиционной системе счисления с основой используются разных целых чисел , которые называются базой системы счисления. Различаются позиционные системы счисления с неотъемлемой и симметричной базой. В позиционных системах счисления с неотъемлемой базой цифры означают последовательные целые числа начиная с нуля; в позиционных системах счисления с симметричной базой цифры обозначают последовательные целые числа, симметрично расположенные относительно нуля и ноль. Как правило, цифры 0, 1 в позиционных системах счисления обозначают число ноль и единицу.

Числа в позиционной системе счисления с основой записывают как последовательность цифр системы , разделённых запятой на целую и дробную части. Если буквы обозначают цифры системы, то последовательность цифр означает число .

Арифметические действия над числами в любой позиции системы счисления выполняются по тем же правилам, что и в десятичной системе. Однако, при выполнении действий над числами системы, необходимо пользоваться таблицами сложения и умножения этой системы.

Чтобы различать в какой системе счисления записано то или другое число, договоримся обозначать через число х, записанное в системе счисления .

Рассмотрим наиболее внедрённые в ЭВМ системы счисления.

Двоичная система счисления

Эта система счисления использует две цифры 0, 1, которые обозначают числа ноль и единицу соответственно. Основой этой системы является число два.

Ниже дано изображения некоторых чисел в двоичной системе счисления:

При добавлении двух чисел, записанных в двоичной системе счисления, следует пользоваться таблицей сложения:

Таблица умножения в двоичной системе счисления также очень простая:

Примеры

Восьмеричная система счисления

Эта система счисления использует цифры 0, 1, 2, 3, 4, 5, 6, 7 для обозначения последовательных чисел от нуля до семи включительно. Основой этой системы является число 8. Запись произвольного числа в этой системе основывается на его разложении по степеням числа восемь с указанными выше коэффициентами.

Запишем некоторые числа в восьмеричной системе счисления:

Восьмеричные таблицы сложения и умножения имеют вид:

Примеры

Шестнадцатеричная система счисления

Эта система счисления использует шестнадцать цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, которые обозначают последовательно целые числа, начиная с нуля заканчивая числом «пятнадцать». Основой этой системы счисления является число шестнадцать.

Запишем некоторые числа в шестнадцатеричной системе счисления:

Примеры

Переведение чисел из одной системы в другую

При решении задач на ЭВМ начальные данные, как правило, задаются в десятичной системе счисления, в той же системе необходимо получить результат. Однако почти все машины работают не в десятичной системе, а в какой-нибудь другой, например в двоичной. Поэтому возникает необходимость переведения чисел из одной системы в другую. При рассмотрении правил перевода чисел из одной системы счисления в другую ограничимся только системами счисления с неотъемлемой базой. Поскольку переведение отрицательных чисел сводится к переводу абсолютных величин и приписыванием им знака минус, то достаточно рассмотреть перевод положительных чисел.

Перевод чисел системы в систему с помощью арифметики системы .

Такой перевод будем обозначать символами .

Для того, чтобы число , записанное в системе .

перевести в систему , пользуясь арифметикой системы , необходимо:

а) записать число в виде:

б) заменить основу 10 и все цифры системы их изображениями в системе ;

в) сделать вычисления, пользуясь арифметикой системы .

Примеры:

Проведя вычисления, пользуясь арифметикой десятичной системы счисления, получаем число 22,75₁₀.

б) Перевести число 27,5₁₀ из десятичной системы счисления в двоичную

то, заменив основу 10 и цифры 2, 7, 5 их изображением в двоичной системе счисления, получаем:

Сделав вычисления, пользуясь арифметикой двоичной системы счисления, получим число .

Следовательно,

в) Перевести число 634,52₈ из восьмеричной системы счисления в десятичную (8 → 10(10)).

Подав это число в виде

и заменив основу 10 — числом 8 (цифры 6, 3, 4, 5, 2 имеют тот же вид в десятичной системе счисления) получаем:

Сделав вычисления, пользуясь арифметикой десятичной системы счисления, получаем число 412,93750₁₀.

Следовательно, 634,52_{8 =} 412,93750_10.

г) Перевести число 98,6₁₀ из десятичной системы счисления в восьмеричную (10 →8(8)).

Представив это число в виде

и заменив основу числа 10 и цифры 9, 8, 6 их видом в восьмеричной системе счисления, получим:

Сделав вычисления, руководствуясь арифметикой восьмеричной системы счисления получим число 142,4₈. Следовательно, 98,6₁₀ = 142,4₈.

Перевод чисел системы в систему с помощью арифметики системы

Перевод чисел системы в систему с помощью арифметики системы .

Такой перевод будем обозначать символами . Поскольку для перевода любого числа достаточно уметь переводить его дробную и целую части, то можно рассмотреть эти оба случая отдельно.

Перевод целых чисел

Пусть целое число , записанное в системе , необходимо перевести в систему . Поскольку — целое число, то его вид в системе будет таким:

где цифры системы , которые необходимо определить, а 10 — основа системы .

Заменим цифры и основу 10 системы их видом в системе . Пусть является изображением цифры изображением основы системы в системе .

Разделив обе части полученного равенства на , получим остаток и частное

Если теперь частное разделить на , то получим остаток и частное

Повторяя этот процесс раз, мы последовательно найдём все числа , причём последнее частное Деление выполняем, пользуясь арифметикой системы .

Таким образом, при последовательном делении числа и частных, которые получаем при делении, на основу системы, записанную в системе, то есть на , получим в виде остатков от деления цифры, необходимое для изображения числа в системе , записанные в системе . Последовательное деление производится до тех пор, пока не одержим частное, меньше чем . Это последнее частное даст нам цифру числа , записанную в системе. При делении пользуются арифметикой системы .

Примеры

а) Перевести число 65₁₀ из десятичной системы счисления в двоичную (10 → 2(10)).

и десятичные цифры 0, 1 имеют тоже самое изображение в двоичной системе счисления, то 65₁₀ = 1000001₂

б) Перевести число 325₁₀ из десятичной системы счисления в восьмеричную (10 → 8(10)).

и десятичные цифры 5, 0 имеют тоже самое изображение в восьмеричной системе счисления, то 325₁₀ = 505₈.

в) Перевести число 3060₁₀ из десятичной системы в шестнадцатеричную (10→16(10)).

а десятичные цифры 15, 11 изображаются в шестнадцатеричной системе счисления как F и B, 3060₁₀ = BF4₁₆.

г) Перевести число 111011₂ из двоичной системы счисления в десятичную (2→10(2)).

Пользуясь арифметикой двоичной системы счисления, получим:

Двоичные числа 101 и 1001 в десятичной системе счисления имеют изображение 5 и 9 соответственно, 111011₂ = 59₁₀.

Переведение правильных дробей

Пусть D — правильная дробь, записанная в системе P. Допустим, что необходимо перевести дробь в систему . Пусть изображение D в системе найдём и она имеет изображение

Умножим две части полученного равенства на . Получим число, целая часть которого и дробная часть

Умножим на , получим число, целая часть которого и дробная

Повторяя умножение необходимое нам количество раз, мы найдём одну за одной цифры, необходимые нам для изображения числа D в системе . При умножении пользуемся арифметикой системы P.

Таким образом, при последовательном умножении числа D и дробных частей произведения, которые получаются при умножении на основу , записанную в системе P, то есть на , получим в виде целых частей произведений цифры, необходимые для изображения числа D в системе . Умножение выполняем, пользуясь арифметикой системы P.

Примеры:

а) Перевести число 0,5625₁₀ из десятичной системы исчисления в восьмеричную (10→8(10)).

и десятичная цифра 4 имеет то же самое изображение в восьмеричной системе счисления, то 0,5625₁₀ = 0,44₈.

б) Перевести число 0,375₁₀ из десятичной системы исчисления в двоичную (10→2(10)).

и десятичные цифры 0, 1 имеют то же самое изображение в двоичной системе счисления, то 0,375₁₀ = 0,0012.

в) Перевести число 0,5B4₁₆ из шестнадцатеричной системы исчисления в десятичную (16→10(16)).

и шестнадцатеричные цифры 5, 5, 5, 6, 0, 1, 2 имеют то же самое изображение в десятичной системе счисления, то 0,5B4₁₆ = 0,3569015625₁₀.

Замечание: Удобнее всего, при переводе чисел из системы счисления P в систему , пользоваться арифметикой системы P, если

Перевод чисел системы в систему и наоборот, если .

Пусть , где целые положительные числа. В этом случае общие правила перевода значительно упрощаются.

Для того, чтобы перевести число системы в систему при , достаточно каждую цифру этого числа заменить соответствующим -разрядным числом в системе .

Для того, чтобы перевести число системы в систему при , достаточно, двигаясь от запятой влево и вправо, разбить все цифры числа на группы по цифр в каждой (крайние группы дополняются нулями, если это необходимо) и каждую группу заменить соответствующей цифрой системы .

Примеры:

Трёхразрядное двоичное число, которое соответствует определённой восьмеричной цифре, называется триадой. Соответствие между восьмеричными цифрами и триадами такое:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник