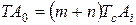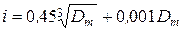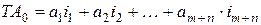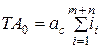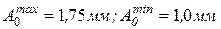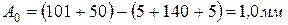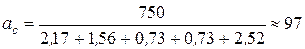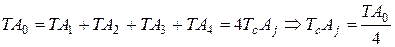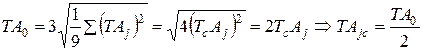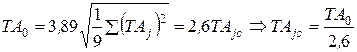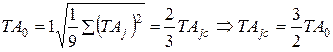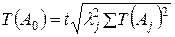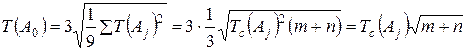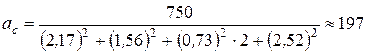Что называется размерной цепью

Размерные цепи. Понятия и определения. Методы решения

Размерной цепью называется совокупность взаимосвязанных разме­ров, определяющих взаимное расположение осей и поверхностей одной детали или нескольких деталей в изде­лии, расположенных в определённой последовательности по замкнутому контуру и непосредственно влияющих на точность одного из размеров контура.

Каждая размерная цепь состоит из составляющих звеньев (размеров) цепи и замыкающего звена (размера).

Замыкающим размером называется размер, получаю­щийся последним в процессе обработки детали или сборки узла, величина и точность которого зависят от величины и точности всех остальных раз­меров цепи, называемых составляющими. По взаимному расположению размеров размерные цепи делятся на линейные, плоскостные и пространственные.

Линейными называются размерные цепи, звенья которых располо­жены параллельно друг другу.

Плоскостными называются размерные цепи, все или часть звеньев которых не параллельны друг другу, но расположены в одной или не­скольких параллельных плоскостях.

Пространственными называются размерные цепи, все или часть звеньев которых не параллельны друг другу и расположены в непарал­лельных плоскостях

Увеличивающими называются составляющие размеры, при увеличе­нии которых замыкающий размер увеличивается.

Уменьшающими называются составляющие размеры, при увеличе­нии которых замыкающий размер уменьшается.

Размер сборочной размерной цепи, который определяет функциони­рование узла или механизма, называется исходным (функциональным) раз­мером (зазор, натяг, величина перемещения детали и т. д.). В процессе сборки этот размер, как правило, является замыкающим.

Предельные отклонения размеров назначают, в основном, руково­дствуясь следующими правилами:

— допуск назначается в тело детали;

— для охватывающих размеров отклонение назначается в «+»;

— для охватываемых размеров отклонение назначается в «-» ;

При расчете размерных цепей различают прямую и обратную задачи.

Прямая задача заключается в определении допуска и предельных от­клонений составляющих размеров по заданным номинальным размерам всех звеньев цепи и заданным предельным отклонениям исходного (замы­кающего) звена.

Обратная задача заключается в определении номинального значе­ния, допуска и предельных отклонений замыкающего размера по задан­ным номинальным размерам и предельным отклонениям составляющих звеньев.

Прямая задача, связанная с размерными цепями, решается при проектировании новых конструкций деталей, узлов и машин (проектные расчеты).

Обратная задача решается в случаях, когда в чертежах допуски на составляющие размеры установлены конструктором, исходя из конструктивных, технологических и экономических соображений и требуется проверить их соответствие допуску замыкающего звена (проверочные расче­ты).

Как прямые, так и обратные задачи размерного анализа можно решать методом полной взаимозаменяемости; теоретико-вероятностным методом и другими методами, обеспечивающими неполную взаимозаменяемость.

Плоские и пространственные размерные цепи рассчитывают те­ми же методами, что и линейные. Необходимо лишь привести их к виду линейных размерных цепей. Это достигается путем проек­тирования размеров плоской цепи на одно направление, обычно совпадающее с направлением замыкающего размера, а пространст­венной цепи — на две или три взаимно перпендикулярные оси.

В размерном анализе и синтезе конструкций машин выбирают методы-достижения точности замыкающего звена, обусловленные способами решения размерных цепей. Методы и способы автоном­ны и к ним относятся следующие.

Метод полной взаимозаменяемости — метод, при кото­ром требуемая точность замыкающего звена размерной цепи до­стигается во всех случаях ее реализации путем включения составля­ющих звеньев без выбора, подбора или изменения их значений. Чтобы обеспечить полную взаимозаменяемость, размерные цепи рассчитывают способом на максимум-минимум, учитывающим только предельные отклонения звеньев размерной цепи и самые неблагоприятные их сочетания при помощи системы аддитивных допусков. При таких допусках влияние их на издержки производст­ва значительное. Обеспечение заданных предельных отклонений при этом приводит к резкому повышению стоимости, а поэтому рас­четы экономически оптимальной точности необходимы.

Метод неполной взаимозаменяемости применяется, когда требуемая точность замыкающего звена размерной цепи достигает­ся с некоторым риском путем включения в нее составляющих звеньев без участия других методов. В этом случае допускаются перекрывающиеся допуски, и сборка может проходить с помощью методов групповой взаимозаменяемости, регулирования, пригонки, опираясь на теоретико-вероятностный метод расчета. Теорети­ко-вероятностный метод ограничивает выпуск бракованной про­дукции до небольшого допустимого предела с применением систе­мы перекрывающихся допусков на основе случайного отбора де­талей.

При методе групповой взаимозаменяемости требуемая точность замыкающего звена размерной цепи достигается путем включения в размерную цепь составляющих звеньев, принадлежа­щих к соответственным группам, на которые они предварительно рассортированы. Выбор метода представляет экономическую про­блему и предполагает дополнительные издержки производства. Сортировка деталей увеличивает затраты на новую измерительную технику и привлекает дорогостоящие контрольные автоматы. Уве­личиваются затраты труда контролеров. Растут складские расходы в связи с дополнительными затратами по хранению отсортирован­ных деталей.

В методе регулирования требуемая точность замыкающе­го звена размерной цепи достигается изменением значения ком­пенсирующего звена без удаления материала с компенсатора. Роль компенсатора обычно выполняет специальное звено в виде прок­ладки, регулируемого упора, клина и т. д. При этом по всем остальным размерам цепи детали обрабатывают по расширенным допускам, экономически приемлемым для данных производствен­ных условий. К недостаткам метода следует отнести увеличение числа деталей в машине, что усложняет конструкцию, сборку и экс­плуатацию.

В методе пригонки требуемая точность замыкающего звена размерной цепи достигается изменением значения компенсирующе­го звена путем удаления с компенсатора определенного слоя мате­риала по оставленному припуску. Применяют способы совместной обработки деталей и при большом объеме выполняемых работ, при высокой точности его автоматизируют.

Задача синтеза (прямая) — та, при которой заданы парамет­ры замыкающего звена (номинальное значение, допустимые от­клонения и допуски) и требуется определить параметры составля­ющих звеньев.

Задача анализа (обратная) — задача, в которой известны параметры составляющих звеньев и требуется определить парамет­ры замыкающего звена.

С учетом факторов, влияющих на изменение звеньев размерной цепи во времени, решаются две задачи — статическая и динамичес­кая.

Сущность расчета размерной цепи заключается в установлении допусков, предельных отклонений, координат их середин, номи­нальных размеров всех звеньев.

По виду задач, в решении которых участвуют цепи, они делятся на конструкторские, технологиче­ские и измерительные.

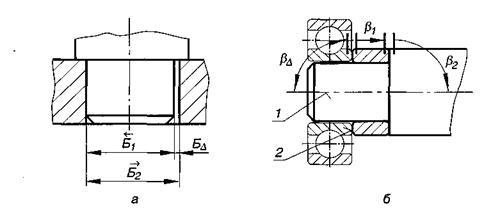
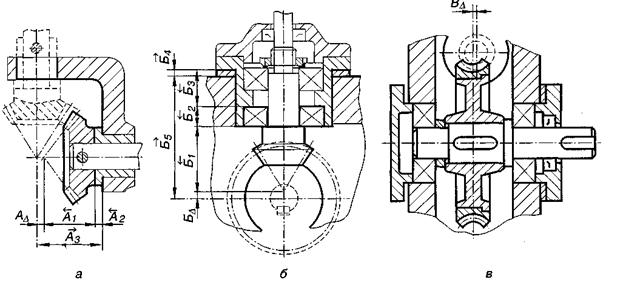
Конструкторские размерные цепи решают задачу по обеспечению точности при конструирова­нии. Они устанавливают связь размеров детали в изделии. На рис. 9.1 приведены примеры сбо­рочных размерных цепей.

На рис. 9.1, а приведена элементарная сборочная размерная цепь, решающая задачу обеспе­чения точности сопряжения двух деталей. На рис 9.1, б тоже показана сборочная цепь, которая решает задачу обеспечения перпендикулярности поверхности 2 к оси 1, необходимой для базиро­вания подшипника качения.

Рис. 9.1 Примеры сбо­рочных размерных цепей.

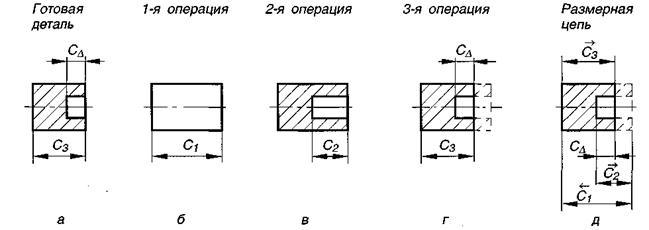
Технологические размерные цепи решают задачу по обеспечению точности при изготовлена машин. Они устанавливают связь размеров деталей на разных этапах технологического процесса. На рис. 9.2, а изображена деталь с размерами, которые следует выдержать при изготовлении. По­следовательность получения размеров приведена на рис. 9.2, б, в, г. На основании предложенного маршрута обработки построена технологическая размерная цепь (см. рис 9.2, д). При обработке детали выдерживаются размеры С₁, С₂, С_з, а размер С_Δ получается автоматически.

Рис. 9.2. Принципы построения конструкторских размерных цепей

Перед тем как построить размерную цепь, следует выявить замыкающее звено, которое, допустим, определяет нормальное функционирование механизма. Размер или предельное отклонение замы­кающего звена назначают или рассчитывают исходя из условий работы и/или требуемой точности.

Например, размер и предельные отклонения замыкающего звена А_Δ принимаются такими, которые обеспечивали бы свободное вращение зубчатого колеса при минимальном возможном смещении его вдоль оси. Несовпадение вершины делительного конуса конической шестерни с осью вращения конического колеса (рис. 9.5, а, б) определяется степенью точности зубчатых колес, а его предель­ные значения находятся по соответствующему стандарту. Надо только установить, между какими деталями стоит размер замыкающего звена, а затем связать эти детали цепью раз­меров.

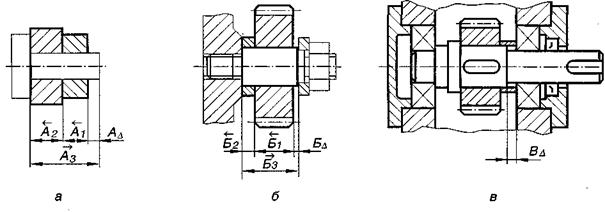
Например, на рис. 9.3, б размер замыкающего звена Б_Δ стоит между осью и торцом зубчатого колеса; на рис. 9.5, a A_Δ стоит между осью отверстия в корпусе и вершиной делительного конуса конического колеса и т. Д.

Рассмотрим наиболее типичные варианты сборочных размерных цепей*. Первый вид размер­ных цепей приведен на рис. 9.3, второй — на рис. 9.4., третий — на рис. 9.5.

Рис. 9.3. Первый вид размерной цепи.

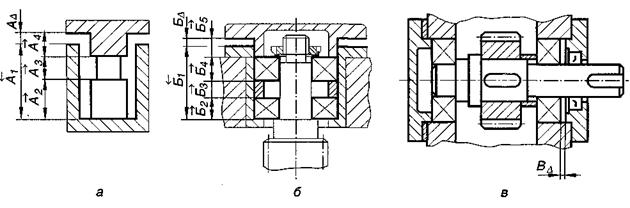
Рис. 9.4. Второй вид размерной цепи.

Рис. 9.4. Третий вид размерной цепи.

При построении размерных цепей следует руководствоваться их основными свойствами:

— цепь должна быть замкнута;

— размер любого звена сборочной цепи должен относиться к элементам одной и той же дета­ли; исключением является замыкающее звено, которое всегда соединяет элементы разных деталей;

— цепь должна быть проведена наикратчайшим способом, т. е. деталь своими элементами должна входить в размерную цепь только один раз.

Основные соотношения размерных цепей

Размерная цепь всегда замкнута. На основании этого свойства существует зависимость, которая связывает номинальные размеры звеньев.

Для плоских размерных цепей с номинальными звенья ми она имеет следующий вид:

(9,1)

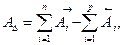
где: n и p — число соответственно увеличивающих и уменьшающих звеньев в размерной цепи. Для определения зависимости, которая связывает допуски звеньев в размерной цепи, найдем вначале наибольшее значение замыкающего звена:

(9.2)

затем наименьшее значение:

(9.3)

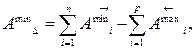
Вычитая из (9.2) (9.3) получаем:

(9.4)

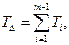
где: m – количество звеньев размерной цепи, включая замыкающее звено.

Методы решения размерных цепей

Метод полной взаимозаменяемости. Метод, при котором требуемая точность замыкающего звена размерной цепи получается при лю­бом сочетании размеров составляющих звеньев. При этом предполагают, что в размерной цепи одновременно могут оказаться все звенья с предельными значениями, причем в любом из двух наиболее неблагоприятных сочетаний (все увеличивающие звенья с верхними предельными разме­рами, а уменьшающие с нижними, или наоборот). Такой метод расчета, который учитывает эти не­благоприятные сочетания, называется методом расчета на максимум — минимум.

Метод неполной взаимозаменяемости. Это метод, при котором требуемая точность замыкающего звена размерной цепи получается не при любых сочетаниях, а при ранее обусловленной части сочетаний размеров составляющих звеньев.

Сборка осуществляется без пригонки, регулировки и подбора звеньев.

Метод исходит из предположения, что сочетание действительных размеров составляющих звеньев в изделии носит случайный характер, и вероятность того, что все звенья с самыми небла­гоприятными сочетаниями окажутся в одном изделии, весьма мала.

Такой метод расчета, который учитывает рассеяние размеров и вероятность их различных со­четаний, называется вероятностным методом расчета. Другими словами, метод допускает малый процент изделий, у которых замыкающее звено выйдет за рамки поля допусков. При этом расши­ряются допуски составляющих цепь размеров, и тем самым снижается себестоимость изготовле­ния деталей.

Задачей расчета является назначение допусков на составляющие звенья, соответствующих оди­наковой степени точности.

Метод пригонки. Это метод, при котором требуемая точность замыкающего звена размерной цепи достигается из­менением размера компенсирующего звена путем снятия с компенсатора слоя металла. Его суть состоит в том, что допуски на составляющие звенья назначаются по экономически приемлемым квалитетам, например по 12-14-му квалитетам. Получающийся после этого у замыкающего звена избыток поля рассеяния при сборке устраняют за счет компенсатора.

Метод регулирования с применением неподвижного компенсатора

Это метод, при котором требуемая точность замыкающего звена размерной цепи достигается из­менением компенсирующего звена без снятия слоя металла.

Его суть состоит в том, что избыток поля рассеивания замыкающего звена устраняют путем подбора компенсатора из некоторого количества компенсаторов, заранее изготовленных с различ­ными размерами.

Смысл расчета заключается в определении наименьшего количества компенсаторов в комплекте.

Смысл расчета заключается в определении припуска на пригонку, достаточного для компенса­ции величины превышения предельных значений замыкающего звена и вместе с тем наименьшего для сокращения объема пригоночных работ.

Роль компенсатора обычно выполняет деталь, наиболее доступная при разборке механизма, несложная по конструкции и неточная, например прокладки, шайбы проставочные.

Источник

Основные понятия о размерных цепях

Размерной цепью называется совокупность взаимосвязанных разме­ров, определяющих взаимное расположение осей и поверхностей одной детали или нескольких деталей в изде­лии, расположенных в определённой последовательности по замкнутому контуру и непосредственно влияющих на точность одного из размеров контура.

Каждая размерная цепь состоит из составляющих звеньев (размеров) цепи и замыкающего звена (размера).

Замыкающим размером называется размер, получаю­щийся последним в процессе обработки детали или сборки узла, величина и точность которого зависят от величины и точности всех остальных раз­меров цепи, называемых составляющими. По взаимному расположению размеров размерные цепи делятся на линейные, плоскостные и пространственные.

Линейными называются размерные цепи, звенья которых располо­жены параллельно друг другу.

Плоскостными называются размерные цепи, все или часть звеньев которых не параллельны друг другу, но расположены в одной или не­скольких параллельных плоскостях.

Пространственными называются размерные цепи, все или часть звеньев которых не параллельны друг другу и расположены в непарал­лельных плоскостях

Увеличивающими называются составляющие размеры, при увеличе­нии которых замыкающий размер увеличивается.

Уменьшающими называются составляющие размеры, при увеличе­нии которых замыкающий размер уменьшается.

Размер сборочной размерной цепи, который определяет функциони­рование узла или механизма, называется исходным (функциональным) раз­мером (зазор, натяг, величина перемещения детали и т. д.). В процессе сборки этот размер, как правило, является замыкающим.

Предельные отклонения размеров назначают, в основном, руково­дствуясь следующими правилами:

— допуск назначается в тело детали;

— для охватывающих размеров отклонение назначается в «+»;

— для охватываемых размеров отклонение назначается в «-» ;

При расчете размерных цепей различают прямую и обратную задачи.

Прямая задача заключается в определении допуска и предельных от­клонений составляющих размеров по заданным номинальным размерам всех звеньев цепи и заданным предельным отклонениям исходного (замы­кающего) звена.

Обратная задача заключается в определении номинального значе­ния, допуска и предельных отклонений замыкающего размера по задан­ным номинальным размерам и предельным отклонениям составляющих звеньев.

Прямая задача, связанная с размерными цепями, решается при проектировании новых конструкций деталей, узлов и машин (проектные расчеты).

Обратная задача решается в случаях, когда в чертежах допуски на составляющие размеры установлены конструктором, исходя из конструктивных, технологических и экономических соображений и требуется проверить их соответствие допуску замыкающего звена (проверочные расче­ты).

Как прямые, так и обратные задачи размерного анализа можно решать методом полной взаимозаменяемости; теоретико-вероятностным методом и другими методами, обеспечивающими неполную взаимозаменяемость.

Плоские и пространственные размерные цепи рассчитывают те­ми же методами, что и линейные. Необходимо лишь привести их к виду линейных размерных цепей. Это достигается путем проек­тирования размеров плоской цепи на одно направление, обычно совпадающее с направлением замыкающего размера, а пространст­венной цепи — на две или три взаимно перпендикулярные оси.

В размерном анализе и синтезе конструкций машин выбирают методы-достижения точности замыкающего звена, обусловленные способами решения размерных цепей. Методы и способы автоном­ны и к ним относятся следующие.

Метод полной взаимозаменяемости — метод, при кото­ром требуемая точность замыкающего звена размерной цепи до­стигается во всех случаях ее реализации путем включения составля­ющих звеньев без выбора, подбора или изменения их значений. Чтобы обеспечить полную взаимозаменяемость, размерные цепи рассчитывают способом на максимум-минимум, учитывающим только предельные отклонения звеньев размерной цепи и самые неблагоприятные их сочетания при помощи системы аддитивных допусков. При таких допусках влияние их на издержки производст­ва значительное. Обеспечение заданных предельных отклонений при этом приводит к резкому повышению стоимости, а поэтому рас­четы экономически оптимальной точности необходимы.

Источник

Лекция № 8 «Размерные цепи»

Основные термины и определения теории размерных цепей. (ГОСТ 16319-80)

Для нормальной работы любого механизма необходимо, чтобы составляющие его детали и их поверхности занимали друг относительно друга определенное положение, соответствующее их служебному назначению.

При расчете точности взаимного расположения деталей и их поверхностей учитывают взаимосвязь многих размеров. Эту взаимосвязь устанавливают с помощью размерных цепей.

Размерной цепью называют совокупность геометрических размеров, расположенных по замкнутому контуру и определяющих взаимное расположение деталей и их поверхностей.

Звеньями размерной цепи называются размеры, составляющие размерную цепь.

Классификация размерных цепей.

По области применения:

а) конструкторская – решается задача обеспечения точности при конструировании изделий.

б) технологическая – решается задача обеспечения точности при изготовлении изделий.

в) измерительная – решается задача измерения величин, характеризующих точность изделий.

По месту в изделии:

а) детальная – определяет точность относительного положения поверхностей или осей одной детали.

б) сборочная – определяет точность относительного положения поверхностей или осей деталей, входящих в сборочную единицу.

По расположению звеньев:

а) линейная – звенья цепи являются линейными размерами и расположены на параллельных прямых.

б) угловая – звенья цепи представляют собой угловые размеры.

в) плоская – звенья расположены произвольно в одной или нескольких параллельных плоскостях.

г) пространственная – звенья расположены произвольно в пространстве.

Любая размерная цепь имеет одно исходное (замыкающее) звено и два или более составляющих звеньев.

Исходным называют звено, которое определяет функционирование механизма. Размер этого звена указывают в специальных технических требованиях на сборочных чертежах. Это понятие используется при проектном расчете размерной цепи.

В процессе обработки или при сборке изделия исходное звено получается обычно последним, замыкая размерную цепь. Такое звено называется замыкающим.

Его величина и допуск зависят от величины и точности всех остальных звеньев, называемых составляющими.

Уменьшающие и увеличивающие звенья.

Составляющие звенья, при увеличении которых увеличивается замыкающее звено, называют увеличивающими (обозначают ).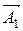

, при увеличении которых, замыкающее звено уменьшается, называется уменьшающими (обозначают ).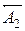

Составление размерных цепей.

При проведении размерного анализа рекомендуется выделять звенья и составлять размерные цепи, руководствуясь следующими рекомендациями:

1. Должна быть четко сформулирована задача, для решения которой рассчитывается размерная цепь.

2. Для выявления исходного звена необходимо установить требования к точности, которым должно удовлетворять изделие или сборочная единица.

Правильно составленная размерная цепь должна иметь:

— при мысленной разборке звенья сохраняться как размеры конкретных деталей.

Составление и расчет размерных цепей является обязательной частью конструирования и позволяют:

— установить количественную связь между размерами деталей машин;

— уточнить номинальные значения и допуски взаимосвязанных размеров;

— добиться наиболее правильной простановки размеров на чертежах;

— определить наиболее рентабельный вид взаимозаменяемости;

— определить операционные (промежуточные) размеры.

Основное уравнение размерной цепи.

Для проведения размерного анализа кроме размерной схемы необходимо составить уравнение размерной цепи, вытекающее из условия замкнутости: Если в размерную цепь входит m увеличивающих звеньев и n уменьшающих звеньев, то уравнение линейной размерной цепи имеет вид:

(1)

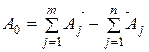
Прямая и обратная задачи.

При расчете размерных цепей могут решаться две задачи:

1. Определение допуска и предельных отклонений составляющих размеров по заданным номинальным размерам всех звеньев цепи и заданным предельным размерам исходного (замыкающего) звена. (Прямая задача или проектный расчет).

2. Определение номинального размера и допуска замыкающего звена по заданным номинальным размерам и предельным отклонениям составляющих звеньев. (Обратная задача или проверочный расчет).

Методы достижения заданной точности исходного звена.

Существуют следующие методы достижения заданной точности исходного звена (решения размерных цепей):

1. Метод полной взаимозаменяемости (максимума – минимума).

2. Теоретико-вероятностный метод.

3. Метод групповой взаимозаменяемости.

4. Метод регулирования.

1. Метод полной взаимозаменяемости.

Детали соединяются на сборке без дополнительных операций. Значения замыкающего звена не выходят за установленные пределы. Расчет размерной цепи производится методом максимума – минимума.

Простота и экономичность сборки; упрощение организации поточного сборочного процесса; возможность широкого кооперирования.

Допуски составляющих звеньев получаются наименьшими из всех методов, что может оказаться неэкономичным.

В индивидуальном и мелкосерийном производстве, при большей величине допуска на исходное звено и малом числе составляющих звеньев.

Выбор метода решения размерных цепей.

При выборе метода решения размерных цепей необходимо учитывать:

· Функциональное назначение изделия;

· Его конструктивные и технологические особенности;

· Стоимость изготовления и сборки;

· Тип производства и другие факторы.

Заданная точность исходного звена должна достигаться с наименьшими технологическими и эксплуатационными затратами.

При прочих равных условиях рекомендуется в первую очередь выбирать такие методы решения размерных цепей, при которых сборка производиться без подбора, пригонки и регулирования, т.е. методы полной взаимозаменяемости и вероятностный.

Если применение этих методов экономически нецелесообразно или технически невозможно, следует перейти к использованию одного из методов неполной взаимозаменяемости.

При выборе метода расчета цепей можно ориентироваться на среднюю величину допуска составляющих звеньев или среднюю степень точности (квалитет) составляющих звеньев.

(2)

(3)

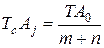
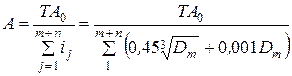
Метод полной взаимозаменяемости.

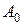
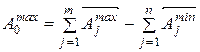
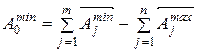
После составления уравнения размерной цепи (1) и решения его относительно можно определить предельные размеры замыкающего звена:

(4)

(5)

Вычитая почленно из (4) выражение (5) получим формулу для определения допуска замыкающего звена:

(6)

(7)

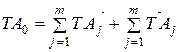
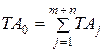
Анализируя формулу (7) можно сделать следующие выводы:

1. В качестве замыкающего звена при сборке или изготовлении необходимо принимать наименее ответственный размер.

2. Точность замыкающего звена увеличивается с уменьшением допусков составляющих звеньев.

3. Сокращение числа звеньев приводит к повышению точности замыкающего звена; чем меньше число составляющих, тем больше допуски на составляющие звенья при той же величине допуска на исходное (замыкающее) звено, тем меньше стоимость изготовления.

Если из уравнений (4) и (5) вычесть последовательно уравнение (1), получим

выражения для определения предельных отклонений замыкающего (исходного) звена:

(8)

(9)

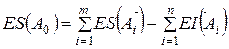
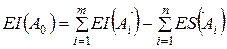
При расчете размерных цепей часто оказывается удобным оперировать не предельными отклонениями ES и EI, а средними отклонениями Е

(10)

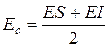
Сложив почленно уравнения (8) и (9) и учитывая (10) получим среднее отклонение поля замыкающего звена.

(11)

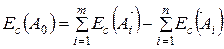
Решение прямой задачи.

Такая задача встречается гораздо чаще. Она наиболее важна, поскольку конечная цель расчета допусков составляющих размеров при заданной точности сборки (заданном допуске исходного звена) – обеспечить выполнение машиной ее функционального назначения. Эту задачу можно решать одним из следующих способов.

Способ равных допусков.

Применяется, если составляющие размеры входят в один интервал размеров и могут быть выполнены с примерно одинаковой экономической точностью.

Допуски всех составляющих звеньев принимаются одинаковыми.

(12)

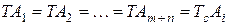
Используя уравнение (7) и равенство (12) получим выражение (2):

(2)

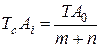
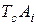
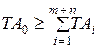
Полученный средний допуск корректируют для всех или некоторых составляющих звеньев в завасимости от их номинальных размеров, технологических возможностей изготовления, конструктивных требований. При этом должно выполняться условие:

(13)

При этом выбирают стандартные поля допусков желательно предпочтительного применения.

Способ равных допусков прост, но недостаточно точен, т.к. корректировка допусков произвольна. Его можно рекомендовать для предварительного назначения допусков составляющих размеров.

Способ допусков одного квалитета.

Применяется, если все составляющие размеры могут быть выполнены с допуском одного квалитета и допуски составляющих размеров зависят от их номинального значения.

Известны номинальные размеры всех звеньев и предельные отклонения исходного (замыкающего звена).

Требуемый квалитет определяют следующим образом:

Допуск составляющего размера: 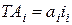, где

Используя формулу (7):

По условию 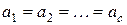. Тогда

Откуда получаем формулу (3):

(3)

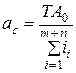
По значению 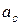выбирают ближайший квалитет. Найдя по таблицам ГОСТа 25347-82 допуски составляющих размеров, корректируют их значения. Допуски для охватывающих размеров рекомендуется определять как для основного отверстия, а для охватываемых – как для основного вала. При этом должно соблюдаться условие (13).

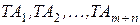
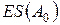
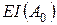
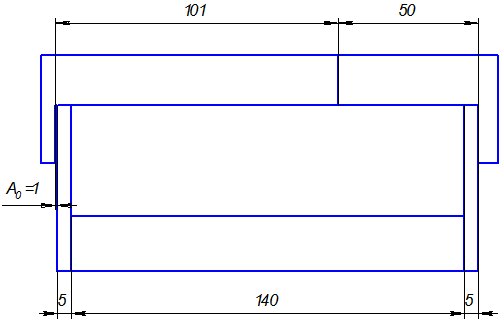
Найдя допуски по заданным отклонениям и определяют значения и знаки верхних и нижних отклонений составляющих размеров так, чтобы они удовлетворяли уравнениям (8) и (9).

Пример. Определить допуски составляющих размеров деталей сборочной единицы (см. рис.). Заданы номинальные значения составляющих размеров и предельные отклонения исходного звена:

Рисунок 1 – Схема размерной цепи

Находим номинальный размер исходного звена по (1):

Наименьший предельный размер совпадает с номинальным, поэтому:

и 0,75 мм.

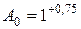
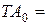
Среднее число единиц допуска в размерной цепи определяем по (3)

Для 10 квалитета а = 64

Для 11 квалитета а = 100

Устанавливаем для всех размеров цепи, кроме А₄, допуск по 11 квалитету. Допуск размера А₄ можно назначить несколько меньшим, т.к. вал по этому размеру легко обработать с высокой точностью.

По таблицам ГОСТ 25347-82 находим допуски на размеры А₁, А₂, А₃, А₅: 0,22; 0,16; 0,075; 0,075 мм; Т(А₄) = 0,25 мм; на долю размера А₄ остается допуск 0,22 мм:

ТА₄ = 0,75 – (0,22+0,16+0,075+0,075) = 0,22 мм.

Однако целесообразно принять его стандартным по 10 квалитету 0,16.

Назначаем предельные отклонения:

Проверка:0,75 мм > 0,22+0,16+0,075+0,075+0,16 = 0,69 мм

Условие (13) выполняется.

2. Теоретико – вероятный метод.

Детали соединяются на сборке, как правило, без пригонки, регулировки, подбора, при этом у небольшого (заранее принятого) количества изделий (обычно 3 изделия на 1000, процент риска 0,27) значения замыкающих звеньев могут выйти за установленные пределы. Расчет размерной цепи производится вероятностным методом.

Те же, что и у метода полной взаимозаменяемости плюс экономичность изготовления деталей за счет расширенных полей допусков (по сравнению с предыдущим методом).

Возможны, хотя и маловероятны, дополнительные затраты на замену или подгонку некоторых деталей.

В серийном и массовых производствах; при малом допуске исходного звена и большом числе составляющих звеньев.

Расчет размерных цепей теоретико – вероятностным методом.

Этот метод базируется на основных зависимостях метода максимума – минимума. Однако он учитывает более реальное распределение размеров в пределах поля допуска. В теории размерных цепей наиболее часто применяются следующие основные законы рассеивания размеров деталей: а) нормальный закон (закон Гаусса); б) закон треугольника (закон Симсона).

Уравнение (7) для определения допуска замыкающего (исходного) звена при расчете ТВМ принимает вид:

(14)

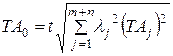
где 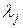— коэффициент относительного рассеивания, зависящий от закона рассеивания.

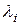
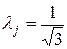
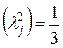
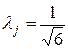
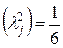
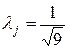
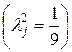
При расчетах коэффициент принимают равным:

, если ничего не известно о характере кривой рассеивания размеров деталей (мелкосерийное и индивидуальное производство);

, если предполагается, что рассеивание размеров деталей близко к закону треугольника;

, если кривая рассеивания имеет нормальный характер (крупносерийное и массовое производство)

t – коэффициент, зависящий от % риска Р, принимаемый по таблице.

Рассмотрим пример. Для линейной размерной цепи, состоящей из 5 звеньев:

По методу max – min:

По методу ТВМ: 0,27%:

0,01%:

32%:

Таким образом для линейных цепей при нормальном законе распределения размеров деталей (Р = 0,27%)

(15)

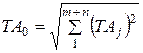
Способ равных допусков.

(16)

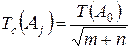
Способ допусков одного квалитета.

(17)

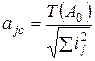
Решим нашу задачу (см. рис. выше).

Пример.

Таким образом ТВМ позволяет назначить более широкие допуски на составляющие звенья, чем метод max – min.

Источник