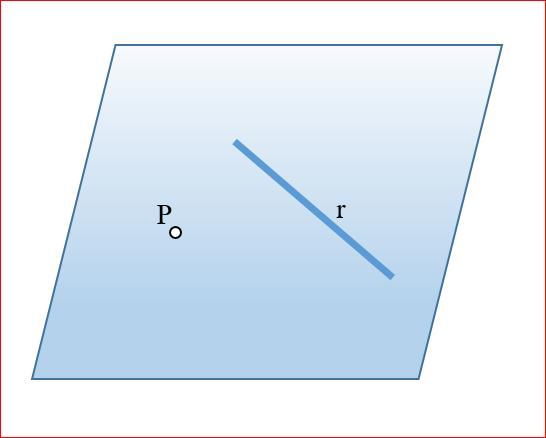
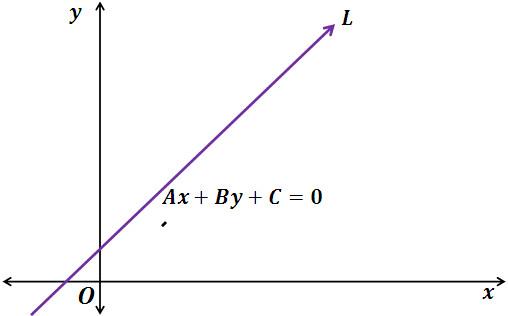Что называется расстоянием между точкой и прямой
Расстояние от точки до прямой
Базовые понятия
Расстоянием есть такая величина, которая характеризует отдаленность объектов друг от друга. Это определение применимо для плоскости и для пространства. Рассмотрим пример. Допустим у нас есть две точки, изображенные на рисунке:
Нужно узнать расстояние от одной точки до другой. Для этого можно воспользоваться каким-либо измерительным инструментом, к примеру, линейкой. Прикладываем ее началом к одной точке и соединяем с другой, на шкале мы увидим значение, которое и будет равно расстоянию между точками.
Для определения можно применять также циркуль, при этом циркулем измеряют расстояние, его прикладывают к линейке или другому инструменту со шкалой расстояния, и получают значение.
Рассмотрим пример решения задачи по определению расстояния между точкой и прямой.
Определения расстояния между точкой и прямой
Если у нас есть прямая и точка, что не находится на ней, то согласно аксиомы геометрии мы знаем, что они образуют некую плоскость, именно поэтому мы можем решать эту задачу используя понятия планиметрии.
Теорема о создании единственной плоскости при помощи точки и прямой выводится из аксиомы о трех точках, описывающих плоскость. Ведь на прямой возможно выбрать две случайные точки, а третья у нас тоже есть.
Расстояние от точки до прямой – это перпендикулярный отрезок, соединяющий точку и прямую.
Разберем подробнее понятие о расстоянии между точкой и прямой на конкретном примере.
Определение расстояния между точкой и прямой в плоскости
Распространенными задачами на эту тему как в плоскости, так и в пространстве, есть задачи на определение расстояния при известных координатах точки и уравнении прямой.
Практически не всегда удобно графически решать данные задачи, поэтому их решают аналитическим путем.
Не нашли что искали?
Просто напиши и мы поможем
Разберем решение подобной задачи в плоскости.
Задано уравнение прямой \(a: y=3x+2\) и точка \(M\) с координатами (2;0). Необходимо определить расстояние от точки до прямой.
Имея запись в такой форме не сложно определить, что вектор нормали к этой прямой будет иметь координаты (3;-1). Этот же вектор есть направляющим для нашего перпендикуляра.
Также мы знаем, что наш перпендикуляр пересекается с прямой через точку \(M\) с координатами (2;0). Значит мы можем привести это уравнение к виду:
Выразив y из второго уравнения и подставив его в первое, получаем:
Решаем это уравнение:
Подставив найденное значение во второе уравнение, находим \(y\) :
В итоге, мы определили координаты точки пересечения прямой и перпендикуляра. Они равны (-0.4;0.8).
Определим длину отрезка \(MD\) :
Ответ: расстояние от точки \(M\) до прямой a равняется 0,89.
Определение расстояние от точки до прямой в пространстве
Для расчета расстояния между точкой и прямой в пространстве пользуются такой формулой:
где \(x_0, y_0, z_0\) – координаты заданной точки;
\(x_1, y_1, z_1\) – координаты вектора нормали заданной прямой;
\( l, m_1, n_1\) – координаты направляющего вектора прямой.
Эта формула аналогична уравнению для плоскости, но представляется сложнее. В расчетах нет ничего сложного, если владеть принципами решения матричных выражений.
Сложно разобраться самому?
Попробуй обратиться за помощью к преподавателям
Разберем решение задачи с применением этой формулы.
Направляющий вектор прямой m имеет координаты (1;2;4), а вектор нормали (-5;-1;4).
Подставив все значения в формулу расчета, получим:
В ответе получаем, что расстояние в пространстве между точкой \(K\) и прямой \(m\) составляет 5,080.
Не нашли нужную информацию?
Закажите подходящий материал на нашем сервисе. Разместите задание – система его автоматически разошлет в течение 59 секунд. Выберите подходящего эксперта, и он избавит вас от хлопот с учёбой.
Гарантия низких цен
Все работы выполняются без посредников, поэтому цены вас приятно удивят.
Доработки и консультации включены в стоимость
В рамках задания они бесплатны и выполняются в оговоренные сроки.
Вернем деньги за невыполненное задание
Если эксперт не справился – гарантируем 100% возврат средств.
Тех.поддержка 7 дней в неделю
Наши менеджеры работают в выходные и праздники, чтобы оперативно отвечать на ваши вопросы.
Тысячи проверенных экспертов
Мы отбираем только надёжных исполнителей – профессионалов в своей области. Все они имеют высшее образование с оценками в дипломе «хорошо» и «отлично».
Гарантия возврата денег
Эксперт получил деньги, а работу не выполнил?
Только не у нас!
Деньги хранятся на вашем балансе во время работы над заданием и гарантийного срока
Гарантия возврата денег
В случае, если что-то пойдет не так, мы гарантируем возврат полной уплаченой суммы
Отзывы студентов о нашей работе




























«Всё сдал!» — безопасный онлайн-сервис с проверенными экспертами
Используя «Всё сдал!», вы принимаете пользовательское соглашение
и политику обработки персональных данных
Сайт работает по московскому времени:
Принимаем к оплате 


Расстояние от точки до прямой — формулы и способы определения
Точка и прямая
Прежде чем говорить, как найти расстояние от прямой до точки, необходимо подробно рассмотреть, о каких элементах идет речь.
Известно, что в двумерном или трехмерном пространстве в геометрии для определения места расположения того или иного объекта вводится специальная система координат. Удобнее всего использовать прямоугольную декартову систему, которая представляет собой пересекающиеся под прямым углом оси (2 для плоскости и 3 для трехмерного пространства). На каждой из них существует шкала в выбранных единицах.
Обычно она является равномерной, то есть на каждой оси единица представляет собой отрезок одинаковой длины.
Точечный объект
Или просто точка. Это нульмерный объект, который в двумерном пространстве представляет собой набор двух координат, а в трехмерном — трех. Математически точка записывается так: A (x1; y1), где x1 — ее координата по оси x, y1 — по оси y. Для определения значения координат необходимо от точки провести перпендикуляр к соответствующей оси, их пересечение укажет на искомое значение. Примеры разных точек на плоскости и пространстве:

Точка P лежит на оси x, а M в начале координатной системы. Обе они заданы на плоскости, в отличие от Q и N, которые можно построить в пространстве. Также следует отметить, что у координатных осей имеется положительное и отрицательное направления, поэтому точки могут иметь отрицательные координаты.
Уравнения линии
Прямая линия является одним из самых распространенных объектов в геометрии. С помощью нее строятся многие симметричные фигуры, например, пирамида, призма, треугольник, прямоугольник (но не сфера). Прямая линия представляет собой бесконечный объект в одном направлении, и нульмерный в двух других, если речь идет об объемном пространстве.
Для выполнения математических операций с геометрическим элементом существуют разные виды уравнений, которые его задают. Среди них можно назвать:
Чаще всего в задачах применяют первые 2 вида. Универсальным уравнением, которое можно с легкостью преобразовать в любые другие формы, является векторное. Задается для трехмерного случая оно следующим образом:
(x; y; z) = (x0; y0; z0) + α*(vx; vy; vz).

Здесь (x; y; z) — координаты произвольной точки, которая принадлежит заданной прямой, (x0; y0; z0) — известная точка, лежащая на объекте, v (vx; vy; vz) — вектор, параллельно которому проходит прямая, он называется направляющим, α — произвольный числовой параметр, который может иметь положительные или отрицательные значения. Очевидно, что для плоского случая количество координат для каждого элемента будет равно двум.
Векторным уравнением удобно пользоваться, поскольку его легко преобразовать в параметрическое или в отрезках. В первом случае получается следующая система:
Для уравнения в отрезках получается такое равенство:
(x-x0)/vx = (y-y0)/vy = (z-z0)/vz.
Чтобы получить из векторной формы уравнение общего типа для случая на плоскости, достаточно написать выражение в отрезках, а затем из него выразить y через x. В итоге получается такой вид:
Для трехмерного пространства также можно использовать этот математический прием, однако придется выражать не только y через x, но и z через, например, y. Дело в том, что в объемном пространстве прямая задается в общем виде как пересечение двух плоскостей.
Способы определения расстояния
В первую очередь необходимо понять, что называется дистанцией между точкой и прямой линией. Пусть имеется прямая a и точка A. Если из нульмерного объекта провести отрезок к прямой так, чтобы ее он пересекал под прямым углом в некоторой точке A1, то AA1 будет называться перпендикуляром к a. Согласно определению, расстояние от точки до прямой равно длине перпендикулярного отрезка, опущенного из нульмерного объекта к одномерному.

Из геометрических представлений понятно, что длина AA1 будет наименьшей среди всех возможных отрезков, которые можно провести от A к a.
Применение векторных выражений
После получения представлений, что понимают под дистанцией между геометрическими объектами, в докладе можно переходить к рассмотрению первого универсального способа решения этой задачи.
Пусть имеется прямая, заданная в векторной форме в двумерном пространстве: (x; y) = (x0; y0) + α*(vx; vy).
В этой же координатной системе задана точка P (x1; y1). В первую очередь необходимо найти вектор u (ux; uy), который будет перпендикулярен направляющему v (vx; vy). Сделать это несложно, если вспомнить, что скалярное произведение перпендикулярных векторов равно нулю. В итоге получается следующее выражение:
Подставляя в это равенство произвольное значение uy, можно получить координату ux. Если одна из координат вектора v равна нулю, например, vx=0, тогда uy=0 для любых значений ux отличных от 0.
Зная координаты направляющего вектора u для перпендикуляра, можно построить для него векторное уравнение прямой, которая будет проходить через P:
(x; y) = (x1; y1) + β *(ux; uy).
Теперь необходимо найти точку пересечения обеих прямых. Для этого можно выразить y через x для каждой из них, а затем, решить систему из двух линейных уравнений. Например, получилась точка Q (x2; y2).
Для решения задачи остается сделать последний шаг: найти длину отрезка, заключенного между точками P и Q. Искомая формула имеет вид:
PQ = ((x2-x1)^2 + (y2-y1)^2)^0,5.
Описанный способ определения дистанции от прямой до точки можно использовать для задач на плоскости. Дело в том, что в трехмерном пространстве существует бесконечное количество перпендикуляров заданной прямой, поэтому для трехмерного случая придется вводить еще одно условие на поиск перпендикулярного отрезка: он должен лежать в плоскости, проходящей через заданные прямую и точку. Этот факт усложняет решение задачи.
Использование формулы
Применение известной формулы для решения геометрических проблем является самым простым способом. Пусть имеется некоторая прямая, которая в векторной форме задается так:
(x; y; z) = (x0; y0; z0) + α*(vx; vy; vz).

Известна также точка P (x1; y1; z1). Теперь следует выбрать произвольную точку на прямой, пусть это будет Q (x2; y2; z2). Следует отметить, что координаты Q удовлетворяют векторному уравнению заданной прямой. Далее, нужно построить вектор PQ, его координаты определяются так:
PQ = (x2-x1; y2-y1; z2-z1).
После этого следует рассмотреть параллелограмм, который однозначно может быть построен на векторах PQ и v (vx; vy; vz) — направляющий отрезок заданной прямой линии (для наглядности фигуру можно изобразить на рисунке). Известно, что площадь параллелограмма может быть определена двумя способами:
Поскольку оба выражения используются для нахождения одной и той же площади S, их можно приравнять и выразить высоту h:
Поскольку высота параллелограмма является искомой дистанцией d от точки P до заданной в задаче прямой, получается следующая простая формула:
Вычисление векторного произведения проще всего выполнять с помощью матрицы и алгебраического дополнения (стандартная операция вычисления определителя). Удобство полученной формулы заключается в ее универсальности, то есть она применима как для трехмерного пространства, так и для случая на плоскости. Для двумерной задачи в координатной форме выражение примет вид:
d = ((x2-x1)*vy+(y2-y1)*vx)/ (vx 2 + vy 2 )^0,5.
Это выражение является несколько громоздким, поэтому рекомендуется запомнить только его векторную форму.
Решение задачи

Для начала нужно находить направляющий вектор прямой. Его координаты будут соответствовать следующим значениям:
Теперь следует найти вектор AC:
AC = C — A = ((-1−1); (1−0)) = (-2; 1).
Прежде чем воспользоваться формулой для определения расстояния, можно заранее вычислить модуль векторного произведения [AB*AC] и длину AB:
Тогда дистанция d от точки C до прямой, проходящей через A и B будет равно:
Таким образом, для определения расстояния между известными прямой и точкой в пространстве существует 2 способа.

Первый предполагает использование ряда математических рассуждений с выкладками. Он справедлив только для задач на плоскости. Второй способ позволяет воспользоваться универсальной формулой.
Как находить расстояние от точки до прямой? Найти расстояние от точки М до прямой: формула
Умение находить расстояние между разными геометрическими объектами важно, когда выполняются расчеты площади поверхности фигур и их объемов. В данной статье рассмотрим вопрос о том, как находить от точки до прямой расстояние в пространстве и на плоскости.
Математическое описание прямой
Чтобы понять, как находить расстояние от точки до прямой, следует разобраться с вопросом математического задания этих геометрических объектов.

Первый вид называется векторным уравнением. Ниже приведены выражения для прямых в трехмерном и двумерном пространстве:
(x; y; z) = (x0; y0; z0) + α × (a; b; c);
(x; y) = (x0; y0 ) + α × (a; b)
Векторное уравнение удобно в том плане, что оно явно содержит вектор направления прямой, координаты которого можно использовать при решении задач параллельности или перпендикулярности разных геометрических объектов, например двух прямых.
Второй вид уравнения, который мы рассмотрим для прямой, называется общим. В пространстве этот вид задается общими уравнениями двух плоскостей. На плоскости же он имеет следующую форму:
Когда выполняют построение графика, то его часто записывают зависимостью от икса/игрека, то есть:
Понятие о расстоянии между прямой и точкой
Разобравшись с уравнениями, можно непосредственно переходить к ответу на вопрос о том, как находить от точки до прямой расстояние. В 7 классе школы начинают рассматривать этот вопрос с определения соответствующей величины.
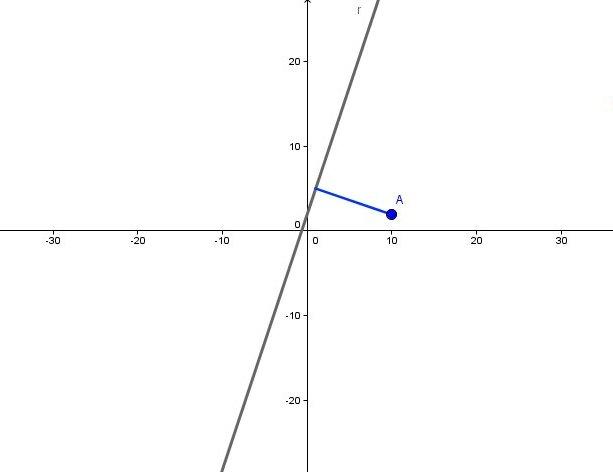
Расстоянием между прямой и точкой называется длина перпендикулярного этой прямой отрезка, который опущен из рассматриваемой точки. Ниже на рисунке изображена прямая r и точка A. Синим цветом показан перпендикулярный прямой r отрезок. Его длина является искомым расстоянием.
Здесь изображен двумерный случай, тем не менее данное определение расстояния справедливо и для трехмерной задачи.
Необходимые формулы
В зависимости от того, в каком виде записано уравнение прямой и в каком пространстве решается задача, можно привести две основные формулы, дающие ответ на вопрос о том, как найти расстояние между прямой и точкой.
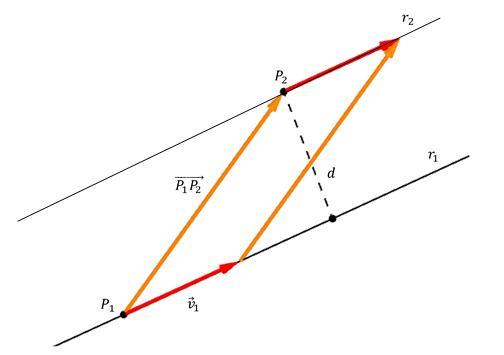
Обозначим известную точку символом P2. Если уравнение прямой задано в векторном виде, то для d расстояния между рассматриваемыми объектами справедлива формула:
То есть для определения d следует вычислить модуль векторного произведения направляющего для прямой вектора v¯ и вектора P1P2¯, начало которого лежит в произвольной точке P1 на прямой, а конец находится в точке P2, затем поделить этот модуль на длину v¯. Эта формула является универсальной для плоского и трехмерного пространства.
Если задача рассматривается на плоскости в системе координат xy и уравнение прямой задано в общем виде, тогда следующая формула найти расстояние от прямой до точки позволяет так:
Прямая: A × x + B × y + C = 0;
Расстояние: d = |A × x2 + B × y2 + C| / √(A2 + B2)
Приведенная формула является достаточно простой, однако ее использование ограничено отмеченными выше условиями.
Координаты проекции точки на прямую и расстояние
Ответить на вопрос о том, как находить расстояние от точки до прямой, можно также другим способом, не предполагающим запоминание приведенных формул. Этот способ заключается в определении точки на прямой, которая является проекцией исходной точки.
Предположим, что имеется точка M и прямая r. Проекция на r точки M соответствует некоторой точке M1. Расстояние от M до r равно длине вектора MM1¯.
Как найти координаты M1? Очень просто. Достаточно вспомнить, что вектор прямой v¯ будет перпендикулярен MM1¯, то есть их скалярное произведение должно быть равным нулю. Добавляя к этому условию тот факт, что координаты M1 должны удовлетворять уравнению прямой r, мы получаем систему простых линейных уравнений. В результате ее решения получаются координаты проекции точки M на r.
Описанная в этом пункте методика нахождения расстояния от прямой до точки может использоваться для плоскости и для пространства, однако ее применение предполагает знание векторного уравнения для прямой.
Задача на плоскости
Теперь пришло время показать, как использовать представленный математический аппарат для решения реальных задач. Предположим, что на плоскости задана точка M(-4; 5). Необходимо расстояние найти от точки М до прямой, которая описывается уравнением общего вида:
Рекомендуется сразу проверить, принадлежит ли М этой прямой, поскольку в таком случае искомое расстояние будет равно нулю. Подставляем координаты:
То есть M не лежит на прямой.
Поскольку уравнение прямой задано не в общем виде, приведем его к таковому, чтобы иметь возможность воспользоваться соответствующей формулой, имеем:
Теперь можно подставлять известные числа в формулу для d:
d = |A × x2 + B × y2 + C| / √(A2+B2) =
Задача в пространстве
Теперь рассмотрим случай в пространстве. Пусть прямая описывается следующим уравнением:
Так же, как и в предыдущем случае, проверим принадлежность M заданной прямой. Для этого подставим координаты в уравнение и перепишем его в явном виде:
Поскольку получены разные параметры α, то M не лежит на этой прямой. Рассчитаем теперь расстояние от нее до прямой.
Вычислим векторное произведение между PM¯ и направляющим вектором прямой v¯. Получаем:
Теперь подставляем модули найденного вектора и вектора v¯ в формулу для d, получаем:
d = √(9 + 64 + 49) / √(9 + 4 + 1) ≈ 2,95
Этот ответ можно было получить, воспользовавшись описанной выше методикой, предполагающей решение системы линейных уравнений. В этой и предыдущей задачах вычисленные значения расстояния от прямой до точки представлены в единицах соответствующей системы координат.