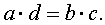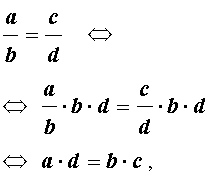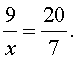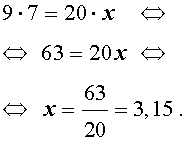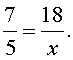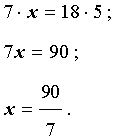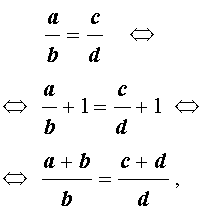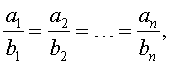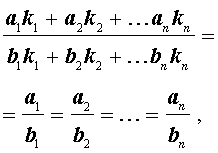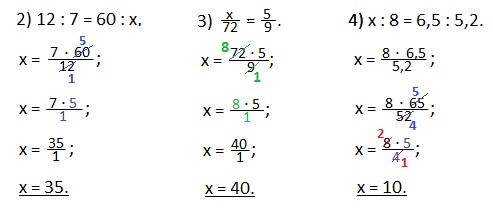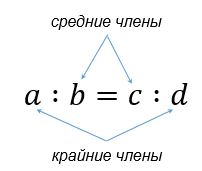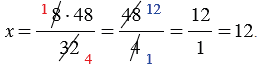Что называется пропорцией сформулируйте свойства пропорции
Пропорции, члены пропорции, основное свойство пропорции
Содержание
Пропорции, члены пропорции. Основное свойство пропорции
Число a называют предыдущим членом отношения, число b – последующим членом отношения.
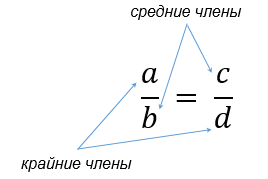
Пропорцией называют равенство двух отношений:
.
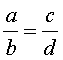
Иногда пропорцию записывают так:
И в одной, и во второй формах записи пропорции числа a и d называют крайними членами пропорции, а числа b и c – средними членами пропорции.
Для любой пропорции справедливо следующее равенство, которое называют основным свойством пропорции:
Словесно это равенство можно сформулировать так: произведение крайних членов пропорции равно произведению средних членов пропорции.
Для того, чтобы доказать основное свойство пропорции, умножим пропорцию на выражение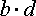 
.
В результате получим:
что и требовалось доказать.
Основное свойство пропорции позволяет по трем любым известным членам пропорции найти четвертый неизвестный член пропорции. Покажем это на двух примерах.
ОТВЕТ :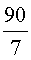 
.
Из основного свойства пропорции легко вытекают также свойства пропорции, которые называют перестановкой членов пропорции. Эти свойства формулируются так: если
.
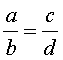
Производные пропорции
Справедливы также свойства пропорции, которые называют производными пропорциями. Эти свойства формулируются так: если
,
 |  , |
|  , |
|  , |
|  , |
|  , |
|  |
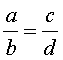
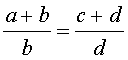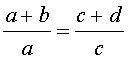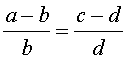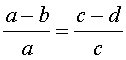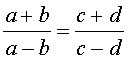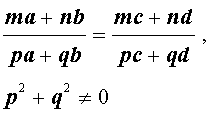В качестве примера докажем первое из указанных свойств (остальные свойства доказываются аналогично). Для этого к обеим частям пропорции
.
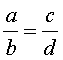
достаточно прибавить 1. В результате получаем,
Свойства равных отношений
Если выполнено соотношение
то выполнено и соотношение
– произвольные числа, которые не могут все одновременно равняться нулю.
6.1.1. Пропорция. Основное свойство пропорции
Равенство двух отношений называют пропорцией.
Тема: «Отношение» рассмотрена на предыдущем занятии («6.1. Отношение»).
Основное свойство пропорции.
Произведение крайних членов пропорции равно произведению ее средних членов.
Чтобы найти неизвестный крайний член пропорции, нужно произведение средних членов пропорции разделить на известный крайний член.
Примеры. Найти неизвестный крайний член пропорции.
1) х : 20 = 2 : 5. У нас х и 5 — крайние члены пропорции, а 20 и 2 — средние.
Решение.
х = (20·2):5 — нужно перемножить средние члены (20 и 2) и результат разделить на известный крайний член (число 5);
х = 40 : 5 — произведение средних членов (40) разделим на известный крайний член (5);
х = 8. Получили искомый крайний член пропорции.
Удобнее записывать нахождение неизвестного члена пропорции с помощью обыкновенной дроби. Вот как тогда запишется рассмотренный нами пример:
Искомый крайний член пропорции (х) будет равен произведению средних членов (20 и 2), деленному на известный крайний член (5).
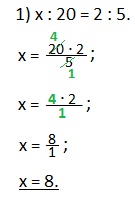
Сокращаем дробь на 5 (делим на 5 и числитель и знаменатель дроби). Находим значение х.
Если забыли, как сокращать обыкновенные дроби, то повторите тему: «5.4.2. Примеры сокращения обыкновенных дробей»
Еще такие примеры на нахождение неизвестного крайнего члена пропорции.
Чтобы найти неизвестный средний член пропорции, нужно произведение крайних членов пропорции разделить на известный средний член.
Примеры. Найти неизвестный средний член пропорции.
5) 9 : х = 3 : 14. Число 3 — известный средний член данной пропорции, числа 9 и 14 — крайние члены пропорции.
Решение.
х = (9·14):3 — перемножим крайние члены пропорции и результат разделим на известный средний член пропорции;
х= 136:3;
Решение этого примера можно записать иначе:
Искомый средний член пропорции (х) будет равен произведению крайних членов (9 и 14), деленному на известный средний член (3).
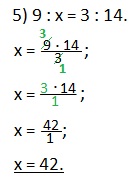
Сокращаем дробь на 3 (делим на 3 и числитель и знаменатель дроби). Находим значение х.
Если забыли, как сокращать обыкновенные дроби, то повторите тему: «5.4.2. Примеры сокращения обыкновенных дробей»
Еще такие примеры на нахождение неизвестного среднего члена пропорции.
Что такое пропорция
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое пропорция
Пропорция — это равенство двух отношения.
Пропорциональный — это такой, который находится в определенном отношении к какой-либо величине.
Пропорция всегда содержит равные коэффициенты.
Если выразить определение формулой, то выглядеть оно будет так:
a и d — крайние члены пропорции
Читается это выражение так: a так относится к b, как c относится к d
Например:
Это равенство двух отношений: 15 так относится к 5, как 9 относится к 3.
15 и 3 — крайние члены пропорции.
5 и 9 — средние члены пропорции.
Наглядный пример для понимания:
У нас есть восемь кусочков аппетитной пиццы и, предположим, четыре голодных друга.
Это значит, что 8 аппетитных кусочков пиццы будут так относиться к 4 голодным друзьям, что каждому голодающему достанется по 2 кусочка. Прекрасно!
А теперь представим, ситуацию, в которой есть только половина аппетитной пиццы, но при этом и голодных друга — всего два.
Что мы имеем: 4 кусочка и 2 друга, претендующих на них.
Это значит, что 4 аппетитных кусочка будут так относиться к 2 голодным друзьям, что каждому из них достанется по 2 кусочка.
Оценив обе ситуации, делаем вывод, что отношение 8/4 пропорционально отношению 4/2. Отношения в пропорции — равные.
Вывод: знание математических пропорций пригодится при заказе пиццы. Быстренько прикидываем отношение количества человек, претендующих на пиццу, и число кусочков — и сразу заказываем побольше пиццы, чтобы никто не остался голодным😉
Основное свойство пропорции
Запомните основное свойство пропорции:
Произведение крайних членов пропорции равно произведению средних членов этой пропорции.
В виде формулы свойство выглядит так:
a : b = c : d = a * d = b * c
Мы знаем, что a и d — крайние члены пропорции, b и c — средние.
Это свойство следует применять, чтобы проверить пропорцию. Если все сходится согласно формулировке — пропорция составлена верно, и отношения в пропорции являются равными друг другу.
Давайте проверим несколько пропорций.
Пример 1. Дана пропорция:6/2 = 12/4
Делаем вывод, что пропорция 6/2 = 12/4 составлена верно.
Пример 2. Дана пропорция: 10/2 = 16/4
Отсюда делаем вывод, что отношения в пропорции 10/2 ≠ 16/4 не являются равными.
Примеры решения задач с пропорцией
Чтобы потренироваться в составлении пропорций, решим вместе несколько задачек.
Задачка 1. Дана математическая пропорция: 15/3 = x/4
Ответ: в пропорции 15/3 = x/4, x = 20
Задачка 2. Найдите четвертый член пропорции: 18, 9 и 24.
Ответ: четвертый член пропорции — 12.
Задачка 3. 18 человек могут съесть пять килограммов суши за 8 часов, сколько часов понадобится 9 людям?
Ответ: 16 часов понадобится 9 людям, чтобы съесть все суши.
Задачка 4. Дана пропорция: 20/2 = y/4
Пропорции
Буквенная запись пропорции:
или 
.
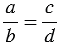
Читают пропорцию так: «отношение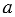 
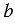
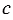
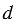
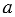
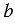
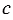
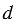
к 
равно отношению отношению 
к 
» или » относится к , как относится к «.
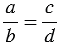
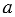
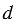
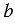
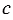
Числа, входящие в пропорцию , имеют специальные названия: и — крайние члены пропорции, и — средние члены пропорции. Происхождение этих терминов вытекает из строчной записи пропорции: .
Основное свойство пропорции:
| Произведение крайних членов пропорции равно произведению ее средних членов. |
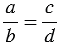
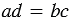
Буквенная запись свойства: если , то 
.
Если основное свойство пропорции выполняется, то говорят, что пропорция верная.
С помощью основного свойства пропорции любой ее член можно выразить через три других. Это позволяет по трем известным членам пропорции находить неизвестный.
Пример:
Найдем неизвестный член пропорции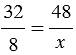 
.
Решение:
По основному свойству пропорции получим 32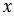 
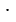
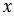
= 8
48. Откуда легко найти неизвестный множитель :
Если в верной пропорции поменять местами средние члены или крайние, то получившиеся новые пропорции тоже верны.
Пример:
1) Если — верная пропорция, то 
— верные пропорции.
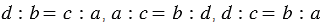
2) Если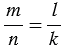 
— верная пропорция, то 
— верные пропорции.
Поделись с друзьями в социальных сетях:
Что такое пропорция: определение, элементы, основное свойство
В данной публикации мы рассмотрим, что такое пропорция, из каких элементов она состоит, а также разберем основное свойство пропорции вместе с практическим примером.
Определение пропорции
Пропорция – это равенство двух или более отношений чисел.
Допустим, у нас есть два равных отношения:
Если между этими отношениями поставить знак “равно”, то получится пропорция:
Элементы пропорции
Основное свойства пропорции
В любой верно составленной пропорции произведение крайних элементов равняется произведению средних.
Т.е. a · d = b · c.
Чтобы было проще запомнить, используется так называемое “правило крестика”, т.е. перемножение накрест лежащих элементов.
Пример
Проверим основное свойство и правило на пропорции ниже:
Оба отношения дают результат, равный одному и тому же числу (двум), следовательно, пропорция верна.
Значит мы можем перемножить ее элементы, пользуясь “правилом крестика”:
Получаем:
12 · 15 = 6 · 30 или 180 = 180