Что называется приращением независимой переменной

10.04.202214.04.2022 admin 0 Comments

Приращения независимых переменных и приращение функции

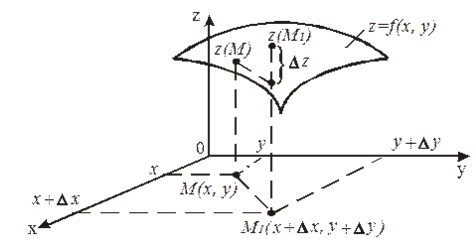
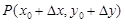
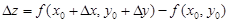
Пусть f(x, y) задана в области D и P₀(x₀, y₀) – внутренняя точка области D. Дадим аргументам x и y приращения Dx и Dy – произвольные, такие, однако, чтобы точка еще не выпала из D. Тогда

(1.4)

– полное приращение функции.

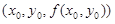
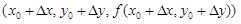
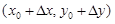
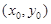
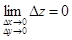
Геометрически Dz дает изменение аппликаты точки на поверхности z = f(x, y) при переходе от позиции к позиции , т.е. разность длин “столбиков”, поставленных соответственно в точках и . Условие непрерывности f(x, y) в точке (x₀, y₀) можно записать и так:

. (1.5)

Если бы мы дали приращение Dx только переменному x или только приращение Dy переменному y, то возникли бы частные приращения функции:

(1.6)

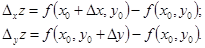
Эти приращения – частные (по x и по y соответственно); теперь оправдано и название “полное” для (1.4).

Дифференциальное исчисление функций двух переменных

Частные производные

Частными производными в точке (x₀, y₀) по x и y называются соответственно

и . (1.7)

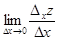
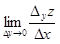
(Конечно, если эти пределы существуют.) Обозначаются они

, или , или , или (1.8)

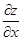
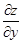
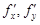
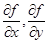
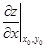
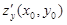
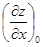
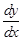
и, если необходимо, показывается точка x₀, y₀ где вычислены частные производные: или , или – например. Символы (с круглыми ¶!) – не настоящие дроби в отличие от , а лишь стилизованные обозначения пределов.

Чтобы вычислить частную производную по какому-то из переменных, надо действовать по обычным правилам дифференцирования, считая другое переменное неизменным, постоянным.

Пример 1. ;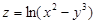

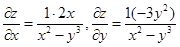
Пример 2. ;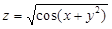

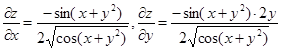
Геометрический смысл частных производных

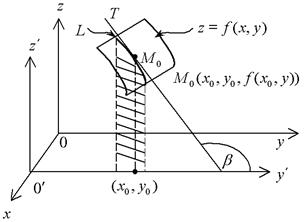
Проведем через точку (x₀, y₀) плоскость x = x₀, параллельную плоскости yOz. На рис. 6 это плоскость .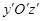

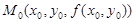
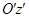
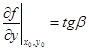
Из поверхности z = f(x, y) эта плоскость вырежет кривую L. На L получится точка – конец “столбика”, восстановленного из (x₀, y₀). Проведем через M₀ касательную прямую к линии L (в плоскости сечения). Тангенс угла наклона b касательной к оси (или, что то же, к оси Oy) и есть частная производная (по y) (рис. 6):

. (1.9)

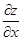
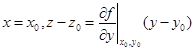
Это вытекает из геометрического смысла обычной производной. Аналогичным образом истолковывается . Касательная M₀T задается в пространстве системой двух уравнений первой степени:

. (1.10)

Совершенно аналогичным образом, если провести сечение плоскостью y = y₀, то образуется касательная прямая в этой плоскости с уравнениями

. (1.10’)

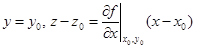
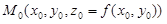
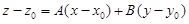
Две касательные прямые, построенные в разделе 1.2.2, определяют плоскость. Эта плоскость называется касательной плоскостью к поверхности в точке M₀. Поскольку она проходит через точку , ее уравнение можно записать так:

. (1.11)

(Проверьте, что координаты удовлетворяют (1.11).)

В сечении этой плоскости плоскостью x = x₀ образуется построенная нами касательная
прямая M₀T, для которой (см. 1.10)

. (1.12)

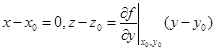
Но из (1.11) следует, что

. (1.13)

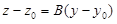
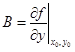
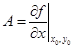
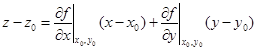
Сравнивая (1.12) и (1.13), видим, что ; точно так же находится и . Подставляя все это в (1.11), получаем:

(1.14)

– уравнение касательной плоскости.

Дата добавления: 2018-09-23 ; просмотров: 194 ; Мы поможем в написании вашей работы!

Источник

Приращение функции

Приращение функции в точке — функция обычно обозначаемая от новой переменной определяемая как

Переменная называется приращением аргумента.

В случае когда ясно о каком значении идёт речь, применяется более короткая запись.

Примеры использования

См. также

Литература

Полезное

Смотреть что такое «Приращение функции» в других словарях:

приращение функции — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN increment of function … Справочник технического переводчика

Аналитические функции — функции, которые могут быть представлены степенными рядами (См. Степенной ряд). Исключительная важность класса А. ф. определяется следующим. Во первых, этот класс достаточно широк; он охватывает большинство функций, встречающихся в… … Большая советская энциклопедия

Производная функции — У этого термина существуют и другие значения, см. Производная. Иллюстрация понятия производной Производная&# … Википедия

Нелинейные функции — Примеры линейных функций. Линейная функция функция вида f(x) = kx + b. Основное свойство линейных функций: приращение функции пропорционально приращению аргумента. То есть функция является обобщением прямой пропорциональности. График линейной… … Википедия

Дифференцируемость функции в точке — Дифференцируемая функция в математическом анализе это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так… … Википедия

Дифференциальное исчисление — Исчисление бесконечно малых, включающее так называемое Д. исчисление, а также ему обратное интегральное, принадлежит к числу наиболее плодотворных открытий человеческого ума и составило эпоху в истории точных наук. Ближайшим поводом к изобретению … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — раздел математики, в к ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу… … Математическая энциклопедия

Дифференциальное исчисление — раздел математики, в котором изучаются производные и дифференциалы функций и их применения к исследованию функций. Оформление Д. и. в самостоятельную математическую дисциплину связано с именами И. Ньютона и Г. Лейбница (вторая половина 17 … Большая советская энциклопедия

Источник

Приращение аргумента. Приращение функции

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Описание слайда:

Приращение аргумента.
Приращение функции.
МБОУ лицей №10 города Советска
Калининградской области
учитель математики
Разыграева Татьяна Николаевна

Описание слайда:

При сравнении значения функции f в некоторой фиксированной точке x₀ со значениями этой функции в различных точках x, лежащих в окрестности x₀, удобно выражать разность f(x) – f(x₀) через разность x – x₀, пользуясь понятиями «приращение аргумента» и «приращение функции».
Пусть x – произвольная точка, лежащая в некоторой окрестности фиксированной точки x₀. Разность x – x₀ называется приращением независимой переменной ( или приращением аргумента) в точке x₀ и обозначается Δx. Таким образом,
Δx = x –x₀
откуда следует, что
x = x₀ + Δx.

Описание слайда:

Говорят также, что первоначальное значение аргумента x₀ получило приращение Δx. Вследствие этого значение функции f изменится на величину
f(x) – f(x₀) = f (x₀ +Δx) – f(x₀).
Эта разность называется приращением функции f в точке x₀, соответствующим приращению Δx, и обозначается символом Δf (читается «дельта эф»), т.е. по определению
Δf = f (x₀ + Δx) – f (x₀)
откуда

f (x) = f (x₀ +Δx) = f (x₀) + Δf.

Описание слайда:

Функция y = f(x) непрерывна в точке
х = а, если в точке х = а выполняется
следующее условие:
если  х  0, то  у  0.
Пример № 2.
Для функции y = kx + m найти: а) приращение функции
при переходе от фиксированной точки х к точке х +  х;
б) предел отношения приращения функции к приращению
аргумента, при условии, что приращение аргумента
стремится к нулю.
Решение.

Описание слайда:

Имеем:
f(x) = kx + m
f(x + x) = k(x + x) + m
y = f(x + x) – f(x) = (k(x + x) + m) – (kx + m)
y = (kx + kx + m) – (kx + m) = k·x.
y = k·x.
Имеем:

Описание слайда:

Итак, для заданной функции y = x² получили:

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Охрана труда

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

Курс профессиональной переподготовки

Охрана труда

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителям истории предлагают предоставить право бесплатно посещать музеи

Время чтения: 2 минуты

ВПР для школьников в 2022 году пройдут весной

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

В России планируют создавать пространства для подростков

Время чтения: 2 минуты

МГУ откроет первую в России магистерскую программу по биоэтике

Время чтения: 2 минуты

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Частное и полное приращение функции

Вы будете перенаправлены на Автор24

Таким образом, имеем:

Записать частные и полное приращение функции

Решение:

По определению частного приращения найдем:

По определению полного приращения найдем:

Готовые работы на аналогичную тему

Решение:

По определению частного приращения найдем:

По определению полного приращения найдем:

\[\Delta _ z=(1+0,1)\cdot 2=2,2\] \[\Delta _ z=1\cdot (2+0,1)=2,1\] \[\Delta z=(1+0,1)\cdot (2+0,1)=1,1\cdot 2,1=2,31.\]

Проверить утверждение замечания для функции

Решение:

\[\Delta _ z+\Delta _ z=x+\Delta x+y+(x+y+\Delta y)=2\cdot (x+y)+\Delta x+\Delta y.\]

\[2\cdot (x+y)+\Delta x+\Delta y\ne x+\Delta x+y+\Delta y,\]

\[\Delta _ z+\Delta _ z\ne \Delta z.\]

Для функции от трех и более переменных, аналогично как для функции двух переменных определяются частные приращения по каждой из переменных:

Записать частные и полное приращение функции

Решение:

По определению частного приращения найдем:

По определению полного приращения найдем:

Решение:

По определению частного приращения найдем:

По определению полного приращения найдем:

\[\Delta _ w=(1+0,1)\cdot 2\cdot 1=2,2\] \[\Delta _ w=1\cdot (2+0,1)\cdot 1=2,1\] \[\Delta _ w=1\cdot 2\cdot (1+0,1)=2,2\] \[\Delta z=(1+0,1)\cdot (2+0,1)\cdot (1+0,1)=1,1\cdot 2,1\cdot 1,1=2,541.\]

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 17 03 2021

Источник