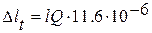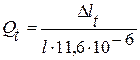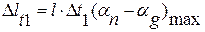Что называется предельной погрешностью

Предельная погрешность измерения и ее составляющие

Когда решается вопрос выбора конкретных универсальных измерительных средств и оценивается ожидаемая погрешность измерения, необходимо руководствоваться двумя принципиальными положениями:

1. Измерительными средствами одного вида можно выполнять измерения с различной погрешностью в зависимости от методов и условий проведения измерений.

2. Для решения вопроса выбора конкретных видов измерительных средств и условий проведения измерений необходимо оценить возможные предельные погрешности измерения.

В общем можно сказать, что на погрешность измерения оказывает влияние погрешность средств измерения и те условия, в которых производятся измерения.

Ряд слагаемых погрешностей:

— погрешности, зависящие от средств измерения;

— погрешности, зависящие от установочных мер;

— погрешности, зависящие от измерительного усилия;

— погрешности, происходящие от температурных деформаций;

— погрешности, зависящие от отклонения геометрической формы установочных мер и измеряемых деталей.

1. Погрешности, зависящие от средств измерения.

Нормируемую допустимую погрешность измерительного средства следует рассматривать как погрешность измерения при одном из возможных вариантов использования этого измерительного средства.

2. Погрешности, зависящие от установочных мер.

Погрешность измерения будет меньше, если установочная мера будет максимально подобна измеряемой детали по конструкции, массе, материалу. Погрешности от концевых мер длины возникают из-за погрешности их изготовления, включая измерение (классы), или погрешности аттестации (разряды), а также из-за погрешности от притирки.

3. Погрешности, зависящие от измерительного усилия.

При оценке влияния измерительного усилия на погрешность измерения необходимо выделять упругие деформации установочного узла и деформации в зоне контакта измерительного наконечника с деталью.

4. Погрешности, происходящие от температурных деформаций.

Для оценки влияния температурных деформаций на погрешность измерения необходимо выделять упругие деформации установочного узла и деформации в зоне контакта измерительного наконечника с деталью.

Температурный режим есть условная, выраженная в градусах Цельсия разность температур объекта измерения и измерительного средства, которая при определенных идеальных условиях вызовет ту же температурную погрешность, что и весь комплекс реально существующих причин.

В соответствии с данными определения погрешность, зависящую от температурных деформаций, при известном температурном режиме определяют по формуле:

где 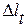— погрешность, зависящая от температурных деформаций;

l – измеряемый размер;

Q – температурный режим.

Если известна составляющая погрешности измерения, зависящая от температурных деформаций, то температурный режим в градусах можно определить по формуле:

Существуют два основных источника, обуславливающих погрешность от температурных деформаций:

— отклонение температуры воздуха от 20º С;

— кратковременные колебания температуры воздуха в процессе измерения.

Максимальное влияние отклонений температуры.

На погрешность измерения 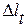можно рассчитать по формуле:

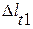
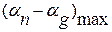
где — отклонение температуры от 20º С;

– максимально возможная разность значений коэффициентов линейного расширения материала прибора и детали.

5. Погрешности субъективные.

Из перечисленных погрешностей представляется возможным учесть только субъективную погрешность отсчитывания.

Общие положения сводятся к тому, что во всех случаях, когда обеспечиваются погрешности измерения, не превышающие цены деления, необходимо принимать меры для уменьшения погрешностей отсчитывания от параллакса, т.е. более тщательно снимать отсчет и по возможности под одним углом к указателю.

Погрешность присутствия проявляется в виде влияния теплоизлучения оператора на температуру окружающей среды, а тем самым и на измерительное средство.

Погрешность действия – погрешности, вносимые оператором при настройке прибора, подготовке объекта измерения или установочных мер; погрешности от притирки концевых мер длины; при перемещении прибора относительно детали или детали относительно элементов прибора (при измерении внутренних размеров).

Профессиональные погрешности связаны с квалификацией оператора, с отношением его к процессу измерения. Профессия создает оператора определенный навык, ответственность за производимые измерения. Характер и точность выполняемых работ определяют тот объем информации, который оператор воспринимает от измерительных средств.

6. Определение предельной погрешности измерения.

Определяют числовое значение погрешности измерения от всех составляющих.

2.Влияние погрешности измерения на результаты разбраковки.

При приемочном контроле погрешность измерения «взаимодействует» с истинными размерами и оказывает качественное влияние на окончательные результаты измерения только тех деталей, у которых размеры находятся близко к границам поля допуска, т.е. оценивает брак или годен.

Таким образом, при приемочном контроле оказывает влияние на результаты не только погрешность измерения, но и фактический размер, который имела в этот момент контролируемая деталь.

Сочетание погрешности измерения и истинного размера контролируемой детали является событием случайным и определить результаты неправильной разбраковки при определенном сочетании можно только вероятностным путем.

Для общих расчетов удобнее выражать погрешность измерения как часть от контролируемого допуска, т.к. принимать относительную величину:

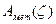
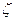
где — относительная погрешность измерения (коэффициент точности измерения);

– среднее квадратическое отклонение погрешности измерения;

Т – допуск контролируемого параметра.

Влияние точности изготовления контролируемых объектов на результаты разбраковки удобнее выразить через относительную величину, связанных как с допуском контролируемых объектов, так и с характеристикой распределения погрешности изготовления, т.е.

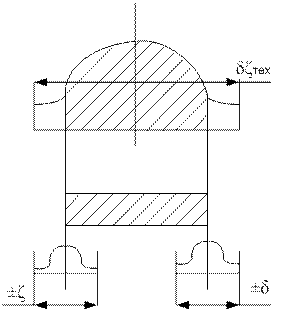
На рисунке показана взаимосвязь распределения отклонений размеров изготовленных деталей, нормируемого допуска и погрешности измерения.

Если бы применяемый метод измерения совершения не обладал погрешностью, то на кривой распределения контролируемых деталей на границах поля допуска все действительно бракованные детали оказались бы забракованными, а все детали с размерами не выходящими за границу поля допуска, были бы признаны годными.

Распределение измеренных деталей графически можно изобразить в виде усеченной кривой распределения (заштрихованная площадь).

На рисунке показан характер искажения кривой распределения отклонений размеров деталей, измеренных с определенной погрешностью.

Для оценки влияния погрешности измерения на результаты разбраковки установлена связь между:

— погрешности измерения

— вероятностью неправильного принятия бракованных деталей m

— вероятностью забракования годных деталей n

— вероятностной величиной выхода размера за границу поля допуска c у неправильно принятых деталей

Значения m, n и c называются параметрами разбраковки.

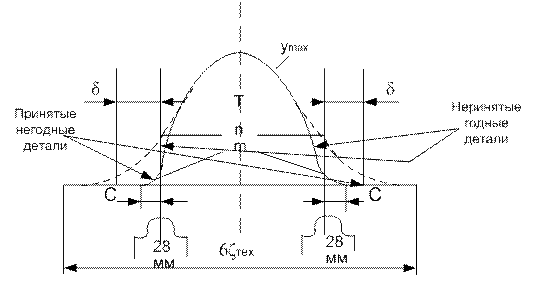
Для того чтобы деталь, имеющая отклонения размера, выходящие за границу поля допуска, была признана по результатам измерения годной, необходимо, чтобы в тот момент, когда контролируется деталь с отклонениями, выходящими за границу поля допуска на величину х, погрешность измерения проявилась с обратным знаком и величиной большей, чем это отклонение.

Разработаны графики по определению параметров разбраковки при распределении контролируемых размеров по нормальному закону.

Анализ полученных данных о параметрах разбраковки дает возможность установить ряд особенностей, имеющих практическое и теоретическое значение.

1. При уменьшении относительной точности изготовления возрастет число неправильно принятых и неправильно забракованных деталей.

2. Для распределения погрешностей изготовления размеров по нормальному закону и закону существенно-положительных величин графики параметров m и n имеют экстремальное значение.

3. На параметры разбраковки оказывают влияние точность технологического процесса изготовления в большей мере, чем погрешность измерения.

4. Соотношение между числом неправильно принятых и неправильно забракованных деталей не значительно меняется с изменением погрешности измерения. Более существенное влияние оказывает точность изготовления. Чем точнее технологический процесс, тем меньше неправильно принятых деталей по сравнению с неправильно забракованными.

5. При симметричных законах распределения погрешности измерения значения параметров разбраковки практически одинаковы для разных законов при равенстве .

6. Систематические погрешности измерения во многих случаях оказывают на параметры разбраковки большее влияние, чем случайные.

3. Допускаемая погрешность измерения.

Существуют нормативные документы по нормированию погрешности, допускаемой при измерении линейных размеров от 1 до 500 мм.

В этих документах устанавливаются:

1 – значения пределов допускаемых погрешностей измерения;

2 – приемочные границы с учетом нормируемых пределов допускаемых погрешностей измерения.

Значения пределов допускаемых погрешностей измерения

Приняты равными от 20% (для грубых допусков)

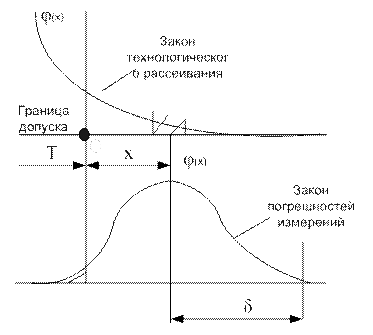
Нормируемая погрешность измерения относится к предельной погрешности, т.е. с учетом влияния всех составляющих погрешности измерения.

Допускаемая погрешность относится к случайным и неучтенным систематическим погрешностям измерения. Случайная погрешность принимается равной 2 .

Приведенные в нормативных документах допускаемые погрешности измерения являются наибольшими значениями, которые можно допустить при измерении. Меньше этих величин погрешности могут быть сколько угодно малыми, даже практически нулевыми, если это не вызывает дополнительных затрат по сравнению с измерением с допускаемой погрешностью.

Приемочные границы с учетом нормируемых пределов допускаемых погрешностей измерения

Приемочными границами называются значения размеров, по которым производится приемка изделий.

Они должны устанавливаться с учетом возможного влияния предельной допускаемой погрешности измерения.

Допуск на размер следует рассматривать как допуск на сумму погрешностей технологического процесса, которые не дают возможности получить абсолютно точное значение размера, в том числе из-за погрешности измерения.

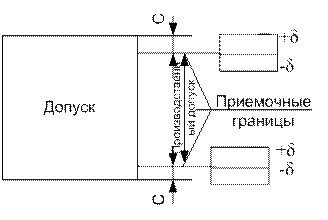
Для учета влияния погрешности измерения возможны 2 варианта.

При первом варианте приемочные границы устанавливают совпадающими с нормируемыми предельными значениями проверяемого изделия, т.е. возможное влияние погрешности измерения учитывается конструктором при выборе квалитета и вида посадок. Этот вариант можно считать основным, так как он принят в отечественной и зарубежной практике (без производственного допуска).

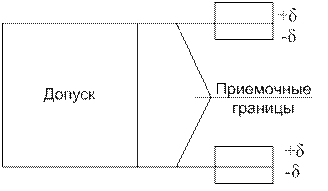
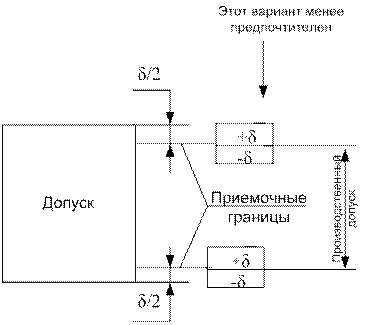
При втором варианте приемочные границы устанавливают с введением так называемого производственного допуска, т.е. нормируемые предельные значения размера смещают внутрь допуска с учетом возможного влияния погрешности измерения.

Смещение не должно превышать половины нормируемой допускаемой погрешности измерения. Этот вариант менее предпочтителен.

Рекомендуется при введении производственного допуска смещать приемочные границы на значение возможного выхода размера за границу поля допусков в зависимости от точности технологического процесса и погрешности измерения. Значения этих величин (вероятностный производственный допуск).

При нормировании допускаемой погрешности измерения устанавливаются требования к так называемой арбитражной препроверке, которая должна осуществляться с погрешностью измерения, не превышающей 30% предельной погрешности измерения, допускаемой при приемке.

При этом разрешается обнаружение среди годных определенного числа деталей, размеры которых выходят за границы поля допуска, но не более чем на половину значения допускаемых погрешностей измерения.

Методика выбора измерительных средств

В выборе измерительных средств должны участвовать: конструкторская, технологическая, метрологическая службы в пределах выполняемых ими служебных обязанностей.

Источник

Уроки математики и физики для школьников и родителей

понедельник, 28 октября 2019 г.

Урок 16. Абсолютная и относительная погрешность

Для подсчёта абсолютной погрешности необходимо из большего числа вычесть меньшее число.

В школе учится 374 ученика. Если округлить это число до 400 , то абсолютная погрешность измерения равна :

На предприятии 1284 рабочих и служащих. При округлении этого числа до 1300 абсолютная погрешность составляет

При округлении до 1280 абсолютная погрешность составляет

Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Но при выполнении различных измерений мы обычно представляем себе границы абсолютной погрешности и всегда можем сказать, какого определённого числа она не превосходит.

Торговые весы могут дать абсолютную погрешность, не превышающую 5 г, а аптекарские – не превышающую одной сотой грамма.

Длина рулона обоев составляет.

Границу абсолютной погрешности называют предельной абсолютной погрешностью .

Но абсолютная погрешность не даёт нам представление о качестве измерения, то есть о том, насколько тщательно это измерение выполнено. Чтобы понять эту мысль, достаточно разобраться в таком примере.

Допустим, что при измерении коридора длиной в 20 м мы допустили абсолютную погрешность всего только в 1 см. Теперь представим себе, что, измеряя корешок книги, имеющий 18 см длины, мы тоже допустили абсолютную погрешность в 1 см. Тогда понятно, что первое измерение нужно признать превосходным, но зато второе – совершенно неудовлетворительным. Это значит, что на 20 м ошибка в 1 см вполне допустима и неизбежна, но на 18 см такая ошибка является очень грубой.

Отсюда ясно, что для оценки качества измерения существенна не сама абсолютная погрешность, а та доля, какую она составляет от измеряемой величины. При измерении коридора длиной в 20 м погрешность в 1 см составляет

Делаем вывод, что измеряя корешок книги, имеющий 18 см длины и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении коридора длиной в 20 м, то это измерение можно считать максимально точным.

Если ошибка, возникающая при измерении линейкой или каким либо другим измерительным инструментом, значительно меньше, чем деления шкалы этой линейки, то в качестве абсолютной погрешности измерения обычно берут половину деления. Если деления на линейке нанесены достаточно точно, то ошибка при измерении близка к нулю.

Для измерения длины болта использованы метровая линейка с делениями 0,5 см и линейка с делениями 1 мм. В обоих случаях получен результат 3,5 см. Ясно, что в первом случае отклонение найденной длины 3,5 см от истинной, не должно по модулю превышать 0,5 см, во втором случае 0,1 см.

Если этот же результат получится при измерении штангенциркулем, то

Данный пример показывает зависимость абсолютной погрешности и границ, в которых находится точный результат, от точности измерительных приборов. В одном случае ∆ l = 0,5 и, следовательно,

Длина листа бумаги формата А4 равна (29,7 ± 0,1) см. А расстояние от Санкт-Петербурга до Москвы равно (650 ± 1) км. Абсолютная погрешность в первом случае не превосходит одного миллиметра, а во втором – одного километра. Необходимо сравнить точность этих измерений.

Если вы думаете, что длина листа измерена точнее потому, что величина абсолютной погрешности не превышает 1 мм, то вы ошибаетесь. Напрямую сравнить эти величины нельзя. Проведём некоторые рассуждения.

При измерении длины листа абсолютная погрешность не превышает 0,1 см на 29,7 см, то есть в процентном отношении это составляет

Когда мы измеряем расстояние от Санкт-Петербурга до Москвы, то абсолютная погрешность не превышает 1 км на 650 км, что в процентном соотношении составляет

Видим, что расстояние между городами измерено точнее, чем длинна листа формата А4.

Истинное значение измеряемой величины известно бывает лишь в очень редких случаях, а поэтому и действительная величина абсолютной погрешности почти никогда не может быть вычислена. На практике абсолютной погрешности недостаточно для точной оценки измерения. Поэтому на практике более важное значение имеет определение относительной погрешности измерения.

Абсолютная погрешность, как мы убедились, не даёт возможности судить о качестве измерения. Поэтому для оценки качества приближения вводится новое понятие – относительная погрешность. Относительная погрешность позволяет судить о качестве измерения.

Относительная погрешность – это частное от деления абсолютной погрешности на модуль приближённого значения измеряемой величины, выраженная в долях или процентах.

Округлим дробь 14,7 до целых и найдём относительную погрешность приближённого значения :

При измерении в (сантиметрах) толщины b стекла и длины l книжной полки получили следующие результаты :

l ≈ 100 с точностью до 0,1.

Абсолютная погрешность каждого из этих измерений не превосходит 0,1 . Однако 0,1 составляет существенную часть числа 0,4 и ничтожную часть числа 100 . Это показывает, что качество второго измерения намного выше, чем первого.

Если взять абсолютную погрешность в 1 см, при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10% и 0,1%. Для отрезка длиной в 10 см погрешность в 1 см очень велика, это ошибка в 10% . А для десятиметрового отрезка 1 см не имеет значения, эта ошибка всего в 0,1%.

Чем меньше относительная погрешность измерения, тем оно точнее.

Различают систематические и случайные погрешности.

Систематической погрешностью называют ту погрешность, которая остаётся неизменной при повторных измерениях.

Случайной погрешностью называют ту погрешность, которая возникает в результате воздействия на процесс измерения внешних факторов и может изменять своё значение.

В большинстве случаев невозможно узнать точное значение приближённого числа, а значит, и точную величину погрешности. Однако почти всегда можно установить, что погрешность (абсолютная или относительная) не превосходит некоторого числа.

Продавец взвешивает арбуз на чашечных весах. В наборе наименьшая гиря – 50 г. Взвешивание показало 3600 г. Это число – приближённое. Точный вес арбуза неизвестен. Но абсолютная погрешность не превышает 50 г. Относительная погрешность не превосходит

Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной погрешностью.

Число, заведомо превышающее относительную погрешность (или в худшем случае равное ей), называется предельной относительной погрешностью.

На практике относительную погрешность округляют до двух значащих цифр, выполняя округление с избытком, то есть, всегда увеличивая последнюю значащую цифру на единицу.

Для х = 1,7 ± 0,2 относительная погрешность измерений равна :

Здесь а = 17,9 см. Можно принять ∆ = 0,1 см, так как с точностью до 1 мм измерить карандаш нетрудно, а значительно уменьшить предельную погрешность не удастся (при навыке можно прочесть на хорошей линейке и 0,02 и даже 0,01 см, но у самого карандаша рёбра могут отличаться на большую величину ). Относительная погрешность равна

По условию, предельная относительная погрешность должна составлять 0,05% от 35 мм. Следовательно, предельная абсолютная погрешность равна

Можно воспользоваться формулой

Подставляя в формулу

Действия над приближёнными числами.

Сложение и вычитание приближённых чисел.

Абсолютная погрешность суммы двух величин равна сумме абсолютных погрешностей отдельных слагаемых.

Складываются приближённые числа

Пусть предельная погрешность первого есть 5 , а второго 1. Тогда предельная погрешность суммы равна

Так, если истинное значение первого есть 270 , а второго 33 , то приближённая сумма

Найти сумму приближённых чисел :

0,0909 + 0,0833 + 0,0769 + 0,0714 + 0,0667

+ 0,0625 + 0,0588 + 0,0556 + 0,0526.

Предельная погрешность каждого слагаемого

Предельная погрешность суммы :

При значительном числе слагаемых обычно происходит взаимная компенсация погрешностей, поэтому истинная погрешность суммы лишь в исключительных случаях совпадает с предельной погрешностью или близка к ней. Насколько редки эти случаи, видно из предыдущего примера, где 9 слагаемых. Истинная величина каждого из них может отличаться в пятом знаке от взятого приближённого значения на 1, 2, 3, 4 или даже на 5 единиц в ту и в другую сторону.

Например, первое слагаемое может быть больше своего истинного значения на 4 единицы пятого знака, второе – на две, третье – меньше истинного на одну единицу и так далее.

– когда истинная величина каждого слагаемого больше приближённой величины на 0,00005 ;

– когда истинная величина каждого слагаемого меньше приближённой величины на 0,00005 .

Значит, случаи, когда погрешность суммы совпадает с предельной, составляют только 0,0000002% всех возможных случаев.

Найти сумму точных чисел :

0,0909 + 0,0833 + 0,0769 + 0,0714 + 0,0667

+ 0,0625 + 0,0588 + 0,0556 + 0,0526.

Сложение даёт следующий результат – 0,6187.

Округлим их до тысячных и сложим :

0,091 + 0,083 + 0,077 + 0,071 + 0,067

+ 0,062 + 0,059 + 0,056 + 0,053 = 0,619.

Предельная погрешность суммы :

Приближённая сумма отличается от истинной на 0,0003 , то есть на треть единицы последнего знака приближённых чисел. Все три знака приближённой суммы верны, хотя теоретически последняя цифра могла быть грубо неверной.

Произведём в наших слагаемых округление до сотых. Теперь предельная погрешность суммы будет :

0,09 + 0,08 + 0,08 + 0,07 + 0,07

+ 0,06 + 0,06 + 0,06 + 0,05 = 0,62.

Истинная погрешность составляет только 0,0013 .

Предельная абсолютная погрешность разности двух величин равна сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого.

Пусть предельная погрешность приближённого уменьшаемого 85 равна 2 , а предельная погрешность вычитаемого 32 равна 3 . Предельная погрешность разности

В самом деле, истинное значение уменьшаемого и вычитаемого могут равняться

Тогда истинная разность есть

Она на 5 отличается от приближённой разности 53 .

Относительная погрешность суммы и разности.

Предельную относительную погрешность суммы и разности легко найти, вычислив сначала предельную абсолютную погрешность.

Предельная относительная погрешность суммы (но не разности!) лежит между наименьшей и наибольшей из относительных погрешностей слагаемых. Если все слагаемые имеют одну и ту же (или примерно одну и ту же) предельную относительную погрешность, то и сумма имеет ту же (или примерно ту же) предельную относительную погрешность. Другими словами, в этом случае точность суммы (в процентном выражении) не уступает точности слагаемых. При значительном же числе слагаемых сумма, как правило, гораздо точнее слагаемых.

Найти предельную абсолютную и предельную относительную погрешность суммы чисел :

В каждом слагаемом суммы

24,4 + 25,2 + 24,7 = 74,3

предельная относительная погрешность примерно одна и та же, а именно :

Такова же она и для суммы.

Здесь предельная абсолютная погрешность равна 0,15 , а относительная

0,15 : 74,3 ≈ 0,15 : 75 = 0,2%.

В противоположность сумме разность приближённых чисел может быть менее точной, чем уменьшаемое и вычитаемое. > особенно велика в том случае, когда уменьшаемое и вычитаемое мало отличаются друг от друга.

Относительные погрешности при сложении и вычитании складывать нельзя.

Умножение и деление приближённых чисел.

При делении и умножении чисел требуется сложить относительные погрешности.

Пусть перемножаются приближённые числа 50 и 20 , и пусть предельная относительная погрешность первого сомножителя есть 0,4%, а второго 0,5%.

Тогда предельная относительная погрешность произведения

приближённо равна 0,9% . В самом деле предельная абсолютная погрешность первого сомножителя есть

Поэтому истинная величина произведения не больше чем

(50 + 0,2)(20 + 0,1) = 1009,02,

Если истинная величина произведения есть 1009,2 , то погрешность произведения равна

а если 991,02 , то погрешность произведения равна

Рассмотренные два случая – самые неблагоприятные. Значит, предельная абсолютная погрешность произведения есть 9,02 . Предельная относительная погрешность равна

Источник