Что называется поверхностью вращения приведите примеры

10.04.202214.04.2022 admin 0 Comments

Поверхность вращения.

Поверхностью вращения называется такая поверхность, которая формируется в результате вращения некоторой не изменяющейся линии (MN), ее принято обозначать как образующую, вокруг неподвижной прямой (AB), обозначаемой как ось.

При этом примем, что образующая (MN), при своем вращении линия, обязательно взаимосвязана с осью (AB).

Отметим на образующей произвольную точку P и прочертим из нее на ось перпендикуляр PO. При вращении остается без изменений длина этого перпендикуляра, величина угла AOP и местоположение точки O.

Вследствие чего любая точка образующей описывает окружность, плоскость которой перпендикулярна к оси и центр располагается на пересечении этой плоскости с осью.

Отсюда можно сделать вывод, что плоскость, перпендикулярная к оси, пересекаясь с поверхностью вращения, формирует в сечении окружность.

Значит поверхность вращения – это просто граница тела вращения. Ведь поверхность это всегда граница тела.

Источник

Поверхности вращения в начертательной геометрии с примерами

Содержание:

Поверхностей вращения существует множество: цилиндр, конус, сфера, эллипсоиды, торы и др. Поверхность вращения общего вида образуется вращательным перемещением образующей линии вокруг неподвижной оси. Каждая точка образующей линии при вращении вокруг неподвижной оси описывает окружность с центром на оси вращения. Эти окружности называются параллелями.

Поверхности вращения

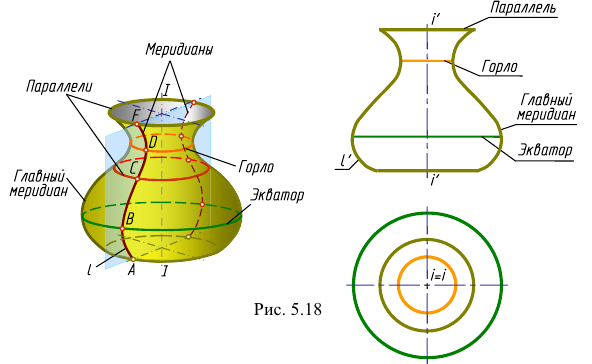
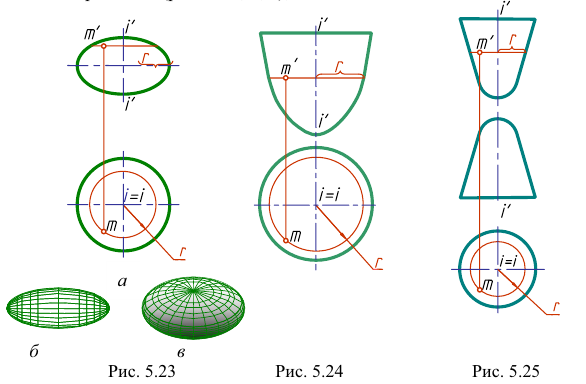
Поверхностью вращения называется поверхность, описываемая кривой (или прямой) образующей при ее вращении вокруг неподвижной оси (рис. 5.18). Эта поверхность определяется на чертеже заданием образующей и оси вращения.

Каждая точка образующей

На чертеже ось вращения располагают перпендикулярно к одной из плоскостей проекций, например горизонтальной. Тогда все параллели проецируются на эту плоскость в истинную величину. Экватор и горло определят горизонтальный очерк поверхности. Фронтальным очерком такой поверхности будет главный меридиан, то есть меридиан, расположенный во фронтальной плоскости.

Рассмотрим некоторые тела и поверхности вращения.

Точка А, лежащая на перпендикуляре к оси вращения и образующей, будет описывать наименьшую окружность, являющуюся горлом гиперболоида. Однополостный гиперболоид может быть также получен вращением гиперболы вокруг ее мнимой оси.

3. Поверхности вращения, образованные вращением кривых второго порядка:

Пересечение поверхностей вращения плоскостью

Развертки поверхностей вращения

Построение разверток поверхностей вращения имеет большое значение, особенно при конструировании из листового материала моделей различных сооружений, форм для металлических отливок, сосудов, трубопроводов, резервуаров и т.п.

Приближенные развертки

Поверхности, которые можно совместить с плоскостью без разрывов и складок, называют развертывающимися поверхностями. Фигуру, полученную при совмещении развертывающейся поверхности с плоскостью, называют разверткой. Для развертывающихся поверхностей можно построить приближенную развертку (условно-развертываемые поверхности). При построении приближенной развертки поверхность аппроксимируют поверхностями вписанных или описанных многогранников, имеющих грани в форме прямоугольников или треугольников. Поэтому при графическом выполнении разверток поверхности всегда приходится производить разгибание или спрямление кривых линий, принадлежащих поверхности, что неизбежно приводит к потере точности.

Условные развертки

Неразвертывающиеся поверхности не могут быть совмещены сплоскостью без разрывов и складок, т.е. теоретически они не имеют своей развертки. Поэтому говорят лишь об условном решении задачи по построению разверток неразвертывающихся поверхностей. На практике для получения развертки неразвертываемой поверхности, выполненной из листового материала, приходится кроме изгибания производить растяжение и сжатие определенных участков листа.

Построение условной развертки неразвертывающейся поверхности состоит в том, что отсеки заданной поверхности аппроксимируются отсеками развертывающихся поверхностей — гранными, цилиндрическими или коническими.

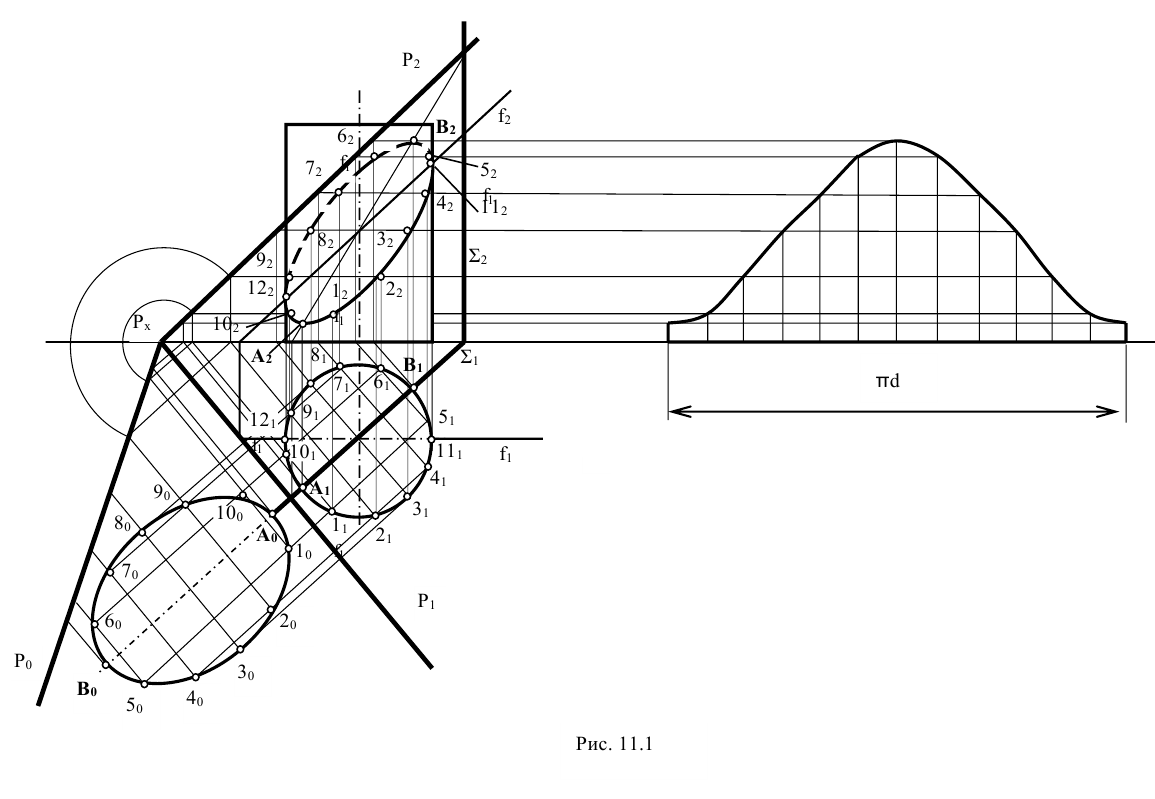
Задание: построить проекции и натуральный вид фигуры сечения поверхности цилиндра плоскостью Р (рис. 11.1). Построить развёртку боковой поверхности усечённой части цилиндра.

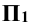
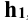
Решение: на рисунке 11.1 изображены прямой круговой цилиндр, основание которого принадлежит горизонтальной плоскости проекций и секущая плоскость Р общего положения. Поскольку секущая плоскость наклонена к оси цилиндра, то боковая поверхность цилиндра пересекается по эллиптической кривой.Форма сечения в этом случае зависит от того, пересекает ли плоскость Р основания цилиндра. В рассматриваемом случае секущая плоскость Р не пересекает оснований цилиндра. Это видно из того, что горизонтальная проекция нижнего основания не пересекается с горизонтальным следом плоскости Р, а горизонтальная проекция горизонтали , по которой плоскость Р пересекается с плоскостью верхнего основания, не пересекает его горизонтальную проекцию.

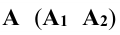
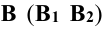
Для нахождения эллипса сечения плоскости Р с боковой поверхностью цилиндра находят сначала его низшую и высшую точки.

Эти точки являются концами большой оси эллипса сечения и лежат на линии наибольшего наклона плоскости Р к горизонтальной плоскости проекций. Следовательно, прямая АВ перпендикулярна к горизонтальному следу плоскости Р и пересекает ось цилиндра.

Для нахождения точек А и В проводят плоскость Σ, перпендикулярную к горизонтальному следу и проходящую через ось цилиндра. Эта плоскость перпендикулярна к плоскости . Затем находят линию пересечения плоскостей Р и Σ.

Боковая поверхность цилиндра является горизонтально проецирующей и поэтому проецируется на горизонтальную плоскость проекций в окружность. Так как отрезок АВ является частью линии пересечения плоскостей Р и Σ, а точки А и В лежат на боковой поверхности цилиндра, то горизонтальные проекции точек А и В должны лежать на одной окружности и на горизонтальной проекции прямой пересечения плоскостей Р и Σ. По горизонтальным проекциям точек А и В находят их фронтальные проекции, исходя из условия, что точки А и В лежат на найденной прямой пересечения плоскостей Р и Σ.

Для определения остальных точек эллипса сечения на цилиндрической поверхности выбирают ряд образующих. За первую образующую выбирают ту, на которой лежит точка А. Остальные образующие получают делением окружности (горизонтальной плоскости цилиндрической поверхности) на 12 равных частей (можно делить на другое количество частей). Затем находят точки пересечения образующих с плоскостью Р. В рассматриваемом примере все образующие перпендикулярны к горизонтальной плоскости проекций. Следовательно, горизонтальные проекции точек пересечения образующих с плоскостью Р совпадают с горизонтальными проекциями самих образующих.

Далее наносят горизонтальные проекции точек пересечения образующих с плоскостью Р (1, 2, 3, 4, 5, 6, 7, 8, 9, 10) и находят фронтальные проекции этих точек, проводя через них горизонтали в плоскости.

Развёртка боковой поверхности прямого кругового цилиндра, не усечённого плоскостью, представляет собой прямоугольник с основанием, равным длине окружности основания цилиндра, и высотой, равной высоте цилиндра. При построении развёртки боковой поверхности цилиндра, пересечённого плоскостью, на развёртке необходимо наносить точки, принадлежащие линии пересечения, и затем эти точки соединять плавной кривой линией (рис. 11.1).

Для этого на развёртке боковой поверхности цилиндра проводят 12 образующих, отстоящих друг от друга на равном расстоянии. За первую образующую рекомендуется выбирать ту, на которой лежит точка А. Затем наносят на все образующие последовательно точки А, 1, 2, 3, 4, 11, 5, В, 6, 7, 8, 9, 12, 10. Расстояние от этих точек до нижнего (или верхнего) основания проецируется на фронтальную плоскость проекций в натуральную величину. Соединив полученные точки плавной кривой линией, получают развёртку боковой поверхности усечённой части цилиндра.

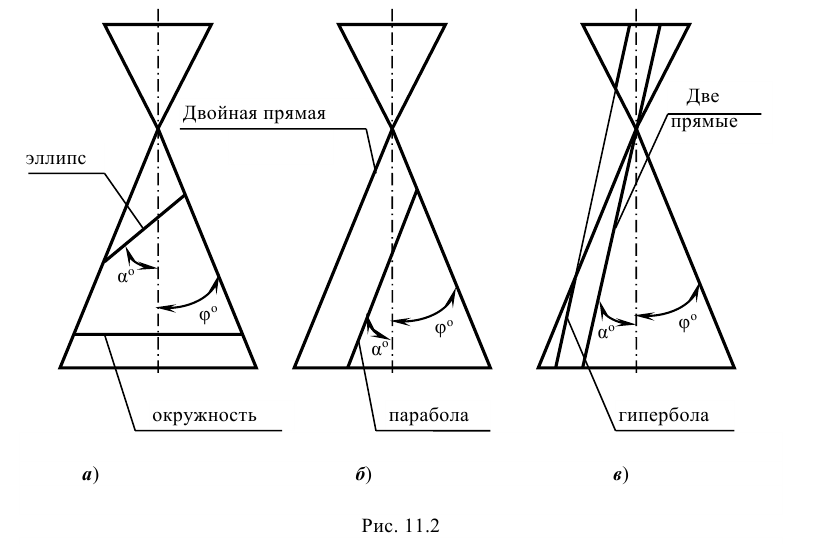
Задание: построить проекции и натуральную величину линии пересечения поверхности конуса плоскостью Р (рис. 11.3).

Решение: поверхность прямого кругового конуса относится к поверхностям вращения и является носителем кривых второго порядка: окружности, эллипса, параболы и гиперболы. Все эти кривые являются плоскими и, следовательно, могут быть получены в результате сечения конической поверхности плоскостью.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Что называется поверхностью вращения приведите примеры

Геометрическая часть определителя состоит из двух линий: образующей m и оси i (рис 96.б).

Алгоритмическая часть включает две операции:

1. на образующей m выделяют ряд точек A, B, C, … F,

2. каждую точку вращают вокруг оси i.

Рисунок 96. Образование поверхности вращения

Так создается каркас поверхности, состоящей из множества окружностей (рис.97), плоскости которых расположены перпендикулярно оси i. Эти окружности называются параллелями ; наименьшая параллель называется горлом , наибольшая – экватором .

Из закона образования поверхности вращения вытекают два основных свойства:

1. Плоскость перпендикулярная оси вращения, пересекает поверхность по окружности – параллели .

2. Плоскость, проходящая через ось вращения, пересекает поверхность по двум

симметричным относительно оси линиям – меридианам .

Плоскость, проходящая через ось параллельно фронтальной плоскости проекций называется плоскостью главного меридиана , а линия, полученная в сечении, – главным меридианом .

Рисунок 97. Поверхность вращения

Рассмотрим наиболее распространенные поверхности вращения с криволинейными образующими:

Сфера – образуется вращением окружности вокруг её диаметра (рис.98).

При сжатии или растяжении сферы она преобразуется в эллипсоиды , которые могут быть получены вращением эллипса вокруг одной из осей: если вращение вокруг малой оси, то эллипсоид называется сжатым или сфероидом (рис.99), если вокруг большой – вытянутым (рис.100).

Рисунок 98. Образование сферы

Рисунок 99. Образование сфероида

Тор – образуется при вращении окружности вокруг оси, не проходящей через центр окружности (рис.101).

Рисунок 100. Образование вытянутого
эллипсоида

Параболоид вращения – образуется при вращении параболы вокруг своей оси (рис.102).

Рисунок 102. Параболоид вращения

Гиперболоид вращения – различают одно (рис.103а) и двух (рис.103б) полостной гиперболоиды вращения. Первый получается при вращении вокруг мнимой оси, а второй – вращением гиперболы вокруг действительной оси.

Источник

Поверхности вращения

Поверхностью вращения называется поверхность, образованная вращением образующей вокруг неподвижной оси (рис. 1). Эта поверхность определяется на чертеже заданием образующей и оси вращения.

Каждая точка образующей I описывает при своем вращении окружность, лежащую в плоскости, перпендикулярной оси вращения, с центром на оси. Эти окружности называются параллелями. Наибольшая из этих параллелей называется экватором, наименьшая — горлом.

Плоскость, проходящую через ось поверхности вращения, называют меридианальной. Линию ее пересечения с поверхностью — меридианом. Меридиан, параллельный фронтальной плоскости проекций, называется главным меридианом. Все меридианы равны между собой.

На чертеже ось вращения II располагают перпендикулярно к одной из плоскостей проекций, например горизонтальной. Тогда все параллели проецируются на эту плоскость в истинную величину. Экватор и горло определят горизонтальный очерк поверхности. Фронтальным очерком такой поверхности будет главный меридиан, то есть меридиан, расположенный во фронтальной плоскости.

Точки на поверхностях вращения могут быть построены с помощью параллелей, то есть окружностей на поверхности.

Цилиндром вращения называется поверхность, образованная вращением прямой вокруг параллельной ей оси.

Если ось цилиндра перпендикулярна горизонтальной плоскости проекций, то горизонтальные проекции точек, лежащих на его поверхности, будут расположены на окружности, в которую спроецируется цилиндр на горизонтальную плоскость Н (рис. 2).

Задача. Найти недостающие проекции точек М и К (рис. 2)

Для того, чтобы найти горизонтальную проекцию точки М, проведем линию связи от фронтальной проекции М(m’) до пересечения с горизонтальной проекцией цилиндра (окружностью). Задача имеет два ответа: точки m1 и m2.

Однозначно определить положение фронтальной проекции точки К по одной только горизонтальной проекции k невозможно. По линии связи, проведенной от горизонтальной проекции этой точки, на поверхности цилиндра может находиться бесчисленное множество точек. В этом случае необходима дополнительная информация о положении точки К.

При пересечении цилиндра вращения плоскостью, параллельной оси вращения, в сечении получаются две прямые — образующие (рис. 3).

Если секущая плоскость перпендикулярна оси вращения, в результате сечения получится окружность (рис. 4).

В общем случае, когда секущая плоскость наклонена к оси вращения цилиндра, в сечении получается эллипс (рис. 5).

Сечение цилиндра плоскостью

В общем случае построение линии пересечения поверхности плоскостью заключается в нахождении общих точек, то есть точек, принадлежащих одновременно секущей плоскости и поверхности.
Для нахождения этих точек применяют способ дополнительных секущих плоскостей:

Дополнительные плоскости проводят таким образом, чтобы они пересекали поверхность по наиболее простым линиям.

Нахождение точек линии пересечения начинают с определения характерных (опорных) точек. К ним относятся

Для более точного построения линии пересечения необходимо построить еще и дополнительные (промежуточные) точки.

Прямой круговой конус

Сечение конуса плоскостью

В зависимости от направления секущей плоскости в сечении конуса вращения могут получиться различные линии.

Если секущая плоскость наклонена к оси вращения конуса и не проходит через его вершину, в сечении конуса могут получиться эллипс, парабола или гипербола (рис. 8, в, г, д) — в зависимости от величины угла наклона секущей плоскости.

Для конуса наиболее простыми линиями являются прямые (образующие) и окружности.

Горизонтальную проекцию точки А найдем с помощью образующей. Проведем через точку А и вершину конуса S вспомогательную фронтально-проецирующую плоскость Р(Рv). Она пересекает конус по двум образующим SM и SN. Их фронтальные проекции совпадают. Строим горизонтальные проекции образующих. Затем проводим через точку а’ линию связи. На пересечении линии связи и горизонтальных проекций образующих определим горизонтальную проекцию точки. Задача имеет два ответа: точки а₁ и а₂ (рис. 9).

Горизонтальную проекцию точки В найдем, построив окружность, на которой она лежит. Для этого через точку проведем горизонтальную плоскость Т(Тv), которая пересекает конус по окружности радиуса r.

Строим горизонтальную проекцию этой окружности. Через точку b’ проведем линию связи до ее пересечения с окружностью. Задача также имеет два ответа — точки b₁ и b₂.

Рассмотрим пример построения проекций линии пересечения конуса фронтально — проецирующей плоскостью Р (P_V). В этом случае в сечении получается эллипс (рис. 10).

Сначала определим характерные (опорные) точки.

Фронтальная проекция линии сечения совпадает с фронтальным следом плоскости P_V. Нижняя точка 1 лежит на образующей AS, верхняя — 2 на образующей ВS. Эти точки определяют положение большой оси эллипса. Малая ось эллипса перпендикулярна большой оси.

Чтобы найти малую ось, разделим отрезок 1-2 на две равные части. Точки 3 и 4 определяют малую ось эллипса. Точки 5 и 6, расположенные на образующих CS и DS, являются точками границы видимости для профильной плоскости проекций. Проекции точек 1, 2, 5 и 6 находятся на соответствующих проекциях образующих. Чтобы найти проекции точек 3 и 4, проводим дополнительную секущую плоскость Т(Тv).

Она рассекает конус по окружности радиуса г. На этой окружности находятся проекции данных точек. Для точного построения необходимо определить дополнительные (случайные точки). Проекции этих точек находим аналогично точкам 3 и 4 или проводя через эти точки образующие. Соединяем полученные проекции точек. Определяем видимость. На горизонтальной плоскости все точки, лежащие на поверхности конуса, видимы. На профильной — точки 5, 3, 1, 4, 6 видимы, остальные — нет.

Шаровой поверхностью (или сферой) называется поверхность, образованная при вращении окружности вокруг своего диаметра.

Если шаровая поверхность пересекается плоскостью, то в сечении всегда получается окружность, которая может спроецироваться:

Чтобы построить проекции точки, лежащей на поверхности шара, необходимо через нее провести секущую плоскость, параллельную плоскости проекций, затем построить окружность, на которой находится эта точка.

Сечение шаровой поверхности плоскостью

Пересечем поверхность шара фронтально-проецирующей плоскостью Q(Q_v) (рис. 12). Построение начинаем с определения характерных точек.

Точки 1 и 2 находятся на главном меридиане. Эти точки — концы малой оси эллипса, а также это самая высокая и самая низкая точки. Их горизонтальные и профильные проекции строим по фронтальным проекциям.

Точки 3 и 4 находятся на профильном меридиане и определяют видимость на профильной плоскости проекций. Горизонтальные проекции точек находим по профильным проекциям.

Точки 5 и 6 принадлежат экватору и являются точками границы видимости на горизонтальной проекции. Профильные проекции точек находим по горизонтальным проекциям.

Чтобы найти положение большой оси эллипса (точки 7 и 8) разделим отрезок 12 пополам. Фронтальные проекции точек (точки 7 и 8) совпадают с серединой этого отрезка. В этой же точке находится фронтальная проекция центра окружности сечения. На горизонтальную плоскость диаметр окружности проецируется без искажения. Поэтому точки 7 и 8 будут находиться на расстоянии R от центра окружности сечения (рис. 12).

Для большей точности строим несколько дополнительных точек.

Полученные точки соединяем плавной кривой линией с учетом ее видимости.

Тор — поверхность, полученная вращением окружности вокруг оси, лежащей в плоскости этой окружности, но не проходящей через ее центр.

Если ось вращения проходит вне окружности, то поверхность называется «открытый тор» или «тор — кольцо» (рис. 13); если ось касает тор» (рис. 15 — 16). Тор, изображенный на рис. 15, называется также «тор-яблоко», а на рис. 16 — «тор-лимон». Сфера — частный случай торовой поверхности.

рис. 13 рис. 14 рис. 15 рис. 16