Что называется показательной функцией

Лекция по математике на тему «Показательная функция»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Некоторые наиболее часто встречающиеся виды трансцендентных функций, прежде всего показательные, открывают доступ ко многим исследованиям.

«Показательная функция, её свойства и график».

() = , (5)

a x > 1, если a > 1, x > 0, (7)

Рассмотрим несколько примеров применения этих свойств.

Найдите значение выражения: 7 ·7·7— 5·5·5.

Показательная функция обладает следующими свойствами:

Область определения показательной функции – множество R всех действительных чисел.

Множество значений показательной функции – множество всех положительных чисел.

Показательная функция y = a x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 a

Это следует из свойств (8) и (9).

Построим графики функций y = 2 x и y = , используя рассмотренные свойства и построив несколько точек, принадлежащих графику.

y= x

8 8

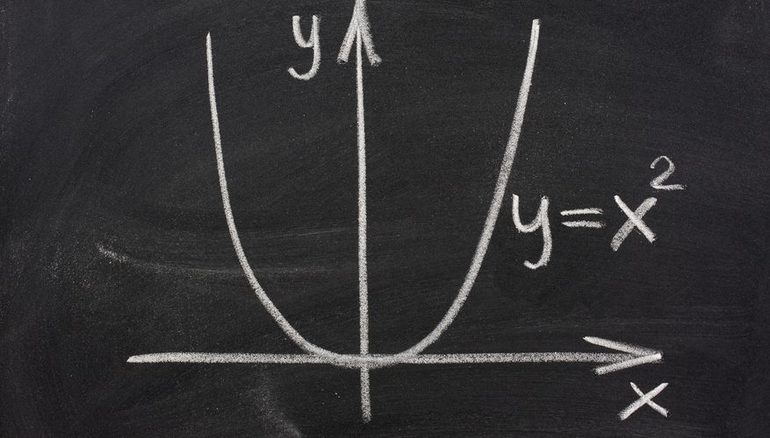
Отметим, что график функции y = 2 x проходит через точку (0;1) и расположен выше оси ох.

если x > 0 и увеличивается, то график быстро поднимается вверх.

Такой же вид имеет график любой функции y = а x , если a > 1.

График функции y = () X также проходит через точку (0;1) и расположен выше оси ох. Если x > 0 и увеличивается, то график быстро приближается к оси ох (не пересекая её); если x

Такой же вид имеет график любой функции

y = (а) X , если a

С помощью показательной функции выражается давление воздуха в зависимости от высоты подъёма, ток самоиндукции в катушке после включения постоянного напряжения и т.д.

Рассмотрим несколько примеров показательных уравнений , т.е. уравнений , в которых неизвестное содержится в показателе степени.

Простейшие показательные уравнения

Aa 2 x + Ba x + C = 0

подстановкой a x = y

сводится к квадратному

x = 2; функция не может

Решить графически уравнение:

Определение: неравенство, содержащее переменную в показателе степени называется показательным.

a f ( x ) a g ( x ) равносильно f ( x ) g ( x )

a f ( x ) a g ( x ) равносильно f ( x ) > g ( x )

Источник

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №21. Показательная функция.

Перечень вопросов, рассматриваемых в теме:

— какая функция называется показательной;

— какие свойства имеет показательная функция в зависимости от ее основания;

— какой вид имеет график показательной функции в зависимости от ее основания;

— примеры реальных процессов, описываемых показательной функцией.

Функция вида , a>0, а≠1 называется показательной функцией с основанием а.

Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб.для общеобразоват. учреждений: базовый и профил. уровни 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-025401-4, сс.310-314, сс. 210-216.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

1. Определение, свойства и график показательной функции

Такое название она получила потому, что независимая переменная стоит в показателе. Основание а – заданное число.

Для положительного основания значение степени а х можно найти для любого значения показателя х – и целого, и рационального, и иррационального, то есть для любого действительного значения.

Сформулируем основные свойства показательной функции.

1. Область определения.

Как мы уже сказали, степень а х для a>0 определена для любого действительного значения переменной х, поэтому область определения показательной функции D_(y)=R.

2. Множество значений.

Так как основание степени положительно, то очевидно, что функция может принимать только положительные значения.

3. Корни (нули) функции.

Так как основание a>0, то ни при каких значениях переменной х функция не обращается в 0 и корней не имеет.

При a>1 функция монотонно возрастает.

Рисунок 1 – График показательной функции при a>1

При 0 1 при х стремящемся к минус бесконечности.

2. Рассмотрим пример исследования функции y=–3 х +1.

1) Область определения функции – любое действительное число.

2) Найдем множество значений функции.

Так как 3 х >0, то –3 х х +1 х +1 представляет собой промежуток (-∞; 1).

3) Так как функция y=3 х монотонно возрастает, то функция y=–3 х монотонно убывает. Значит, и функция y=–3 х +1 также монотонно убывает.

4) Эта функция будет иметь корень: –3 х +1=0, 3 х =1, х=0.

Рисунок 3 – График функции y=–3 х +1

6) Для этой функции горизонтальной асимптотой будет прямая y=1.

3. Примеры процессов, которые описываются показательной функцией.

6) Известно утверждение, что количество информации удваивается каждые 10 лет. Изобразим это наглядно.

Примем количество информации в момент времени t=0 за единицу. Тогда через 10 лет количество информации удвоится и будет равно 2. Еще через 10 лет количество информации удвоится еще раз и станет равно 4 и т.д.

Рисунок 4 – График функции y=2 х – изменение количества информации

Примеры и разбор решения заданий тренировочного модуля

Выберите показательные функции, которые являются монотонно убывающими.

Монотонно убывающими являются показательные функции, основание которых положительно и меньше единицы. Такими функциями являются: 2) и 4) (независимо от того, что коэффициент в показателе функции 4) равен 0,5), заметим, что функцию 4) можно переписать в виде: , используя свойство степеней.

Также монотонно убывающей будет функция 5). Воспользуемся свойством степеней и представим ее в виде:

2) 4) 5)

Найдите множество значений функции y=3 x+1 – 3.

Так как 3 x+1 >0, то 3 x+1 – 3>–3, то есть множество значений:

Найдите множество значений функции y=|2 x – 2|

2 x –2>–2, но, так как мы рассматриваем модуль этого выражения, то получаем: |2 x – 2|0.

Источник

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №21. Показательная функция.

Перечень вопросов, рассматриваемых в теме:

— какая функция называется показательной;

— какие свойства имеет показательная функция в зависимости от ее основания;

— какой вид имеет график показательной функции в зависимости от ее основания;

— примеры реальных процессов, описываемых показательной функцией.

Функция вида , a>0, а≠1 называется показательной функцией с основанием а.

Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб.для общеобразоват. учреждений: базовый и профил. уровни 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-025401-4, сс.310-314, сс. 210-216.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

1. Определение, свойства и график показательной функции

Такое название она получила потому, что независимая переменная стоит в показателе. Основание а – заданное число.

Для положительного основания значение степени а х можно найти для любого значения показателя х – и целого, и рационального, и иррационального, то есть для любого действительного значения.

Сформулируем основные свойства показательной функции.

1. Область определения.

Как мы уже сказали, степень а х для a>0 определена для любого действительного значения переменной х, поэтому область определения показательной функции D_(y)=R.

2. Множество значений.

Так как основание степени положительно, то очевидно, что функция может принимать только положительные значения.

3. Корни (нули) функции.

Так как основание a>0, то ни при каких значениях переменной х функция не обращается в 0 и корней не имеет.

При a>1 функция монотонно возрастает.

Рисунок 1 – График показательной функции при a>1

При 0 1 при х стремящемся к минус бесконечности.

2. Рассмотрим пример исследования функции y=–3 х +1.

1) Область определения функции – любое действительное число.

2) Найдем множество значений функции.

Так как 3 х >0, то –3 х х +1 х +1 представляет собой промежуток (-∞; 1).

3) Так как функция y=3 х монотонно возрастает, то функция y=–3 х монотонно убывает. Значит, и функция y=–3 х +1 также монотонно убывает.

4) Эта функция будет иметь корень: –3 х +1=0, 3 х =1, х=0.

Рисунок 3 – График функции y=–3 х +1

6) Для этой функции горизонтальной асимптотой будет прямая y=1.

3. Примеры процессов, которые описываются показательной функцией.

6) Известно утверждение, что количество информации удваивается каждые 10 лет. Изобразим это наглядно.

Примем количество информации в момент времени t=0 за единицу. Тогда через 10 лет количество информации удвоится и будет равно 2. Еще через 10 лет количество информации удвоится еще раз и станет равно 4 и т.д.

Рисунок 4 – График функции y=2 х – изменение количества информации

Примеры и разбор решения заданий тренировочного модуля

Выберите показательные функции, которые являются монотонно убывающими.

Монотонно убывающими являются показательные функции, основание которых положительно и меньше единицы. Такими функциями являются: 2) и 4) (независимо от того, что коэффициент в показателе функции 4) равен 0,5), заметим, что функцию 4) можно переписать в виде: , используя свойство степеней.

Также монотонно убывающей будет функция 5). Воспользуемся свойством степеней и представим ее в виде:

2) 4) 5)

Найдите множество значений функции y=3 x+1 – 3.

Так как 3 x+1 >0, то 3 x+1 – 3>–3, то есть множество значений:

Найдите множество значений функции y=|2 x – 2|

2 x –2>–2, но, так как мы рассматриваем модуль этого выражения, то получаем: |2 x – 2|0.

Источник

Общие сведения

Функцией называется закон зависимости одной величины от другой. Выражается она при помощи выражений алгебраического, тригонометрического, иррационального и других типов. Существует два типа переменных, которые встречаются в любых функциях: зависимая и независимая. Последняя называется также аргументом.

Основной особенностью показательной функции считается ее вид, поскольку основанием является число, а степенью — аргумент. Последним называется независимая переменная, которая может принимать любые значения, кроме превращающих ее значение в пустое множество или неопределенность. Показательной называется функция вида z (y) = a^y (a > 0), которая зависит от аргумента в виде показателя степени «y».

Сферы использования

Применяется в описании различных законов роста какой-либо величины. В зависимости от показателя, функция может быстро возрастать. Иногда вместо основания «а» может быть указан символ экспоненты, которая стремительно возрастает. Пример показательной функции mc (t) = m0 * (½)^(t/T) используется при подсчете энергии, выделяемой во время деления ядер радиоактивного элемента за время t. Переменные и коэффициенты расшифровываются следующим образом:

Используя формулу геометрической прогрессии Sn = b1 * [(q^n) — 1] / (q — 1), можно без проблем вычислить значение. Первое значение b1 = 1, знаменатель q = 2 3 / 2 2 = 2 2 / 2 = 2 / 1 = 2. Общее число зерен определяется таким образом: S64 = 1 * [(2 64 ) — 1] / (2 — 1) = (2 64 ) — 1. Ученые подсчитали, что такое количество превышает урожай пшеницы на планете за 2008−2009 год в 1800 раз. Если воспользоваться справочником или компьютером, то S64 = 18446744073709551615 — 1 = 18446744073709551614.

Примеры иллюстрируют применение степенной функции в жизни, поскольку она может описывать явления природы, в которой протекают различные процессы. Например, деление клеток злокачественных опухолей, увеличение количества молекул озона при разрядах молнии и так далее.

Представление функции

Математики рекомендуют ознакомиться на начальных этапах с графиком показательной функции и ее свойствами. Графиком называется ее графическое представление в некоторой системе координат. В качестве последней распространена декартовая прямоугольная с двумя осями (ординат — z и абсцисс — y). Оси можно обозначать любыми литерами. Например, в формуле mc (t) = m0 * (½)^(t/T) рекомендуется использовать в качестве ординаты ось «mc», а абсциссой будет время t.

Необходимо рассмотреть свойства функции, а затем строить ее график. Они различаются между собой, поскольку существует несколько вариантов представления. Для правильного построения и анализа необходимо разобрать все варианты. Это позволит воспользоваться уже готовым материалом и существенно оптимизирует процесс решения задач. Представление функции состоит из свойств и графика.

Основные свойства

Свойствами функции z = a^y называется совокупность некоторых характеристик, присущих только ей. Они нужны не только для построения графика, но и для дифференцирования, анализа и интегрирования. Список свойств и полезных соотношений:

Свойства функции доказываются математическим путем. Они основаны на алгоритмах исследования ее поведения.

Доказательства некоторых утверждений

Соотношения необходимы для решения различных задач, основанных на дифференцировании, интегрировании и упрощении выражений. Можно доказать третье свойство, то есть попытаться найти минимум и максимум. Для нахождения экстремумов следует воспользоваться таким алгоритмом:

Точка пересечения с осью ординат рассчитывается таким образом: решается уравнение z = a^y относительно y, принимающего нулевое значение: z = a 0 = 1. Искомая точка имеет координаты (0;1).

Построение графиков

Для построения графика существуют свои правила, которых рекомендуют придерживаться математики. Процедура осуществляется в двух режимах: схематическом и точном. В первом случае нужно знать свойства. Таблица зависимостей значения от аргумента не составляется. При точном построении необходимо составить таблицу. В ней необходимо рассмотреть около 5-10 значений независимой переменной. Затем все точки отмечаются на декартовой системе координат и плавно соединяются.

Оформление играет очень важную роль, поскольку не допускаются исправления. Очень важно соблюдать масштаб, и не отмечать каждое значение шкалы делений на оси абсцисс и ординат. Следует учитывать, что графики чертят также в двух режимах: автоматизированном и ручном. В первом случае применяются специализированные программы и веб-приложения (онлайн-калькуляторы). В последнем необходимо чертить карандашом, используя линейку. Этот момент очень важен, поскольку приучает к дисциплине на уроках, а также повышает читабельность материала. Для примера нужно начертить график z = 2^y. Необходимо составить таблицу 1:

Таблица 1. Зависимость значения от аргумента (z = 2^y).

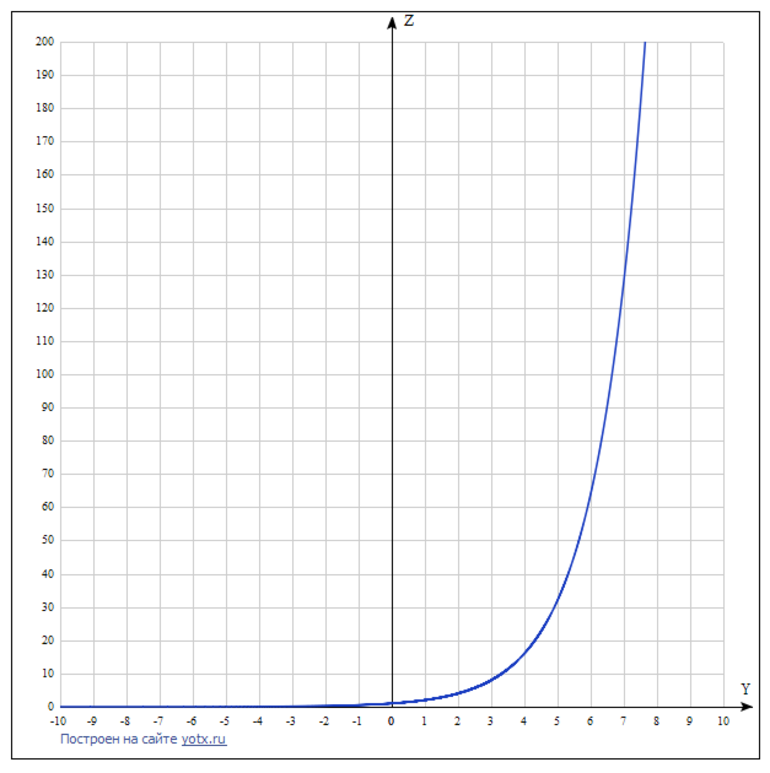
По таблице нужно построить график, отмечая координаты каждой из точек. После этого нужно плавно их соединить. Должен получиться примерно такой график:

Рисунок 1. График z = 2^y (a > 0 и y > 0).

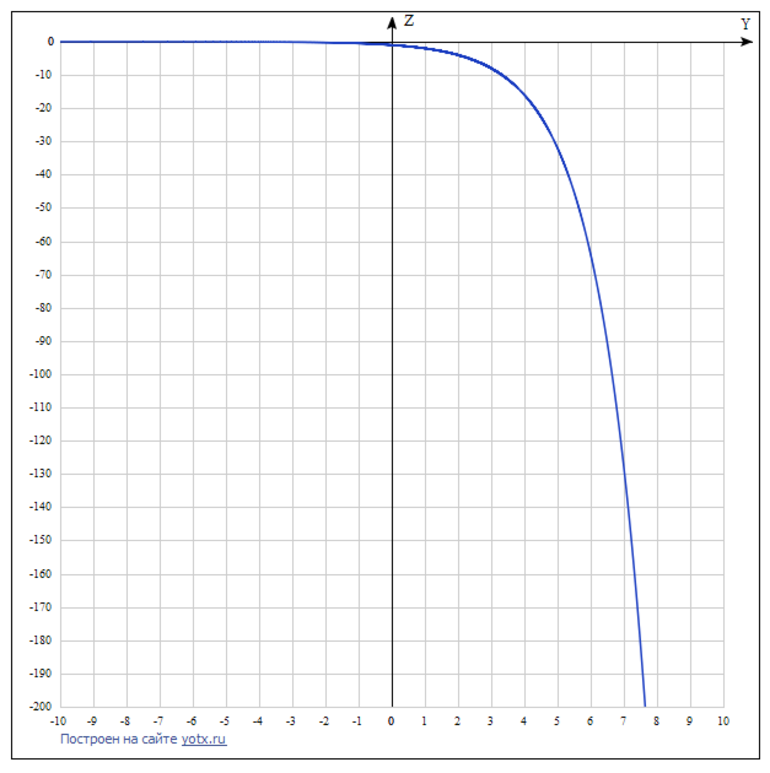
Если рассмотреть пример, в котором y > 0 и 0 0 график также существенно изменится, поскольку будет постоянно убывать:

Рисунок 3. Графическая иллюстрация при a 0.

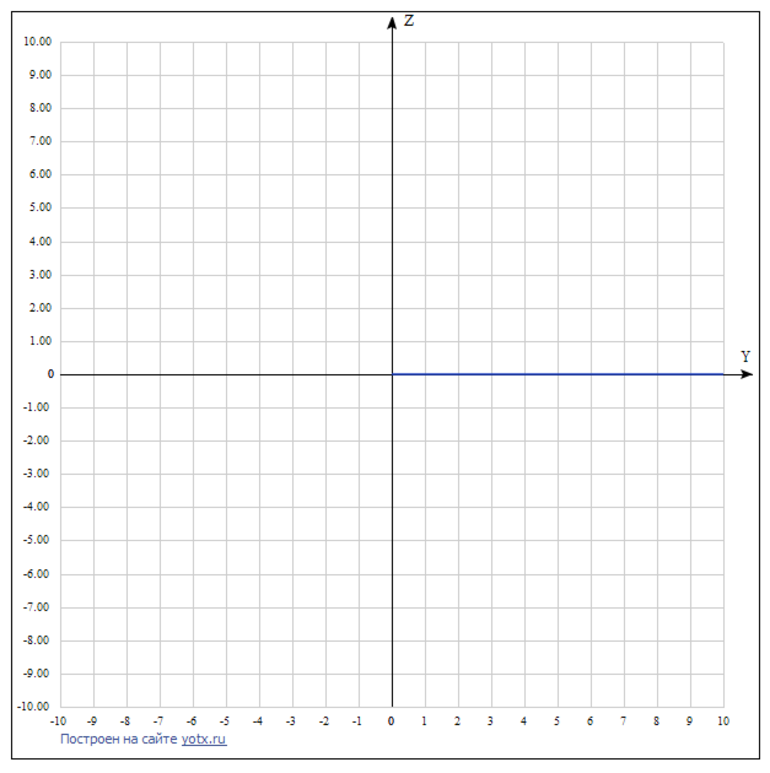
Когда основание равно 0, тогда функция перестает быть показательной, поскольку не соблюдается условие из определения. На рисунке 4 представлен ее график:

Рисунок 4. Графическое представление при a = 0 и x > 0.

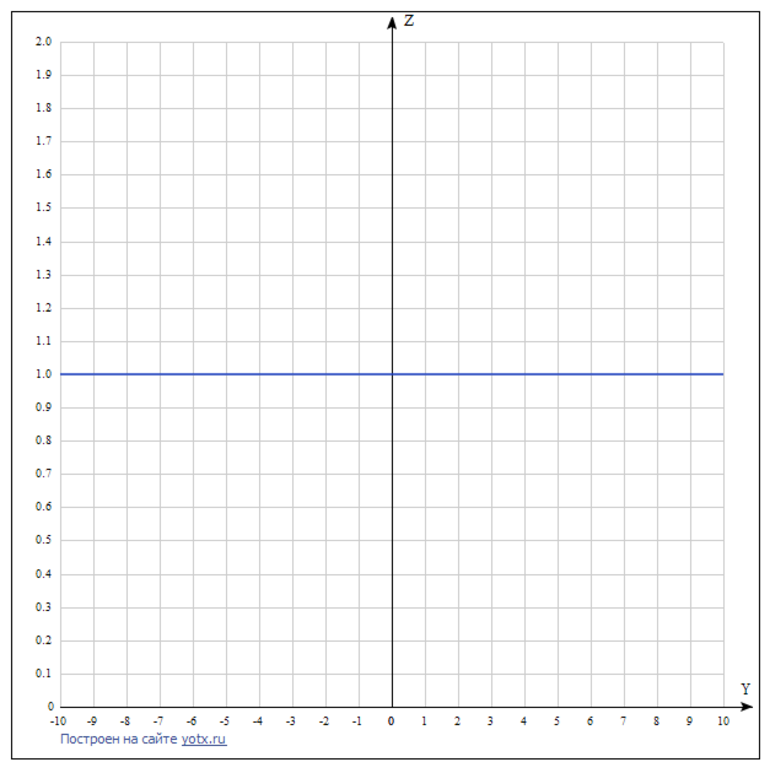
Последний случай — основание равно 1. Функция также не является показательной.

Рисунок 5. График при a = 1 и x > 0.

Кроме того, встречаются задачи не только на построение графика, но и на осуществление операций дифференцирования, нахождения производной и первообразной.

Правила дифференцирования

В некоторых задачах следует найти производную или дифференциал степенной функции. Для осуществления этой операции существует определенный алгоритм, который специалисты рекомендуют рассмотреть на конкретном примере. Условие задачи следующее: найти дифференциал z = 4^(6y). Для его нахождения нужно предпринять такие шаги:

Необходимо отметить, что производная берется из таблицы простейших (элементарных) функций. Когда выражение является сложным, как в примере, то дифференциал ищется по частям. Формула для сложного выражения имеет такой вид: [w(y(z(x)))]’ = [z(x)]’ * [y(z(x))]’ * [w(y(z(x)))]’. Соотношение трудно понять, но на примере все довольно просто. Например, нужно найти производную z = e^(2cos(2x^2 + 1)). Функция состоит из трех элементов: f = 2x^2 + 1, y = 2cos(f) и v = e^y.

Поиск первообразных

Отдельным классом задач является интегрирование или нахождение первообразных. Для этой цели применяются специальные таблицы интегралов простейших функций. Кроме того, можно воспользоваться и табличными значениями производных. Они позволяют найти искомое первообразное выражение. Интегрирование считается обратной операцией и позволяет найти тождество, из которого была получена производная.

Для нахождения интеграла a^y следует воспользоваться такой формулой: ∫(a^y)dy = ∫(e^(ln(a * y))dy = [1 / ln(a)] * ∫(e^(ln(a * y))d(ln(a * y) = [1 / ln(a)] * (e^(ln(a * y)) + C = [1 / ln(a)] * (a^y) + C. Коэффициент «С» — константа, которая при дифференцировании исчезает. Однако ее необходимо учитывать. Кроме того, необходимо постоянно следить за знаком интеграла и переменной, по которой находится первообразная.

Таким образом, для решения задач со степенной функцией нужно пользоваться свойствами и алгоритмами, поскольку это существенно сэкономит время и избавит от множества ошибок.

Источник