Что называется подмножеством множества
Множества
Множество — это совокупность любых объектов. Множества обозначают большими буквами латинского алфавита — от A до Z.
Основные числовые множества: множество натуральных чисел и множество целых чисел, всегда обозначаются одними и теми же буквами:
N — множество натуральных чисел,
Z — множество целых чисел.
Множества делятся на конечные и бесконечные. Конечное множество — множество, содержащее определённое (конечное) количество элементов. Бесконечное множество — множество, содержащее бесконечно много элементов. К бесконечным множествам можно отнести множества натуральных и целых чисел.
Для определения множества используются фигурные скобки, в которых через запятую перечисляются элементы. Например, запись
означает, что множество L состоит из четырёх чётных чисел.
Термин множество употребляется независимо от того, сколько элементов оно содержит. Множества не содержащие ни одного элемента называются пустыми.
Подмножество
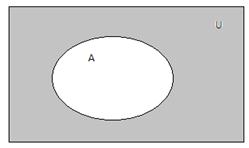
Подмножество — это множество, все элементы которого, являются частью другого множества.
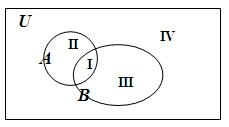
Визуально продемонстрировать отношение множества и входящего в него подмножества можно с помощью кругов Эйлера. Круги Эйлера — это геометрические схемы, помогающие визуализировать отношения различных объектов, в нашем случае, множеств.
Рассмотрим два множества:
Каждый элемент множества L принадлежит и множеству M, значит, множество L является подмножеством множества M. Такое соотношение множеств обозначают знаком ⊂ :
Рассмотрим два множества:
Так как оба множества состоят из одних и тех же элементов, то L = M.
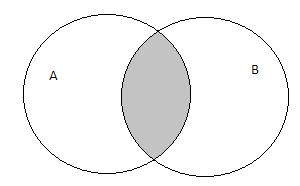
Пересечение и объединение множеств
Из данного примера следует, что пересечением множеств называется множество, которое содержит только те элементы, которые встречаются во всех пересекающихся множествах.
При объединении равных множеств объединение будет равно любому из данных множеств:
Множество и его элементы. Подмножества
Понятие множества
Что такое «множество», мы понимаем интуитивно. В этом смысле это понятие первично, так же как «точка» или «плоскость».
Создатель теории множеств Г.Кантор описывал множество как «многое, мыслимое нами как единое».
Приведём примеры множеств:
Множество людей в салоне самолёта
Множество деревьев в парке
Множество планет Солнечной системы
Множество электронов в атоме
Множество натуральных чисел
Множество «синих-синих презелёных красных шаров»
Конечное, бесконечное и пустое множества
Людей в салоне самолёта легко посчитать, это множество конечно.
С деревьями в парке, планетами и электронами – сложней. Скорее всего, мы не сможем назвать точное количество элементов этих множеств в данный момент времени. Однако, и эти множества конечны.
Натуральное число – это идеальный объект, абстракция. Множество натуральных чисел бесконечно. Как оказалось, человек может оперировать и абстракциями, и бесконечностями.
Можно себе представить даже то, «чего на свете вообще не может быть». Поскольку таких объектов нет, их множество будет пустым. Пустое множество является частью любого другого множества.
Помидоры на грядке
Числа (натуральные, рациональные, действительные и т.д.)
Количество рациональных чисел на отрезке [0;1]
Полосатые летающие слоны
Все точки пересечения двух параллельных прямых на плоскости
Способы задания множеств
1) Перечисление – в списке задаются все элементы множества.
Множество всех континентов Земли:
Множество букв слова «математика»:
Множество натуральных чисел меньших 5:
2) Характеристическое свойство – указывается особенность элементов множества.
D =
3) Графическое изображение – визуальное моделирование с помощью различных диаграмм (круги Эйлера, интервалы, графики и т.п.)
Подмножества
Говорят, что B содержит A, или B покрывает A.
Пустое множество является подмножеством любого множества.
Множество людей является подмножеством приматов, живущих на Земле.
Множество квадратов является подмножеством прямоугольников.
Множество всех подмножеств данного множества A называют булеаном или степенью множества A.
Примеры
Пример 1. Запишите данное множество с помощью перечисления элементов:
Задано множество целых чисел, квадрат которых меньше 5. Перечисляем:
Задано множество целых чисел, модуль которых не больше 3. Перечисляем:
Задано множество рациональных чисел, являющихся корнями уравнения
(x-1)(2x+5) = 0. Перечисляем:
Пример 2. Запишите данное множество с помощью характеристического свойства:
а) Множество всех натуральных чисел меньше 10
б) Множество всех действительных чисел, кроме 0
в) Множество всех точек с целыми координатами, принадлежащих прямой y = 2x+1
Пример 3. Изобразите на графике в координатной плоскости данное множество:
Задано конечное множество точек, которое можно представить перечислением:
Пример 4. Укажите и запишите с помощью перечисления одно из непустых конечных подмножеств для данного множества:
Множества,их элементы,поджмножества
Вы будете перенаправлены на Автор24
В математике совокупности объектов, объединяющие ряд объектов называют множество. Данное понятие является первичным, значит, к более простым понятиям оно не сводится.
Термин множество употребляется тогда, когда речь идет о нечисловых множествах. Например, говорят о множестве диагоналей многоугольника, о множестве точек на координатной прямой, о множестве прямых, проходящих через точку.
Виды множеств
Множества могут быть конечными и бесконечными, пустыми.
Конечным называют множество, состоящее из конечного числа элементов, но при этом конечное множество может иметь любое количество элементов.
Среди конечных множеств выделяют множество, не имеющее ни одного элемента. Такое множество называется пустым множеством.
Множество, не являющееся конечным, называют бесконечным множеством.
Подмножества
Если некоторое множество не является пустым, то из него можно выделить другие множества, которые будут являться его частями.
Например, из множества натуральных чисел можно выделить множество четных.
Обозначение множеств, подмножеств и их элементов
Готовые работы на аналогичную тему
\[38\notin А, 74\notin А,934\notin А ; 12\in A,\ <\rm :\ >54\in A.\]
Способы задания множеств
Существует два глобально различных способа задания множеств.
Первый заключается в том, что множество задается указанием всех его элементов. В таком случае говорят, что множество задано перечислением всех своих элементов или списком своих элементов. Перечислением элементов можно задать только конечные множества и при небольшом количестве элементов, входящих в него
При таком способе задания множеств говорят, что множество задано перечислением его элементов.
Равенство множеств
Множества равны в том случае, если равны их элементы. При этом если множества состоят из одних и тех же элементов, но записанных в разном порядке то эти множества различны, хотя и равны.
Например, рассмотрим множества
Эти множества будут, состоят из равных элементов, значит, они будут равны, но при этом элементы расположены в разном порядке, т.е. множества различны
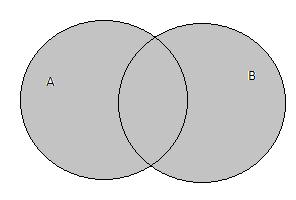
Пересечение множеств
Если даны два множества, то можно образовать новое множество, составленное из общих элементов этих множеств.
Например, рассмотрим два множества:
Объединение множеств
Математически это можно обозначить так:$\ А\ \cup B$
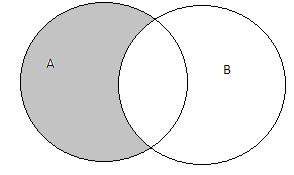
Разность множеств
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 27 05 2021
Как найти все подмножества множеств
На простом примере напомним, что называется подмножеством, какие бывают подмножества (собственные и несобственные), формулу нахождения числа всех подмножеств, а также калькулятор, который выдает множество всех подмножеств.
Пример 1. Дано множество А = <а, с, р, о>. Выпишите все подмножества
данного множества.
Решение:
Несобственные: <а, с, р, о>, Ø.
Всего: 16 подмножеств.
Пояснение. Множество A является подмножеством множества B если каждый элемент множества A содержится также в B.
• пустое множество ∅ является подмножеством любого множества, называется несобственным;
• любое множество является подмножеством самого себя, также называется несобственным;
• У любого n-элементного множества ровно 2 n подмножеств.
Последнее утверждение является формулой для нахождения числа всех подмножеств без перечисления каждого.
Для математиков сформулируем теорему и приведем строгое доказательство.
1. Для n = 1 (база индукции) (и даже для n = 2, 3) теорема доказана.
Следовательно, всех подмножеств множества B: 2 k + 2 k = 2 ⋅ 2 k = 2 k+1 штук.
Теорема доказана.
В примере 1 множество А = состоит из четырех элементов, n=4, следовательно, число всех подмножеств равно 2 4 =16.
Если вам необходимо выписать все подмножества, или составить программу для написания множества всех подмножеств, то имеется алгоритма для решения: представлять возможные комбинации в виде двоичных чисел. Поясним на примере.
Калькулятор множества всех подмножеств.
Подмножество. Основные числовые множества



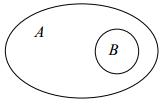
Опр. 2.1 Множество В, состоящее из некоторых элементов данного множества А (и только из них), называется подмножеством (частью) этого множества. Иначе, если любой элемент множества В принадлежит также множеству А, то множество В называется подмножеством множества А.
Это записывается так: ВÌ А или АÉВ. Говорят, что «В – подмножество А» или «В содержится в А» или «А содержит В». Заметим, что n (В) £ n (А).
Если все элементы множества А являются также элементами множества В, то говорят, что множество А включается (содержится) в множестве В.
А Ì В
Если в множестве В найдется хотя бы один элемент, не принадлежащий множеству А, то В не является подмножеством множества А: ВËА. Например, отрезок [а, b] не является подмножеством полуинтервала (а, b], т.к. аÎ[а, b], но аÏ(а, b].
Из опр. 2.1 следует, что любое множество является подмножеством самого себя, т.е. справедливо утверждение АÌА. Полагают также, что пустое множество является подмножеством любого множества. Пустое множество не содержит ни одного элемента, а значит в нем нет элемента, не принадлежащего любому другому множеству.
Знак Ì называется знаком включения. Отметим основные свойства отношения включения между множествами:
1) ÆÌА для любого множества А;
2) АÌА для любого множества А (рефлексивность);
3) из того, что ВÌА не следует АÌВ (не симметричность);
4) если АÌВ и ВÌА, то А=В (антисимметричность);
5) если АÌВ и ВÌС, то АÌС (транзитивность).
Основные числовые множества:
N= <1,2,3,4,…>– множество натуральных чисел;
Z= <…,-4,-3,-2,-1,0,1,2,3,4,…>– множество целых чисел (содержит все натуральные числа и числа, им противоположные), NÌZ;
Q=
R=(-∞;+∞) – множество действительных чисел, QÌR (кроме всех рациональных чисел, содержит иррациональные числа, содержащие в своей записи знаки радикалов: 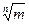
Действительные числа изображаются точками координатной прямой (числовой оси). Координатная прямая – это всякая прямая (обычно горизонтальная), на которой указаны положительное направление, начало отсчета и единичный отрезок.
Таблица 1. Правила изображения числовых промежутков.













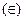 и вхождения одного множества в другое
и вхождения одного множества в другое 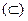 . Можно привести следующий пример. Пусть А – множество всех студентов данной группы, а В – множество всех учебных групп данного института. Здесь
. Можно привести следующий пример. Пусть А – множество всех студентов данной группы, а В – множество всех учебных групп данного института. Здесь 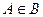 , но
, но 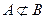 , поскольку элементы этих множеств разнородны. Этот пример показывает также, что элементами множеств могут являться другие множества.
, поскольку элементы этих множеств разнородны. Этот пример показывает также, что элементами множеств могут являться другие множества.
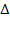 B:
B: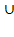 ( B\A ).
( B\A ).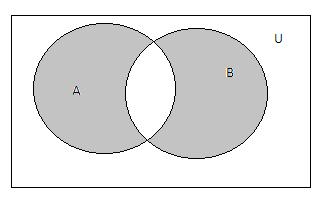
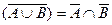
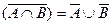 (3).
(3).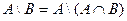
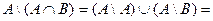 Æ
Æ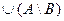 = A \ В
= A \ В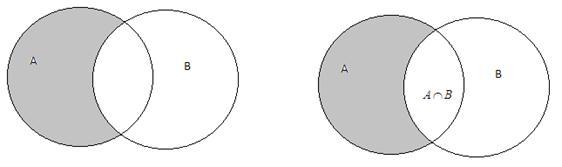
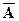 –множество не отличников;
–множество не отличников;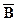 –множество не спортсменов.
–множество не спортсменов.