Что называется периметром многоугольника 8 класс

Многоугольники

Многоугольник — это геометрическая фигура, ограниченная замкнутой ломаной линией, не имеющей самопересечений.

Звенья ломаной называются сторонами многоугольника, а её вершины — вершинами многоугольника.

Углами многоугольника называются внутренние углы, образованные соседними сторонами. Число углов многоугольника равно числу его вершин и сторон.

Многоугольникам даются названия по количеству сторон. Многоугольник с наименьшим количеством сторон называется треугольником, он имеет всего три стороны. Многоугольник с четырьмя сторонами называется четырёхугольником, с пятью — пятиугольником и т. д.

Обозначение многоугольника составляют из букв, стоящих при его вершинах, называя их по порядку (по часовой или против часовой стрелки). Например, говорят или пишут: пятиугольник ABCDE :

В пятиугольнике ABCDE точки A, B, C, D и E — это вершины пятиугольника, а отрезки AB, BC, CD, DE и EA — стороны пятиугольника.

Выпуклые и вогнутые

Многоугольник называется выпуклым, если ни одна из его сторон, продолженная до прямой линии, его не пересекает. В обратном случае многоугольник называется вогнутым:

Периметр

Сумма длин всех сторон многоугольника называется его периметром.

Периметр многоугольника ABCDE равен:

Если у многоугольника равны все стороны и все углы, то его называют правильным. Правильными многоугольниками могут быть только выпуклые многоугольники.

Диагональ

Диагональ многоугольника — это отрезок, соединяющий вершины двух углов, не имеющих общей стороны. Например, отрезок AD является диагональю:

Единственным многоугольником, который не имеет ни одной диагонали, является треугольник, так как в нём нет углов, не имеющих общих сторон.

Если из какой-нибудь вершины многоугольника провести все возможные диагонали, то они разделят многоугольник на треугольники:

Треугольников будет ровно на два меньше, чем сторон:

где t — это количество треугольников, а n — количество сторон.

Разделение многоугольника на треугольники с помощью диагоналей используется для нахождения площади многоугольника, так как чтобы найти площадь какого-нибудь многоугольника, нужно разбить его на треугольники, найти площадь этих треугольников и полученные результаты сложить.

Источник

Периметр многоугольника

Чтобы найти длину ломаной линии, нужно сложить длины ее отрезков-звеньев.

В математике периметр обозначают буквой P (пэ).

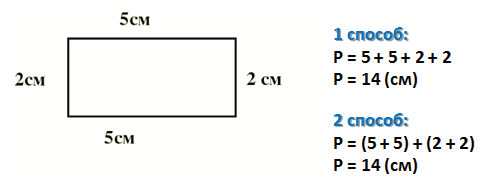
Периметр прямоугольника

Например, найдём периметр данного прямоугольника.

Этим способом мы пользуемся до тех пор, пока не выучили действие умножение.

Мы знаем, что периметр прямоугольника – сумма длин всех его сторон.

Формула для подсчета периметра прямоугольника:

(a + b) • 2

a – длина прямоугольника

b – ширина прямоугольника.

Сумма длины и ширины (a + b) называется полупериметром, чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.

Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 2 см и 6 см:

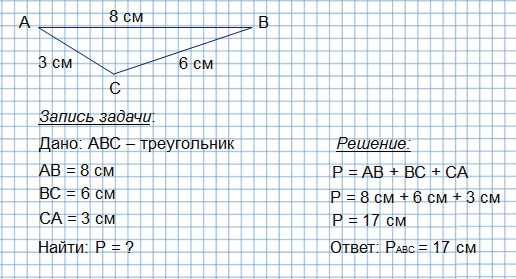
Периметр треугольника

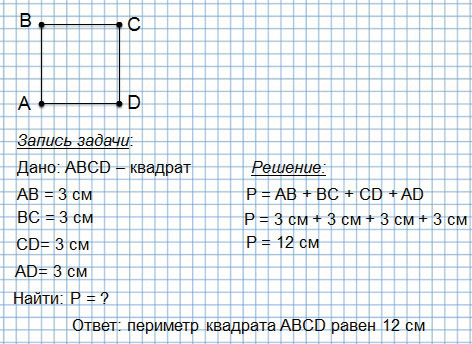
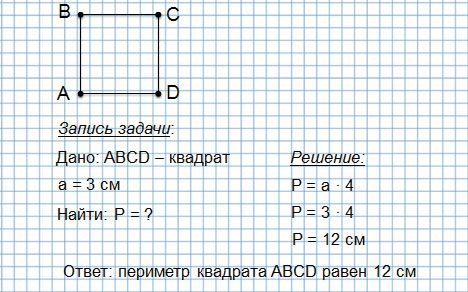
Периметр квадрата

Первый способ (когда мы еще не знаем действие умножения):

Второй способ (когда мы изучили действие умножения):

Поделись с друзьями в социальных сетях:

Источник

Как найти периметр фигуры

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Определение периметра

Периметр — это сумма длин всех сторон многоугольника.

Какой буквой обозначается периметр? Заглавной латинской P. Под обозначением P удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

В чем измеряется периметр? В тех же единицах измерения, что и длина — например, миллиметр, сантиметр, метр, фут, дюйм, локоть и др.

Если в условиях задачки длины сторон переданы в разных единицах длины, мы не сможем узнать периметр фигуры. Для правильного решения нужно перевести все данные в одну единицу измерения.

Формулы нахождения периметра

Как мы только что узнали, периметр — это сумма длин всех сторон многоугольника. А значит, чтобы его найти, нам надо знать длины этих сторон. Давайте посмотрим, как найти периметр, на примерах нескольких фигур.

Равносторонний многоугольник

У равностороннего треугольника все стороны равны. А значит, периметр равностороннего треугольника можно найти как произведение длины стороны на их количество, т. е. на 3.

P = 3 ⋅ a, где a — длина стороны.

Периметр любого другого равностороннего многоугольника можно найти тем же способом: умножив длину его стороны на их количество. Например, у квадрата и ромба все стороны равны, а значит, их периметр можно найти по формуле P = 4 ⋅ a, где a — длина стороны.

А формула для любого равностороннего n-угольника будет такая: P = n ⋅ a, где a — длина стороны, n — количество сторон.

Прямоугольник и параллелограмм

У прямоугольника и параллелограмма противоположные стороны равны, а значит, найти их периметр легко, зная две соседние стороны.

P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.

Окружность

У окружности нет периметра, потому что это не многоугольник. Но у нее есть длина, которую можно найти, зная радиус. Длина окружности — это произведение пи на два радиуса или произведение пи на диаметр.

L = d ⋅ π = 2 ⋅ r ⋅ π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.

Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!

Решение задач

Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?

Ответ: две другие стороны равны по 17 см.

Радиус окружности равен периметру равностороннего пятиугольника со стороной 4 см. Найдите длину окружности.

Еще больше практических заданий — на курсах по математике в онлайн-школе Skysmart!

Источник

Конспект урока математики «Многоугольники. Периметр»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Тема урока: Многоугольники. Периметр многоугольника.

Цели: познакомить обучающихся с понятием «многоугольник» и «сторона многоугольника»; знакомить учащихся с новым математическим понятием «периметр

многоугольника»; способствовать осознанию учащимися возможности находить периметр

многоугольника различными способами; способствовать самостоятельному добыванию знаний и применению их в практической деятельности.

развивать логическое мышление и пространственные представления; способствовать развитию умения делать выводы на основе собственных наблюдений, сравнения, обобщения, использования личного опыта; развивать умение рассуждать

I. Организационный момент.
Настрой на урок:

II. Устный счет. Мотивация учебной деятельности учащихся.

​​​​​​​ 1. Арифметический диктант.

Запиши число, которое на 6 меньше, чем 8

Увеличь полученное число на 6

Найди разность чисел 22 и 8

Найди сумму чисел 13 и 7

Запиши число, которое на 11 больше, чем 15

Запиши число, где 3 десятка и 2 единицы

2. Поиск закономерности в числовом ряду.

Ученики проводят взаимопроверку полученного ряда, затем объявляю:

должен получиться ряд: 2, 8, 14, 20, 26, 32

— найдите закономерность в записи этого ряда.

3. Геометрическое задание:

— Как называются эти фигуры?

а) незамкнутая ломаная

— Из чего состоит ломаная а)? (из отрезков прямой линии)

— Как называются отрезки ломаной линии? (звенья)

— Как измерить длину ломаной а)? (надо измерить длину каждого звена, полученные величины сложить)

— Как превратить ломаную а) в четырехугольник? (надо соединить концы ломаной отрезком прямой линии)

— Какая фигура здесь лишняя? Почему?
— Уберем лишнюю фигуру. Что объединяет оставшиеся фигуры? Как они называются? (Четырехугольники.)
— Послушайте внимательно задание:
нарисуйте в тетради один из этих четырехугольников, измерьте линейкой стороны вашего четырехугольника (в мм), запишите полученную величину.

Эта величина называется периметр. Дайте свое определение периметра.

Сегодня на уроке мы уточним, что же такое многоугольник, узнаем, что называют периметром и как найти периметр многоугольника.
— Многоугольники можно построить с любым количеством углов.

— Как вы думаете, наше определение периметра можно использовать для любого многоугольника? (Да)

IV. Этап усвоения новых знаний.
1. Работа с учебником
— Прочитайте задание. Сколько углов у каждой фигуры? Вспомните, как можно отметить углы, пользуясь различными обозначениями? (дуга, цифра, буква).
— Можно ли все эти фигуры назвать одним словом? (многоугольники)
— Из чего состоят всё данные фигуры? (из сторон, углов, вершин)
— А от чего будет зависеть название каждой отдельной фигуры?
Продолжить читать задание в учебнике.
— Верно ли утверждение, что количество углов в каждом многоугольнике равно количеству его сторон?

2. Коллективная работа
Чем похожи: количеством углов, вершин, сторон. Как одним словом можно назвать эти многоугольники? (пятиугольники)?
В чем отличия: форма, цвет.
— Что нужно сделать, чтобы найти сумму длин всех сторон многоугольника? Измеряем стороны фигуры № 2 (правильный пятиугольник) в мм.
— Что заметили интересного? (все стороны одинаковы по длине)
Результаты записываем в тетрадь, озвучиваем решение и ответ.

3. Объяснение понятия «периметр».

— Понятие «периметр» появилось в древние времена, когда было нужно измерить

границы земельных участков. Слово «периметр» образовано сложением греческих слов «пери» — «кругом, вокруг» и «метрон» — «мера». Землемеры ходили вокруг участка и мерили границы шагами.

— Как вы думаете, а кому сейчас нужно знание периметра? (Строителям, архитекторам, швеям, землемерам, …)

— Ваши родители пришли покупать плинтус для потолка в комнате. Что им надо измерить до прихода в магазин?

— Математики решили обозначать периметр латинской буквой Р.

VI. Первичное закрепление знаний и проверка понимания изученного.

1. Практическая работа с линейкой и циркулем
— Что нужно сделать для выполнения задания? (измерить в мм стороны первого треугольника при помощи линейки).
— Найдем периметр треугольника. (У доски один ученик)
— Каким свойством сложения можно пользоваться при вычислении периметра? (сочетательным)

— Посмотрите на слайд. Каждая буква имени занимает одну клетку.

Запишите в тетради имя соседа по парте таким же образом, обведите имя так, как показано на слайде.

— Какая фигура получилась? Сосчитайте периметр этой фигуры, сравните с результатом соседа.

3. Самостоятельная работа.

Раздаются карточки с четырехугольниками (по вариантам). Задание: вычислить периметр этого четырехугольника в сантиметрах (на обратной стороне – правильный ответ, записанный в виде суммы сторон фигуры, например,

2+4+2+4 = 12 см). После выполнения работы предлагается посмотреть ответ и провести анализ возможных ошибок.

Инструктаж. Выставление отметок за активную работу на уроке.

Продолжим фразу…
— Что нового узнали на уроке?
— Что такое периметр многоугольника?
— Как найти периметр многоугольника?
— Где применяется знание о периметре в жизни?
— Спасибо всем за урок.

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Источник

Многоугольник

Определение 1. Многоугольник − замкнутая ломаная линия.

Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:

Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.

Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.

Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.

Виды многоугольников

Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с \( \small n \) вершинами называется \( \small n- \)угольником.

На рисунке 1 представлены различные виды многоугольников.

Обозначение многоугольника

Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют \( \small A_1A_2A_3A_4A_5A_6 \) или \( \small A_6A_5A_4A_3A_2A_1 \).

Соседние вершины многоугольника

Вершины многоугольника называются соседними, если они являются концами одной из его сторон.

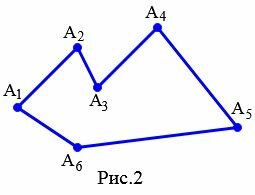На рисунке 2 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)

Смежные стороны многоугольника

Стороны многоугольника называются смежными, если они имеют общую вершину.

На рисунке 2 стороны \( \small A_4A_5 \) и \( \small A_5A_6 \) являются смежными, так как они имеют общую вершину \( \small A_5. \)

Простой многоугольник. Самопересекающийся многоугольник

Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).

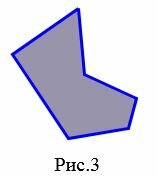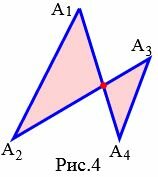На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой многоугольник называется самопересекающийся многоугольник.

Выпуклый многоугольник

Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.

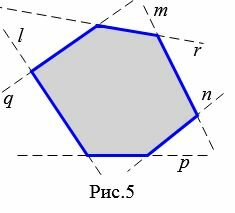На рисунке 5 многоугольник лежит по одну сторону от прямых \( \small m, \ n, \ l, \ p, \ q, \ r\) проходящих через стороны многоугольника.

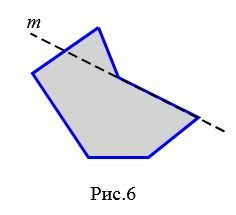На рисунке 6 прямая \( \small m\) делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой \( \small m\). Следовательно многоугольник не является выпуклым.

Правильный многоугольник

Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.

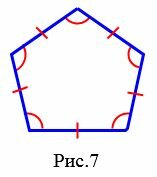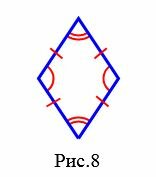На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.

Звездчатый многоугольник

Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.

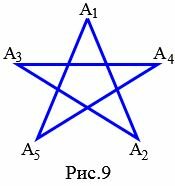На рисунке 9 представлен звездчатый пятиугольник поскольку все углы \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) равны и равны все стороны: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)

Периметр многоугольника

Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника \( \small A_1A_2. A_A_n \) периметр вычисляется из формулы:

Угол многоугольника

Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small A_3 \) на рисунке 2).

Внешний угол многоугольника

Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.

На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине \( \small E. \)

Диагональ многоугольника. Количество диагоналей

Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.

Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:

Сумма углов выпуклого многоугольника

Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины \( \small A_1 \) все диагноали многоугольника \( \small A_1A_2. A_A_n \) (Рис.11):

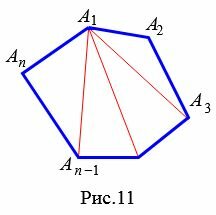Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно \( \small n-3 \). Следовательно, эти диагонали разделяют многоугольник на \( \small n-3+1=n-2 \) треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: \( \small 180°(n-2). \)

где \( \small n \) −количество сторон (вершин) выпуклого многоугольника.

Угол правильного многоугольника

Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:

где \( \small n \) −количество сторон (вершин) правильного многоугольника.

Источник