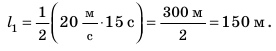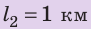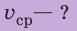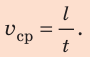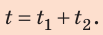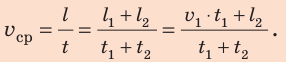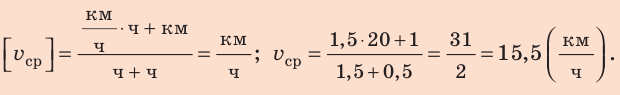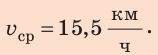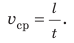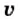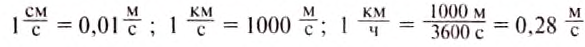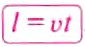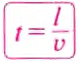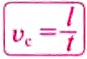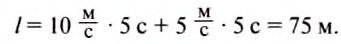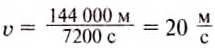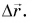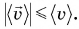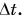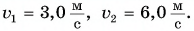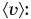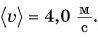Что называется неравномерным движением в физике
Неравномерное движение
Вы будете перенаправлены на Автор24
В реальной жизни очень сложно встретить равномерное движения, так как с такой большой точностью объекты материального мира не могут передвигаться, да еще и долгий промежуток времени, поэтому обычно на практике используются более реальное физическое понятие, характеризующее движение определенного тела в пространстве и времени.
Неравномерное движение характеризуется тем, что тело может проходить одинаковый или разный путь за равные промежутки времени.
Для полного понимания этого вида механического движения вводится дополнительное понятие средней скорости.
Средняя скорость
Средняя скорость представляет собой физическую величину, которая равна отношению всего пути, пройденного телом, к полному времени движения.
Этот показатель рассматривается на определенном участке:
По данному определению средняя скорость является скалярной величиной, так как время и путь – скалярные величины.
Средняя скорость можно определять по уравнению перемещения:
Средняя скорость в подобных случаях считается векторной величиной, так как она ее можно определить через отношение векторной величины к скалярной.
Средняя скорость перемещения и средняя скорость прохождения пути характеризуют одинаковое движение, однако являются различными величинами.
В процессе расчета средней скорости обычно допускается ошибка. Она состоит в том, что понятие средней скорости иногда заменяется средней арифметической скоростью тела. Этот недочет допускается на разных участках движения тела.
Средняя скорость тела не может определяться через среднее арифметическое значение. Для решения задач используется уравнение для средней скорости. По нему можно найти среднюю скорость тела на определенном участке. Для этого весь путь, который пройден телом, разделить на общее время движения.
Готовые работы на аналогичную тему
Получается формула, согласно которой идет поиск неизвестной величины:
При решении длинной цепочки уравнений можно прийти к изначальной версии поиска средней скорости тела на определенном участке.
При непрерывном движении также непрерывно изменяется скорость тела. Подобное движение рождает закономерность, при которой скорость в любой последующих точках траектории отличается от скорости объекта в предыдущей точке.
Мгновенная скорость
Мгновенной скоростью называют скорость в данный отрезок времени в определенной точке траектории.
Средняя скорость тела будет сильнее отличаться от мгновенной скорости в случаях, когда:
Мгновенная скорость – это физическая величина, которая равна отношению небольшого перемещения на определенном участке траектории или пройденного пути телом, к небольшому промежутку времени, за которое это перемещение совершалось.
Мгновенная скорость становится векторной величиной, когда речь идет о средней скорости перемещения.
Мгновенная скорость становится скалярной величиной, когда говорят о средней скорости прохождения пути.
При неравномерном движении изменение скорости тела происходит за равные промежутки времени на равную величину.
Равнопеременное движение тела возникает в момент, когда скорость объекта за любые равные промежутки времени изменяется на равную величину.
Виды неравномерного движения
При неравномерном движении постоянно меняется скорость тела. Различают основные виды неравномерного движения:
Скорость может изменяться по численному значению. Подобное движение также считают неравномерным. Особенным случаем неравномерного движения считают равноускоренное движение.
Неравнопеременным движением называют такое движение тела, когда скорость объекта за любые неравные промежутки времени не меняется на определенную величину.
Равнопеременное движение характеризуется возможностью увеличения или уменьшения скорости тела.
Равнозамедленным называют движение, когда скорость тела уменьшается. Равноускоренным называют движение, при котором скорость тела увеличивается.
Ускорение
Для неравномерного движения введена еще одна характеристика. Эта физическая величина называется ускорением.
Ускорением называют векторную физическую величину, равная отношению изменения скорости тела ко времени, когда это изменение происходило.
При равнопеременном движении нет зависимости ускорения от изменения скорости тела, а также от времени изменения этой скорости.
Ускорение показывает на количественное изменение скорости тела за определенную единицу времени.
Для того, чтобы получить единицу ускорения, необходимо в классическую формулу для ускорения подставить единицы скорости и времени.
В проекции на координатную ось 0X уравнение примет следующий вид:
$υx = υ0x + ax ∙ \Delta t$.
Если знать ускорение тела и его начальную скорость, можно заранее найти скорость в любой заданный момент времени.
Физическая величина, которая равна отношению пути, пройденного телом за конкретный промежуток времени, к длительности подобного промежутка, является средней путевой скоростью. Средняя путевая скорость выражается в виде:
Средняя скорость представлена в форме вектора. Она направлена туда, куда направлено перемещение тела за определенный промежуток времени.
Модуль средней скорости равняется средней путевой скорости в случаях, если тело все это время движется в одном направлении. Модуль средней скорости уменьшается к средней путевой скорости, если в процессе движения тело изменяет направление своего движения.
Содержание:
Неравномерное движение:
Наверняка вам случалось ехать на автобусе или автомобиле из одного города в другой. Вспомните: транспортное средство время от времени тормозит, останавливается, потом снова набирает скорость… Стрелка спидометра все время колеблется и только иногда замирает на месте. Можно ли назвать такое движение равномерным? Конечно, нет. А как называют такое движение? Как его описывают?
В повседневной жизни мы обычно имеем дело с неравномерным движением. Так, неравномерным является движение автобуса (рис. 11.1) и других транспортных средств, движение падающих тел, движение спортсменов на беговой дорожке. А еще вспомните, например, как катится мяч, как вы движетесь во время прогулки, на уроках физкультуры и т. д.
Вычисляем среднюю скорость движения тела
Предположим, что поезд прошел 150 км (расстояние между двумя станциями) за 2,5 ч. Если разделить 150 км на 2,5 ч, получим скорость движения поезда — 60 км/ч. Но ведь поезд двигался неравномерно! В таком случае говорят, что получена средняя скорость движения поезда (рис. 11.2).
Средняя скорость движения тела 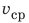
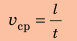
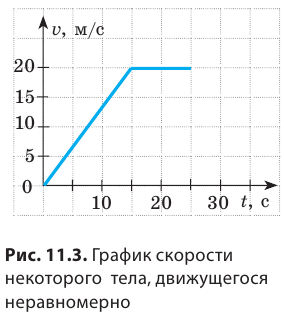
График скорости неравномерного движения тела
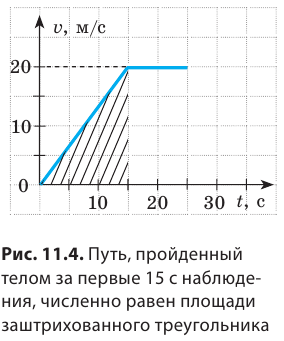
Рассмотрим график скорости неравномерного движения некоторого тела (рис. 11.3) и определим: как двигалось тело; какой путь прошло тело за 25 с наблюдения; какой была средняя скорость движения тела на данном пути. По графику видим, что скорость движения тела в течение первых 15 с равномерно увеличивалась от 0 до 20 м/с. Чтобы вычислить путь, пройденный телом за это время, вспомним: числовое значение пути, который прошло тело, равно числовому значению площади фигуры под графиком скорости движения этого тела. Итак, определим площадь заштрихованного треугольника (рис. 11.4). Из рисунка видим, что площадь заштрихованного треугольника равна половине площади прямоугольника с «длиной» 20 м/с и «шириной» 15 с. Площадь прямоугольника, в свою очередь, равна произведению его длины и ширины. Таким образом, путь 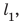
Следующий интервал времени 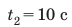
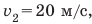
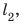
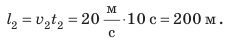
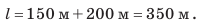
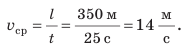
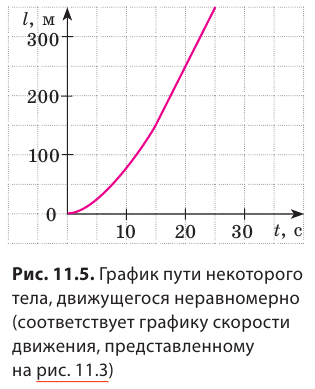
Обратите внимание! Путь не может уменьшаться, поэтому график пути либо поднимается, либо остается горизонтальным, но никогда не опускается.
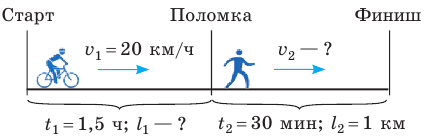
Пример
Полтора часа мальчик ехал на велосипеде со скоростью 20 км/ч. Потом велосипед сломался, и последний километр пути мальчик шел пешком. Какой была средняя скорость движения мальчика на всем пути, если пешком он шел полчаса? Анализ физической проблемы. Выполним пояснительный рисунок. Для определения средней скорости движения нужно найти путь, который преодолел мальчик, и время его движения. Время движения выражено в часах, путь — в километрах, поэтому среднюю скорость движения найдем в километрах в час.
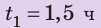
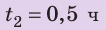
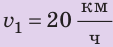
Решение:
По определению:
Путь l, который преодолел мальчик, равен: 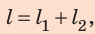
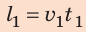
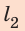
Подставив выражения для l и t в формулу средней скорости движения, получим:
Проверим единицу, найдем значение искомой величины:
Анализ результатов. Мальчик ехал на велосипеде со скоростью 20 км/ч, шел пешком со скоростью 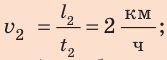
Ответ:
Итоги:
Неравномерное движение — это движение, при котором тело за равные интервалы времени проходит разный путь. Виды механического движения: по форме траектории — прямолинейное и криволинейное; по зависимости скорости движения от времени — равномерное и неравномерное. Средняя скорость движения тела равна отношению всего пути, пройденного телом, к интервалу времени, за который этот путь пройден:
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Содержание:
Равномерное движение:
Если тело за первую секунду прошло путь 5 м, за вторую — снова 5 м, за третью — 5 м и т. д., т. е. за каждую любую секунду тело проходит одинаковый путь, то такое движение является равномерным.
Опыт. Возьмём стеклянную трубку длиной 1 м и диаметром 1 см (рис. 4). Закроем её с обеих сторон пробками, предварительно налив в неё воды так, чтобы в ней остался воздушный пузырёк. Теперь установим трубку вертикально или с наклоном так, чтобы в начальный момент воздушный пузырёк был расположен в нижнем конце трубки. Пузырёк начнёт медленно всплывать, и будет удобно наблюдать за характером его движения. В результате опыта убеждаемся, что пузырёк воздуха будет проходить одинаковые отрезки пути за одинаковые интервалы времени. Итак, движение пузырька является равномерным.
Равномерным движением называют такое движение, при котором тело за любые одинаковые интервалы времени проходит одинаковый путь.
Примером равномерного движения является движение точки земной поверхности при обращении Земли вокруг своей оси. Равномерным можно считать движение точек часовых стрелок, равномерно может двигаться автомобиль по прямой и ровной дороге.
При неравномерном движении тело за одинаковые интервалы времени проходит неодинаковый путь.
Скорость движения и единицы скорости
Лодку, равномерно движущуюся по поверхности моря, обгоняют дельфины, плывущие также равномерно. Чем различаются эти равномерные движения: лодки и дельфинов? Их отличие состоит в том, что дельфины движутся быстрее лодки. Самолёт движется быстрее поезда, но медленнее, чем искусственный спутник Земли. А это означает, что на протяжении одинакового интервала времени дельфины проплывают больший путь, чем лодка, самолёт пролетает больший путь, чем проходит поезд, а спутник — больший путь, чем самолёт.
Движения лодки, дельфинов, поезда, самолета и спутника различаются их скоростью. Говорят, что то тело, которое за единицу времени проходит больший путь, движется с большей скоростью.
Например, если за каждый час автомобиль проезжает 60 км, а самолет пролетает 600 км, то говорят, что скорость движения автомобиля равняется 60 км в час, а скорость движения самолёта — 600 км в час.
Скорость движения тела обозначают малой латинской буквой
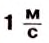
Применяют ещё такие единицы скорости движения тела:
Чтобы определить скорость равномерного движения тела, нужно путь, пройденный телом за определённый интервал времени, разделить на этот интервал: 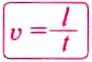
где 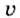
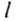
t — время движения тела.
В отличие от других физических величин значения скоростей лежат в определённых пределах: от 0 (когда тело находится в покое) до скорости распространения света в безвоздушном пространстве, которая равна 300 000 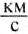
Скорость обычной ходьбы человека равна 1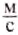
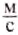
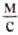
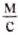
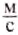
Однако человек создал транспортные средства, развивающие значительные скорости. Гепард уже не может соревноваться с легковым автомобилем, поездом или мотоциклом. Специальные гоночные автомобили развивают скорость до
284 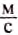
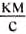
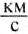
Скорость движения тела характеризуется не только числовым значением, но и направлением. Например, чтобы узнать, где будет находиться через 5 ч путешествия турист, вышедший из Киева, нужно знать не только с какой скоростью он движется, а и в каком направлении (направление скорости).
Величины, зависящие от направления в пространстве, называют векторными величинами, или векторами.
Скорость движения тела является векторной величиной.
На рисунках вектор скорости изображают стрелкой, направление которой совпадает с направлением скорости, а длина равна числовому значению скорости в определенном масштабе (рис. 5).
Зная скорость равномерного движения тела, можно определить путь, который оно проходит за определённое время. Пусть, например, велосипедист движется со скоростью 5 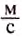
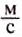
Чтобы определить путь, который тело проходит при равномерном движении, нужно скорость движения тела умножить на время его движения:
Зная путь и скорость равномерного движения тела, можем определить время его движения. Например, за какое время пловец переплывёт озеро шириною 200 м, если он движется со скоростью 2 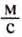
За 1 с он проплывает 2 м. Чтобы определить, сколько секунд он затратит на то, чтобы проплыть 200 м, нужно узнать, сколько раз в 200 м содержится 2 м. Для этого 200 разделим на 2 и получим 100. Время, за которое пловец переплывёт озеро, равно 100 с, или 1 мин 40 с.
Чтобы определить время движения тела, нужно пройденный телом путь разделить на скорость движения тела:
Это интересно знать:
Американская ящерица бегает по воде, как по твёрдой земле, со скоростью 11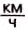
Средняя скорость неравномерного движения
Если тело движется неравномерно, то за одинаковые интервалы времени оно проходит неодинаковые пути. Из этого можем сделать вывод, что скорость движения тела за каждый интервал времени изменяется.
Значения скоростей движения в живой и неживой природе лежат в широком интервале, некоторые из них приведены в таблице 1.
Скорости движения в природе, 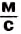
Не все указанные в табл. 1 движения являются равномерными. Лишь звук и свет при определённых условиях распространяются с постоянной скоростью. Скорости остальных тел изменяются во время движения. Поэтому для них указаны средние или максимально достижимые значения.
Во время неравномерного движения тела его скорость может значительно изменяться в разных точках траектории, но для упрощения часто пользуются средней скоростью неравномерного движения на определённом участке пути или за определённое время движения, условно полагая его равномерным.
Средняя скорость движения тела определяется отношением пройденного им пути к полному времени движения:
где 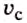
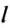
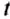
Конечно, полученные при этом значения средней скорости могут не совпадать со скоростью движения тела на отдельных участках траектории. При неравномерном движении тело на одних участках имеет меньшую скорость, на других — большую. Например, самолёт, начиная взлёт, увеличивает свою скорость, потом летит с определённой постоянной скоростью, перед посадкой уменьшает скорость движения.
Это интересно знать:
Если двигаться равномерно по прямой (скорость указана в скобках), то путешествие на Луну продолжалось бы:
Графическое изображение равномерного движения тела
Прямолинейное движение — это движение тела, траекторией которого является прямая линия. Примером прямолинейного движения может быть движение автомобиля на участке шоссе, где нет подъёмов, спусков и поворотов.
Прямолинейным равномерным движением называют такое движение, при котором тело за любые равные интервалы времени проходит одинаковые пути по прямолинейной траектории.
Прямолинейное равномерное движение тела очень удобно представлять и изучать в виде графиков зависимости пройденного телом пути от времени его движения (график движения) и зависимости скорости тела от времени его движения (график скорости).
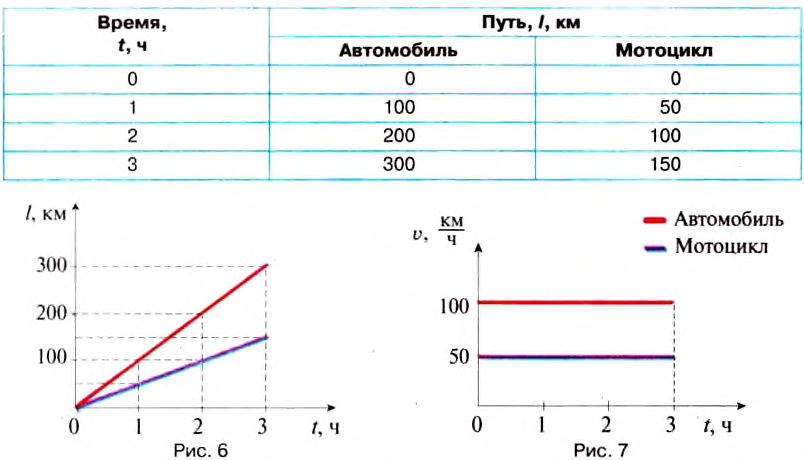
Рассмотрим пример. Пусть автомобиль движется из Киева в Одессу со скоростью 100 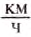
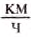
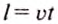
Чтобы построить график зависимости скорости движения тела от времени движения, или график скорости, нужно на вертикальной оси отложить значения скорости 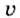
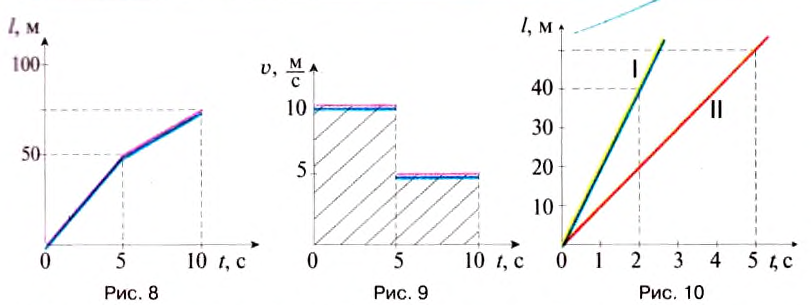
Теперь рассмотрим другой случай. Пусть велосипедист двигался 5 с
со скоростью 10 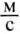
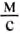
Из графика движения (рис. 8) видно, что на пятой секунде велосипедист уменьшил скорость движения, поэтому и наклон прямой уменьшился. Графиком такого движения является ломаная.
График зависимости скорости движения от времени (рис. 9) имеет вид ступенчатой линии — «ступеньки», которая образовалась также из-за уменьшения вдвое скорости движения велосипедиста на пятой секунде.
Рассмотрим заштрихованную фигуру под графиком скорости: она состоит из двух прямоугольников. Оказывается, что, определяя площадь этих прямоугольников как произведение их высоты и длины, мы умножаем скорость движения велосипедиста на время его движения и определяем пройденный им путь на обоих участках:
Из расчётов видно, что результат совпадает с данными в таблице.
Как видим, по графикам движения и скорости можно полностью определить вид, скорость, время и путь движения тела.
Пример №1
Если велосипедист за первые 5 мин проехал 5 км, а за следующие 10 мин — 10 км, то можно ли считать такое движение равномерным?
Ответ: да, так как велосипедист двигался с одинаковой скоростью — 1
Пример №2
Легковой автомобиль проходит расстояние 144 км за 2 ч. Определить скорость движения автомобиля, считая его движение равномерным.
Дано:
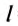
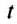
Решение:
Для расчета скорости движения автомобиля используем формулу:
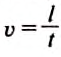
Переведём километры в метры, а часы — в секунды.
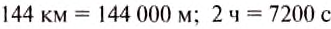
Тогда
Ответ: скорость движения автомобиля равна 72 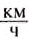
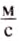
Неравномерное движение. Средняя и мгновенная скорость
Мы изучили равномерное прямолинейное движение. Однако реальные тела — люди, автомобили, корабли, самолеты и др. — чаще всего движутся и не прямолинейно, и не равномерно. Каковы закономерности таких движений?
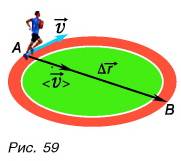
Рассмотрим пример. По дорожке стадиона бежит легкоатлет, то увеличивая, то уменьшая скорость бега (рис. 59).
Движение легкоатлета и не прямолинейное, и не равномерное. Как описать такое движение? Из 7-го класса вам известно, что неравномерное движение характеризуют средней скоростью. Ее определяют как отношение пути к промежутку времени, за который этот путь пройден:
В нашем примере путь s — это длина дуги АВ, а 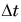
Более точно называть 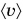
Средняя скорость пути ничего не говорит о направлении движения. Поэтому, кроме нее, вводят среднюю скорость перемещения, равную отношению перемещения 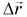
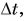
Из векторного равенства (2) следует, что средняя скорость перемещения 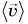
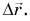
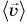
Каков смысл средней скорости перемещения 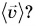
Сравнив формулу (2) с формулой 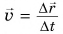
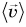
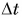
Средняя скорость пути 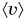
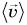
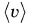
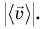
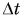
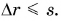
Средняя скорость характеризует движение за весь промежуток времени в целом. Она не дает информации о скорости движения в каждой точке траектории (в каждый момент времени). С этой целью вводится мгновенная скорость 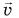
Как найти мгновенную скорость? Ее можно найти по формуле 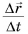
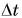
Обозначение 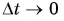
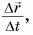
Как направлена мгновенная скорость 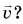
Понаблюдайте за раскаленными частицами, отрывающимися от точильного камня (рис. 60). Мгновенная скорость этих частиц в момент отрыва направлена по касательной к окружности, по которой они двигались до отрыва. Аналогично спортивный молот (рис. 61) начинает свой полет по касательной к той траектории, по которой он двигался при раскручивании метателем. Мгновенная скорость 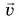
В дальнейшем мгновенную скорость будем называть просто скоростью.
Главные выводы:
Пример №3
Первую половину прямолинейной дистанции лыжник двигался с постоянной скоростью 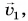
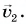

Решение
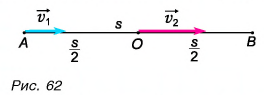
Сделаем рисунок к задаче (рис. 62):
Поскольку лыжник двигался без изменения направления, его средняя скорость направлена так же, как скорости 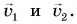
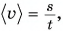
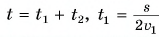
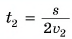

Ответ:
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.