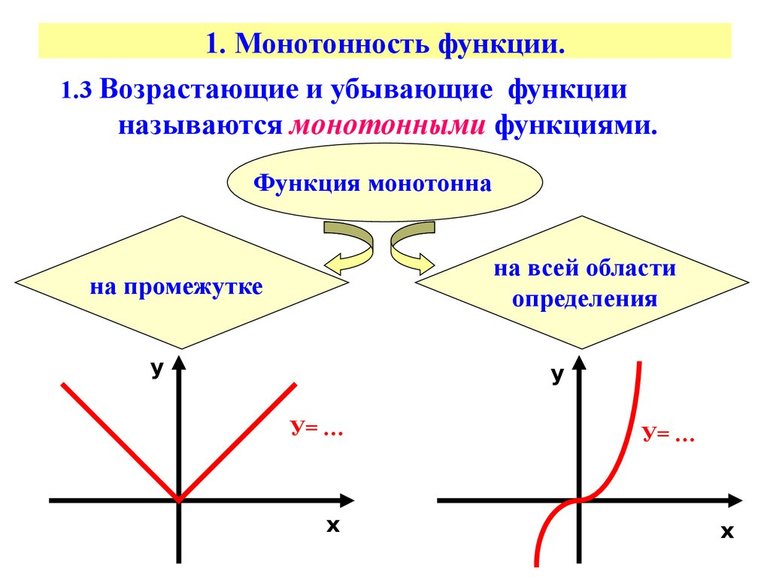
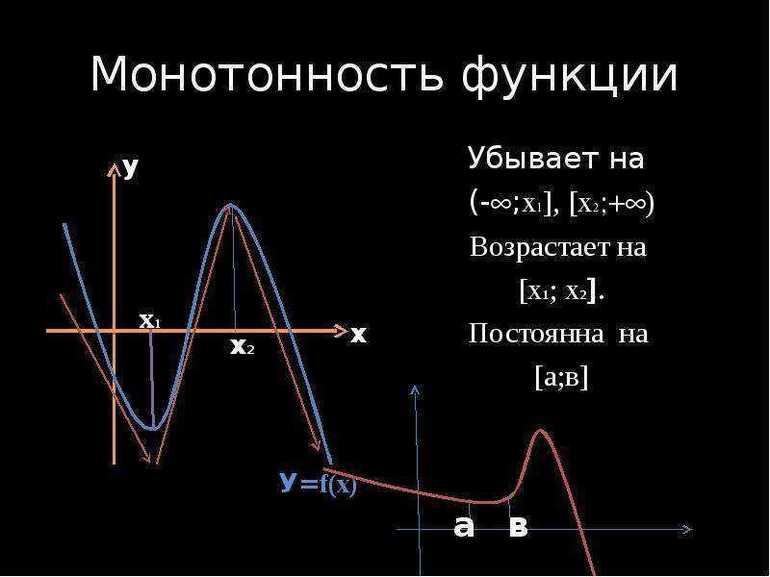
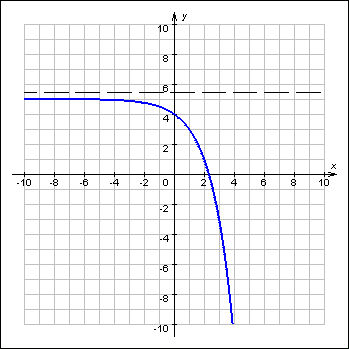
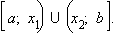Что называется монотонностью функции

Общие сведения

Функцией вида р = f(r) называется зависимость ее значения от переменной величины «r» или аргумента. Функциональные тождества бывают простыми и сложными. К первым относится класс выражений, состоящих из одной переменной простого типа. Во втором случае содержится несколько аргументов или аргумент является также функцией, т. е. подчиняется определенному закону.

Монотонной называется функция, постоянно убывающая или возрастающая на заданном промежутке. Если она постоянно убывает или возрастает, то считается строго монотонной. Пусть дана функция р = f(r). Она дифференцируема на некотором интервале (а;b), является возрастающей или убывающей, когда справедливы равенства f(r1) = f(r2) соответственно. Кроме того, нужно учитывать, что r1 =» следует заменить на строгий « »: f(r1) f(r2) соответственно. Вышеописанные понятия можно записать математическим способом, который считается более компактным:

Следует отметить, что промежутками монотонности функции называются интервалы, на которых она возрастает или убывает. После определений необходимо рассмотреть основные теоремы, позволяющие использовать соотношения для решения различных задач.

Теорема о пределе

Теорема о пределе монотонной функции применяется для решения задач по высшей математике с использованием пределов. Ее формулировка следующая: если функция вида р = f(r) является дифференцируемой и монотонной на интервале (а;b), то в точке r0, принадлежащей заданному интервалу, она имеет конечные пределы с левой и правой стороны, а в точках r0 = a и r0 = b у нее существуют правосторонние и левосторонние границы.

Чтобы понять математические обозначения sup и inf, необходимо представить множество значений функции. Первый термин обозначает максимальное значение сверху, а второй — минимальное снизу.

Критерии возрастания и убывания

Существуют определенные признаки, по которым можно определить монотонность функции p = f(r) на некотором интервале (а;b). Для этого в математике есть еще три теоремы:

Первая теорема имеет такую формулировку: дифференцируемая функция p = f(r) на интервале (а;b) является убывающей, когда выполняется неравенство f'(r) = 0 соответственно (при r ∈ данному интервалу).

Формулировка следующего утверждения только для строго возрастающей монотонной функции. В первом случае должно выполняться не одно, а два условия: f'(r) > 0 и f'(r) тождественно не эквивалентна нулю на промежутке в любой точке, принадлежащей интервалу. Для строго убывающей условия немного отличаются от предыдущих: f'(r) 0.

Основные свойства

Для функций на интервале (а;b) существуют некоторые утверждения, позволяющие исследовать составные выражения, а также решать различные задачи. К свойствам монотонных функций относятся следующие:

После изучения теорем и основных свойств нужно определить минимум базовых знаний, которые необходимы для исследования на монотонность любого выражения. Кроме того, следует знать графики некоторых функций. Для их построения можно использовать специальные онлайн-калькуляторы и программы, позволяющие выделять результаты разными цветами.

Базовые знания

Для исследования функции на монотонность специалисты рекомендуют руководствоваться некоторыми правилами, которые объединяются в универсальный алгоритм. Он является достаточным для выполнения такого задания и имеет следующий вид:

Последний пункт следует реализовывать при помощи таблицы. Необходимо строго придерживаться алгоритма, поскольку неверные действия способны существенно повлиять на результат.

Нахождение производной

Для поиска производной необходимо выполнить такие шаги: вынести константу, упростить выражение и воспользоваться таблицей дифференциалов элементарных функций (рис. 1). Первые два элемента считаются подготовительными, поскольку позволяют оптимизировать процесс вычисления. Для упрощения следует применять формулы сокращенного умножения, свойства дробей, разложение на множители и т. д. После приведения выражения к упрощенному виду нужно воспользоваться таблицей производных элементарных функций.

Рисунок 1. Дифференциалы простых выражений.

Однако при решении задач не всегда попадаются простые выражения. Для составных существуют определенные правила:

Специалисты рекомендуют для проверки использовать программы, но это не значит, что задачи должны решаться только с помощью онлайн-сервисов и математических пакетов.

Корни уравнений и критические точки

Следующим этапом является решение равенства с неизвестным. Необходимо отметить, что уравнения делятся на следующие виды: линейные, квадратные, кубические, биквадратные, тригонометрические, логарифмические, степенные, показательные и иррациональные.

Источник

Монотонность функций

Функция f (x) называется возрастающей на промежутке D, если для любых чисел x₁ и x₂ из промежутка D таких, что x₁ f (x₂).

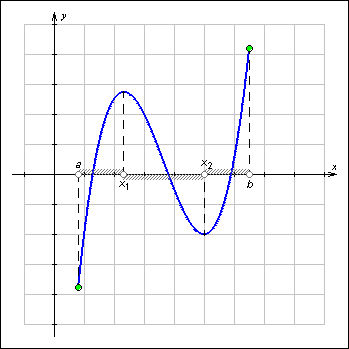Рисунок 1.3.5.1. Промежутки возрастания и убывания функции

На показанном на рисунке графике функция y = f (x), 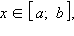возрастает на каждом из промежутков [a; x₁) и (x₂; b] и убывает на промежутке (x₁; x₂). Обратите внимание, что функция возрастает на каждом из промежутков [a; x₁) и (x₂; b], но не на объединении промежутков

Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.

Заметим, что если f – монотонная функция на промежутке D (f (x)), то уравнение f (x) = const не может иметь более одного корня на этом промежутке.

Аналогичные утверждения можно сформулировать и для убывающей функции.

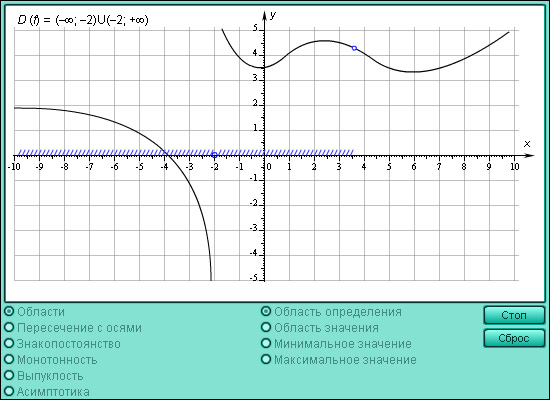Модель 1.9. Свойства функции

Точка a называется точкой максимума функции f, если существует такая ε-окрестность точки a, что для любого x из этой окрестности выполняется неравенство f (a) ≥ f (x).

Точка a называется точкой минимума функции f, если существует такая ε-окрестность точки a, что для любого x из этой окрестности выполняется неравенство f (a) ≤ f (x).

Точки, в которых достигается максимум или минимум функции, называются точками экстремума.

В точке экстремума происходит смена характера монотонности функции. Так, слева от точки экстремума функция может возрастать, а справа – убывать. Согласно определению, точка экстремума должна быть внутренней точкой области определения.

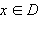
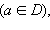
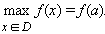Если для любого (x ≠ a) выполняется неравенство f (x) ≤ f (a) то точка a называется точкой наибольшего значения функции на множестве D:

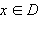
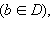
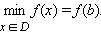Если для любого (x ≠ b) выполняется неравенство f (x) > f (b) то точка b называется точкой наименьшего значения функции на множестве D.

Точка наибольшего или наименьшего значения может быть экстремумом функции, но не обязательно им является.

Точку наибольшего (наименьшего) значения непрерывной на отрезке функции следует искать среди экстремумов этой функции и ее значений на концах отрезка.

График 1.3.5.1. Функция, ограниченная сверху

График 1.3.5.2. Функция, ограниченная снизу

График 1.3.5.3. Функция, ограниченная на множестве D.

Наибольшее и наименьшее значения функции y=f(x) на [а,b].

Источник

Монотонная функция

Определения

функция f <\displaystyle f>называется возраста́ющей на M<\displaystyle M>, если

функция f <\displaystyle f>называется стро́го возраста́ющей на M<\displaystyle M>, если

функция f <\displaystyle f>называется убыва́ющей на M<\displaystyle M>, если

функция f <\displaystyle f>называется стро́го убыва́ющей на M<\displaystyle M>, если

∀x,y∈M,x>y⇒f(x) y\Rightarrow f(x)

(Строго) возрастающая или убывающая функция называется (строго) монотонной.

Решение

Для определения промежутков возрастания и убывания функции решаем уравнение: x^<2>-2x-3=0. Решениями уравнения являются точки: x=-1 и x=3, которые разбивают числовую прямую на три отрезка. Получаем:

С отметкой о просмотре

Для доказательства достаточности критерия возрастания и убывания функции мы используем:

Элементы сортировки

Правильно
4 / 4Баллы

Неправильно
/ 4 Баллы

максимум из 8 баллов

Место	Имя	Записано	Баллы	Результат
Таблица загружается
Нет данных

Доказательство:

Литература

из 2 заданий окончено

Информация

Тест по теме Пределы монотонных функций.

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

Результаты

Правильных ответов: из 2

Вы набрали из баллов ()

Средний результат

Ваш результат

Ваш результат был записан в таблицу лидеров

С отметкой о просмотре

Количество баллов: 5

Дать определение строго монотонно возрастающей функции на отрезке

Количество баллов: 5

Вставьте пропущенные слова.
$$Если

(правосторонний) и (левосторонний) пределы.

максимум из 10 баллов

Место	Имя	Записано	Баллы	Результат
Таблица загружается
Нет данных

Условия монотонности функции

Обратное, вообще говоря, неверно. Производная строго монотонной функции может обращаться в ноль. Однако, множество точек, где производная не равна нулю, должно быть плотно на интервале (a,b). <\displaystyle (a,b).>Точнее имеет место

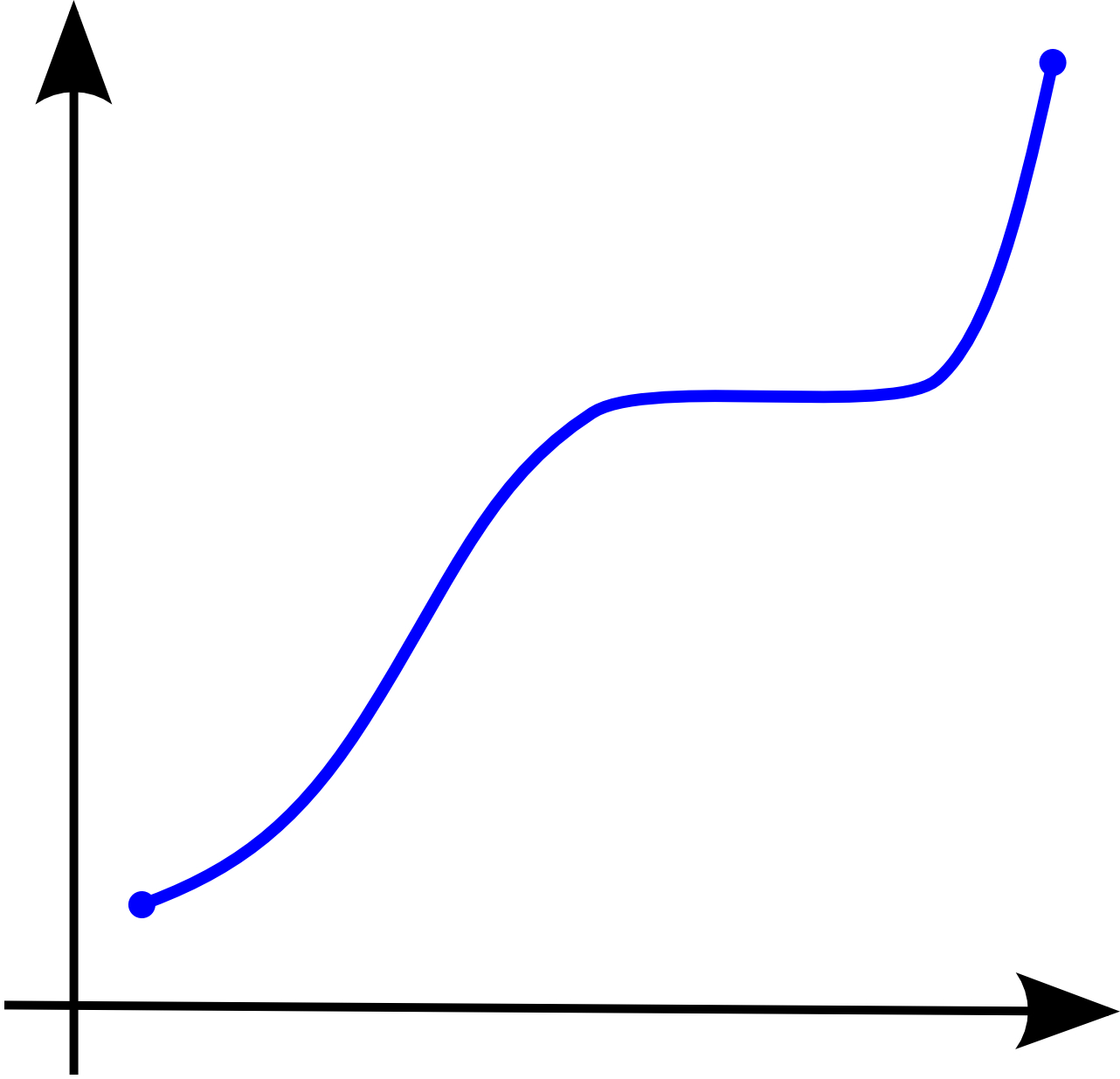
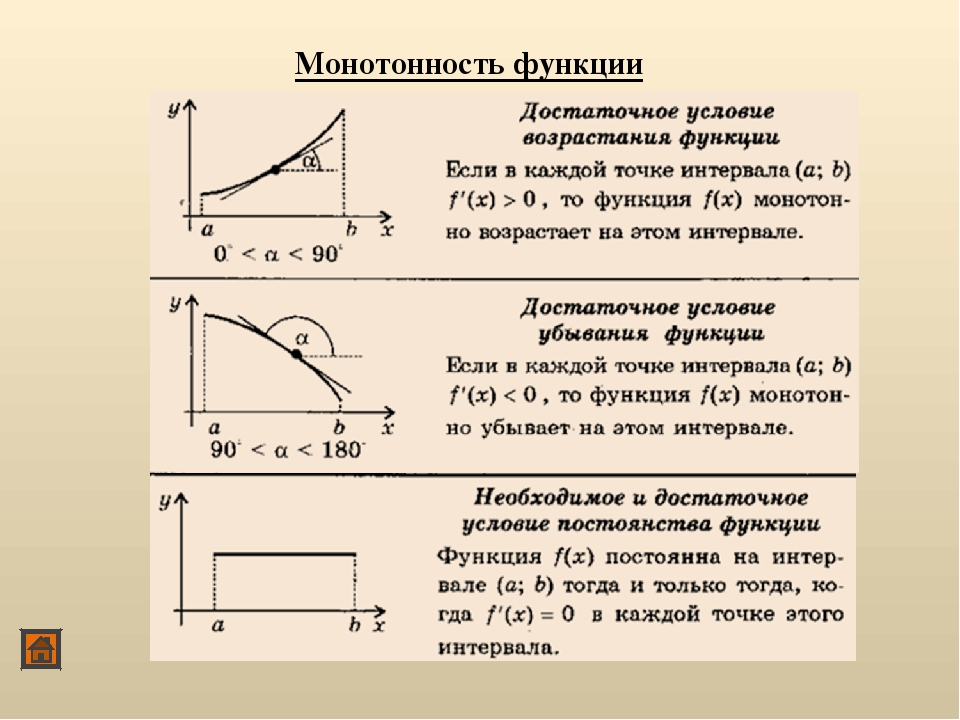
(Критерий строгой монотонности функции, имеющей производную на интервале) Пусть f∈C((a,b)),<\displaystyle f\in C<\bigl (>(a,b)<\bigr )>,> и всюду на интервале определена производная f′(x). <\displaystyle f'(x).>Тогда f <\displaystyle f>строго возрастает на интервале (a,b) <\displaystyle (a,b)>тогда и только тогда, когда выполнены следующие два условия:

Аналогично, f <\displaystyle f>строго убывает на интервале (a,b) <\displaystyle (a,b)>тогда и только тогда, когда выполнены следующие два условия:

1.3.5. Монотонность функций

Функция f (x) называется возрастающей на промежутке D, если для любых чисел x₁ и x₂ из промежутка D таких, что x₁ f (x₂).

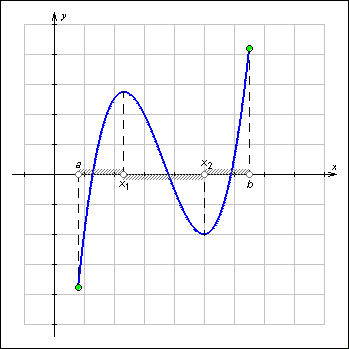Рисунок 1.3.5.1.Промежутки возрастания и убывания функции

Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.

Заметим, что если f – монотонная функция на промежутке D (f (x)), то уравнение f (x) = const не может иметь более одного корня на этом промежутке.

Действительно, если x₁ 0) и f + c также возрастают, а функция cf (c

Модель 1.9. Свойства функции

Точка a называется точкой максимума функции f, если существует такая ε-окрестность точки a, что для любого x из этой окрестности выполняется неравенство f (a) ≥ f (x).

Точка a называется точкой минимума функции f, если существует такая ε-окрестность точки a, что для любого x из этой окрестности выполняется неравенство f (a) ≤ f (x).

Точки, в которых достигается максимум или минимум функции, называются точками экстремума.

В точке экстремума происходит смена характера монотонности функции. Так, слева от точки экстремума функция может возрастать, а справа – убывать. Согласно определению, точка экстремума должна быть внутренней точкой области определения.

(x ≠ a) выполняется неравенство f (x) ≤ f (a)

то точка a называется точкой наибольшего значения функции на множестве D:

(x ≠ b) выполняется неравенство f (x) > f (b)

то точка b называется точкой наименьшего значения функции на множестве D.

Точка наибольшего или наименьшего значения может быть экстремумом функции, но не обязательно им является.

Точку наибольшего (наименьшего) значения непрерывной на отрезке функции следует искать среди экстремумов этой функции и ее значений на концах отрезка.

График 1.3.5.1.Функция, ограниченная сверху

График 1.3.5.2.Функция, ограниченная снизу

График 1.3.5.3.Функция, ограниченная на множестве D.

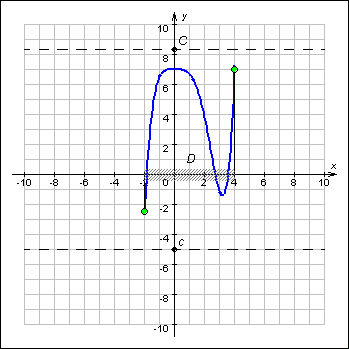
Если существует число C такое, что для любого

выполняется неравенство f (x) ≤ C, то функция f называется ограниченной сверху на множестве D.

Если существует число c такое, что для любого

выполняется неравенство f (x) ≥ c, то функция f называется ограниченной снизу на множестве D.

Функция, ограниченная и сверху, и снизу, называется ограниченной на множестве D. Геометрически ограниченность функции f на множестве D означает, что график функции y = f (x),

лежит в полосе c ≤ y ≤ C.

Если функция не является ограниченной на множестве, то говорят, что она не ограничена.

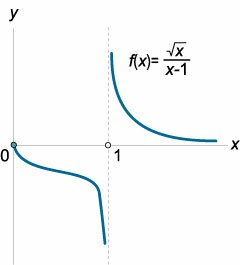
Примером функции, ограниченной снизу на всей числовой оси, является функция y = x2. Примером функции, ограниченной сверху на множестве (–∞; 0) является функция y = 1/x. Примером функции, ограниченной на всей числовой оси, является функция y = sin x.

Источник

Что называется монотонностью функции

Пусть \(y = f\left( x \right)\) является дифференцируемой функцией на интервале \(\left( \right).\) Функция называется возрастающей (или неубывающей ) на данном интервале, если для любых точек \(, \in \left( \right),\) таких, что \( строго возрастающей на интервале \(\left( \right).\)

Аналогично определяются убывающая (или невозрастающая ) и строго убывающая функции.

Если функция \(f\left( x \right)\) дифференцируема на интервале \(\left( \right)\) и принадлежит к одному из четырех рассмотренных типов (т.е. является возрастающей, строго возрастающей, убывающей или строго убывающей), то такая функция называется монотонной на данном интервале.

Снова рассмотрим функцию \(y = f\left( x \right),\) считая ее дифференцируемой на некотором интервале \(\left( \right).\) Возрастание или убывание функции на интервале определяется по знаку первой производной функции.

Поскольку \(f’\left( c \right) \ge 0,\) то правая часть равенства неотрицательна. Следовательно, \[f\left( <> \right) \ge f\left( <> \right).\] т.е. функция \(y = f\left( x \right)\) является возрастающей на интервале \(\left( \right).\)

Рассмотрим теперь случаи строгого возрастания и строгого убывания функции. Здесь существует похожая теорема, описывающая необходимые и достаточные условия. Опуская доказательство, сформулируем ее для случая строго возрастающей функции.

\(f’\left( x \right) \ge 0\;\forall\;x \in \left( \right);\)

Производная \(f’\left( x \right)\) тождественно не равна нулю ни в каком промежутке \(\left[ <,> \right] \in \left( \right).\)

Условие \(1\) содержится в теореме \(1\) и является признаком неубывающей функции. Дополнительное условие \(2\) требуется для того, чтобы исключить участки постоянства функции, в которых производная функции \(f\left( x \right)\) тождественно равна нулю.

На практике (при нахождении интервалов монотонности) обычно используется достаточное условие строгого возрастания или строгого убывания функции. Из теоремы \(2\) следует такая формулировка достаточного признака:

Соответственно, условие \(f’\left( x \right) строго убывающую функцию.

Число точек, в которых \(f’\left( x \right) = 0,\) является, как правило, конечным. Согласно теореме \(2\), они не могут плотно заполнять какой-либо промежуток в интервале \(\left( \right).\)

Приведем также признак строгого возрастания (убывания) функции в точке:

Если \(f’\left( <> \right) > 0\), то функция \(f\left( x \right)\) строго возрастает в точке \(\);

Если \(f’\left( <> \right) сумма функций \(f + g\) также возрастает (убывает) на этом интервале.

Если функция \(f\) возрастает (убывает) на интервале \(\left( \right),\) то противоположная функция \(-f\) убывает (возрастает) на этом интервале.

Если функция \(f\) возрастает (убывает) на интервале \(\left( \right),\) то обратная функция \(\large\frac<1>\normalsize\) убывает (возрастает) на этом интервале.

Если функции \(f\) и \(g\) возрастают (убывают) на интервале \(\left( \right)\) и, кроме того, \(f \ge 0\), \(g \ge 0\), то произведение функций \(fg\) также возрастает (убывает) на этом интервале.

Если функция \(g\) возрастает (убывает) на интервале \(\left( \right),\) а функция \(f\) возрастает (убывает) на интервале \(\left( \right),\) где \(g:\left( \right) \to \left( \right),\) то композиция функций \(f \circ g\) (т.е. сложная функция \(y = f\left( \right)\) также возрастает (убывает) на интервале \(\left( \right).\)

Данная функция является суммой функций \(\) и \(3.\)

Первую функцию \(\) можно рассматривать как произведение двух одинаковых функций \(\). Из примера \(1\) следует, что квадратичная функция \(\) строго возрастает при \(x \ge 0.\) Следовательно, функция \(\) также строго возрастает при \(x \ge 0\) на основании свойства \(4\).

Второе слагаемое \(3\) представляет собой трехкратную сумму функций \(\) и, поэтому, также является строго возрастающей (на основании свойства \(1\)).

Итак, исходная функция \(f\left( x \right) = + 3\) является суммой двух строго возрастающих функций и, следовательно, также строго возрастает при \(x \ge 0.\)

Для контроля рассмотрим также неравенство \(f’\left( x \right) Рис.5

Следовательно, на основании достаточного признака монотонности, функция строго возрастает при \(x \in \left( <\large\frac<1>\normalsize,\infty > \right)\) и строго убывает при \(x \in \left( <0, \large\frac<1>\normalsize> \right).\) Ее вид схематически приведен на рисунке \(10\).

На основании достаточного признака монотонности заключаем, что функция возрастает при \(x \in \left( <0,\large\frac<1><2>\normalsize> \right)\) и убывает при \(x \in \left( <\large\frac<1><2>\normalsize,1> \right).\) График функции представляет собой полуокружность с центром в точке \(\left( <\large\frac<1><2>\normalsize,0> \right)\) и радиусом \(<\large\frac<1><2>\normalsize>\) (рисунок \(14\)).

Источник

Монотонность

Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательно, либо всегда неположительно. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной.

Содержание

Определения

Пусть дана функция 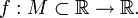Тогда

(Строго) возрастающая или убывающая функция называется (строго) монотонной.

Другая терминология

Иногда возрастающие функции называют неубыва́ющими, а убывающие функции невозраста́ющими. Строго возрастающие функции тогда зовут просто возрастающими, а строго убывающие просто убывающими.

Свойства монотонных функций

Условия монотонности функции

Обратное, вообще говоря, неверно. Производная строго монотонной функции может обращаться в ноль. Однако, множество точек, где производная не равна нулю, должно быть плотно на интервале (a,b). Точнее имеет место

Аналогично, f строго убывает на интервале (a,b) тогда и только тогда, когда выполнены следующие два условия:

Примеры

См. также

Полезное

Смотреть что такое «Монотонность» в других словарях:

монотонность — однообразие, однообразность, одинаковость, однотонность, одноцветность; размеренность, усыпительность, однозвучность, нудность, одноликость. Ant. разнообразие, многоцветность, неоднородность Словарь русских синонимов. монотонность 1. однотонность … Словарь синонимов

МОНОТОННОСТЬ — свойство некоторых видов труда, требующих от человека длительного выполнения однообразных действий или непрерывной и устойчивой концентрации внимания в условиях дефицита сенсорных нагрузок. На многих предприятиях используются станки с ЧПУ и… … Российская энциклопедия по охране труда

МОНОТОННОСТЬ — (греч., от monos один, и phone звук). Однообразие звуков. Недостаток модуляции при говоре и пении; вообще однообразие (в жизни, стиле и т. п.). Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. МОНОТОННОСТЬ греч., от … Словарь иностранных слов русского языка

монотонность — МОНОТОННОСТЬ, однозвучность, однотонность МОНОТОННЫЙ, однозвучный, однотонный МОНОТОННО, однозвучно, однотонно … Словарь-тезаурус синонимов русской речи

монотонность — МОНОТОННЫЙ, ая, ое; онен, онна. Однообразный по тону, интонации. Монотонное пение. М. голос. Монотонная жизнь (перен.: лишённая разнообразия). Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

МОНОТОННОСТЬ — (monotonicity) Свойство, обладая которым линии либо функции, либо никогда не убывают, либо никогда не возрастают. В частности, этот термин используется применительно к электоральной системе либо к системе пропорционального распределения. Это… … Политология. Словарь.

Монотонность — ж. отвлеч. сущ. по прил. монотонный Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой

монотонность — монотонность, монотонности, монотонности, монотонностей, монотонности, монотонностям, монотонность, монотонности, монотонностью, монотонностями, монотонности, монотонностях (Источник: «Полная акцентуированная парадигма по А. А. Зализняку») … Формы слов

МОНОТОННОСТЬ — (от греч. μονότονος – однотонный) – свойство нек рых логических или математических операций (функций), состоящее, грубо говоря, в том, что направление возможного изменения результата операций зависит только от направления изменения того, над чем… … Философская энциклопедия

Источник