Что называется модулем кручения

Большая Энциклопедия Нефти и Газа

Модуль кручения при комнатной температуре колеблется от 9 000 кг мм2 до 22000 кг мм2 и медленно понижается с ростом температуры до 1000 К. При дальнейшем повышении температуры значение модуля кручения падает быстрее, достигая 3 06Э кг мм2 при 2 000 К. Образование тонких пленок окислов на вольфраме и их восстановление в водороде представляют значительный интерес для конструкторов электровакуумных приборов. [2]

Модуль кручения и твердость весьма заметным образом изменяются в зависимости от кристалличности полиэтилена. [4]

Модуль кручения G представляет собой меру жесткости материала. Заметим, что более кристаллический образец является более жестким во всей области температур, охватываемых опытом. [6]

Экспериментально модуль кручения можно измерить, наблюдая крутильные колебания тяжелого тела, подвешенного к нижнему концу проволоки. [7]

Экспериментально модуль кручения D проволоки можно измерить при помощи крутильных колебаний тяжелого тела, подвешенного к ее концу. [9]

Таким образом, модуль кручения кривой равен скорости вращения соприкасающейся плоскости. [10]

Проанализировать характер кривой зависимости модуля кручения от температуры при заданном моменте инерции системы; определить температурные области переходов полимеров из одного физического состояния в другое; проанализировать полученную зависимость тангенса угла механических потерь от температуры при заданном моменте инерции системы; объяснить смещение температур стеклования полимеров при изменении момента инерции системы. [14]

Источник

МОДУЛЬ КРУЧЕНИЯ

При закручивании стержня вокруг его оси возникающая деформация является неоднородной деформацией сдвига. Это делается очевидным, если мысленно разбить стержень на ряд коаксиальных полых цилиндров. Угол сдвига g одного такого полого цилиндра (внутренним радиусом r и толщиной стенки dr) связан с углом закручивания j очевидным соотношением (см. рис. П1):

(П1).

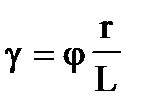
Полученное соотношение показывает, что сдвиг является неоднородным, т.к. угол сдвига g зависит от расстояния до оси r.

Деформация стержня приводит к возникновению упругих сил в стержне, момент которых нетрудно вычислить. Согласно закону Гука напряжение s при сдвиге связано с углом сдвига g и модулем сдвига G соотношением:

Поэтому момент упругих сил (момент вычисляется относительно оси цилиндра), возникающих в рассматриваемом цилиндре, равен:

С учетом (П1) и (П2) dM запишется в виде:

(П4).

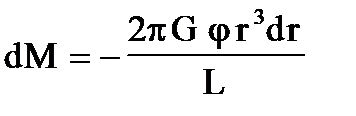
Интегрируя (П4) по dr получим:

(П5).

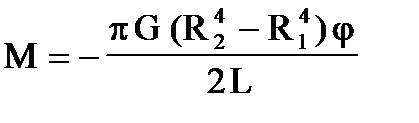
R 4 ). Это позволяет использовать трубы вместо стержней практически не теряя в прочности конструкции. Действительно, даже если R₂/R₁=1,5, то (R₂/R₁) 4 »6, и такая труба будет менее жесткой, чем сплошной стержень всего на 15%, масса же такой трубы будет приблизительно вдвое меньше, чем у сплошного стержня.

Коэффициент перед (в (П5) называется модулем кручения:

(П6).

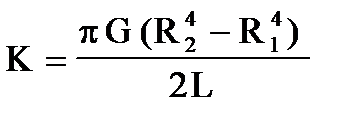
В нашем опыте мы используем проволоку, поэтому (П6) принимает вид:

(П7).

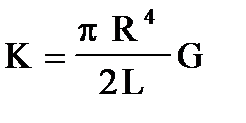
Рассмотрим тело с моментом инерции I, подвешенное на проволоке с модулем кручения K. Если телу сообщить вращение вокруг оси на угол j, то это приведет к возникновению в проволоке упругих сил с моментом

Запишем уравнение моментов для тела:

(П8).

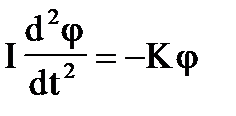
Поделив обе стороны этого уравнения ни I, придем к уравнению гармонических колебаний:

(П9).

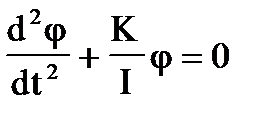
Квадрат частоты колебаний, как известно, дается коэффициентом перед j:

(П10).

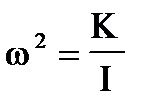
С учетом равенства (П7), получаем для периода колебаний T=2p/w:

(П11).

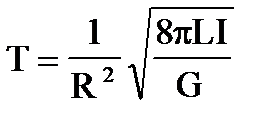
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Определение модулей кручения и сдвига методом крутильных колебаний

Министерство образования республики Беларусь

Белорусский национальный технический

Методические указания к лабораторной работе № 23

Определение модулей кручения и сдвига методом крутильных колебаний

для студентов строительных специальностей

УДК 531.38(076.5)

В работе изложен экспериментальный метод определения модуля кручения и модуля сдвига упругого материала в виде струны методом крутильных колебаний. Рассмотрены оценки модуля Юнга и модуля всестороннего сжатия исследуемого материала.

© Белорусский национальный технический университет, 2006

Цель работы: 1. Определить методом крутильных колебаний модули кручения и сдвига струны.

2. Получить оценки численных значений модуля Юнга и модуля всестороннего сжатия материала струны.

1. Упругие свойства твердых тел.

В теории упругости изучают действия только статических нагрузок на твердые тела. Динамические нагрузки представляют собой волны в телах.

Под влиянием внешних статических силовых (не температурных) воздействий тела испытывают деформацию, т. е. меняют форму и размеры. В линейной теории упругости изучают только малые напряжения (нагрузки).

Рассмотрим следующие виды деформаций: сжатие (растяжение), сдвиг, всестороннее сжатие, кручение.

а) Для продольных упругих деформаций изотропных твердых тел (стержней, струн) справедлив закон Гука: относительная деформация e пропорциональна напряжению s:

, (1)

где – напряжение, т. е. внешняя сила F отнесенная к единице площади поперечного сечения тела (стержня), – относительная деформация тела, т. е. отношение абсолютной деформации к начальной длине тела (стержня) , l – длина после нагрузки; Е – модуль продольной упругости или модуль Юнга.

Модуль Юнга – числено равен напряжению при относительной деформации равной единице.

б) Сдвиг – деформация, при которой все плоские слои твердого тела, параллельные некоторой закрепленной плоскости (плоскости сдвига) смещаются параллельно друг другу не искривляясь и не изменяясь в размерах. Сдвиг происходит под действием силы F, приложенной к грани параллельной плоскости сдвига (рис.1).

Мерой деформации является угол сдвига , измеряемый в радианах.

По закону Гука: относительный сдвиг q пропорционален касательному (скалывающему) напряжению , т. е.

q. (2)

Здесь модуль сдвига численно равен касательному напряжению, вызывающему относительный сдвиг, равный единице.

Относительное продольное растяжение (сжатие) тела сопровождается его относительным сужением (расширением) , где d – поперечный размер тела.

Коэффициентом Пуассона (модулем поперечного сжатия) m называется отношение относительного поперечного сужения (расширения) к относительному продольному удлинению (сжатию) , т. е.

. (3)

Из теоретических соображений [1,7] коэффициент Пуассона m заключен в пределах

Материалы с отрицательным m неизвестны. Для большинства твердых тел из опыта m » 0,25.

в) Деформация всестороннего сжатия (растяжения) – уменьшение (увеличение) объема тела без изменения его формы под влиянием равномерно распределенных по всей поверхности тела сжимающих (растягивающих) сил.

По закону Гука имеем:

, (4)

где – относительное изменение объема тела под действием напряжения s.

Здесь модуль всестороннего сжатия (объемной упругости) численно равен напряжению при относительном изменении объема равном единице.

Из теории упругости [1,7] вытекают следующие связи модулей G, E, K [1,7]

(5)

(6)

г) Кручением называются деформация тела (струны) с одним закрепленным концом под действием пары сил, плоскость которой перпендикулярна к оси тела. Момент М этой пары сил называется крутящим (вращательным) моментом.

Для цилиндрической формы (струны, стержня) по закону Гука угол закручивания j отнесенный к длине струны L, т. е. относительная деформация пропорциональна крутящему моменту М, т. е.

(7)

Модуль кручения численно равен вращательному моменту при относительном угле закручивания равном единице.

Для анизотропных твердых тел напряжения и деформации являются тензорами второго ранга [4].

В декартовых координатах тензор напряжений равен

,

тензор деформаций .

Эти тензоры линейно связаны между собой.

Для анизотропных кристаллов закон Гука принимает вид

,

где i, j, k, l = 1, 2, 3 и по повторяющимся индексам предполагается суммирование. Число модулей упругости тензора сводятся к 21 в виду симметрии тензора и [4]. В самом простейшем изотропном случае получается только два модуля Е и G.

2. Связь модуля сдвига с модулем кручения струны

При закручивании струны ее нижний торец испытывает сдвиг относительно верхнего [2]. Прямая ВА поворачивается, занимая положение ВА’. Угол q является углом сдвига. По формуле (2) угол сдвига q равен

, (8)

где st – касательное усилие, приложенное к элементу поверхности dS, расположенному у точки А¢ (см. Рис.3), а G – модуль сдвига.

. (9)

Тогда из (8) и (9) имеем

. (10)

Сила, приложенная к элементу поверхности dS, равна , а ее момент .Элемент поверхности dS в полярных координатах r, q равен , откуда

или с учетом (9) найдем

(11)

Полный момент, приложенный ко всему нижнему торцу получается интегрированием (11) по всей площади круга радиуса r:

. (12)

. (13)

Сравнивая (13) и (7) получаем для модуля кручения

, (14)

Из соотношения (13) угол закручивания j зависит от модуля сдвига G и обратно пропорционален радиусу струны, взятому в четвертой степени.

3. Крутильные колебания

В данной работе используется крутильный маятник, представляющий собой рамку с телом, жестко соединенную с натянутой стальной струной, закрепленной на обеих концах с установкой.

При выведении рамки с телом из положения равновесия на некоторый угол j создается возвращающий момент силы

, (15)

где коэффициент D – это модуль кручения, множитель 2 в соотношении (15) учитывает наличие двух струн, на которых закреплена рамка. Знак «минус» означает, что крутящий момент возвращает рамку в положение равновесия.

На протяжении времени в несколько периодов трением (сопротивлением) можно пренебречь и крутильные колебания будут незатухающими.

Основное уравнение динамики вращательного движения твердого тела с учетом (15) примет вид

. (16)

Здесь I – момент инерции рамки с телом относительно оси вращения.

Уравнение (16) записывается в стандартной форме

(17)

. (18)

Из уравнения (17) следует, что крутильные колебания в отсутствии трения будут гармоническими

. (19)

Амплитуда jm и начальная фаза j0 определяются из начальных условий.

частота свободных незатухающих колебаний равна

. (20)

Период колебаний рамки с телом с учетом (20) равен

. (21)

Из соотношения (21) вытекает формула для определения модуля кручения

. (22)

Соотношение (22) позволяет по измеренному периоду Т колебаний и известному моменту инерции I вычислить модуль кручения D. Из формулы (14) можно вычислить модуль сдвига G материала струны:

. (23)

4. Оценка модуля Юнга и модуля всестороннего сжатия.

Формулы (5) и (6) позволяют получить численные значения модуля Юнга Е и модуля всестороннего сжатия К. Для этого необходимо знать коэффициент Пуассона m. Как следует из таблицы 1 упругих свойств многих металлов и их сплавов [5] коэффициент Пуассона в среднем равен

. (24)

Этот коэффициент m используется в формулах (5) и (6) при оценке модулей Е и К.

Источник

ЛАБОРАТОРНАЯ РАБОТА №104

Цель работы: Экспериментальное определение модуля кручения и модуля сдвига стальной проволоки методом крутильных колебаний.

Приборы и принадлежности: крутильный маятник, секундомер, штангенциркуль, измерительная линейка, технические весы.

Теоретическое введение

Как показывает опыт, при воздействии на тело внешних сил оно меняет форму и размеры, т.е. наблюдается механическая деформация. В физике рассматриваются наиболее простые виды деформации: растяжение, сжатие, изгиб, сдвиг, кручение.

Пусть имеем тело в форме прямоугольного параллелепипеда, закрепленного в своей нижней части, и мысленно разделим его на ряд слоев, параллельных основанию (рис.1). Если к верхней плоскости параллелепипеда приложить силу , касательную к этой плоскости, то тело деформируется – одни слои будут двигаться относительно других, оставаясь параллельными друг другу, причем, боковые грани параллелепипеда останутся плоскостями, параллельными друг другу. Такая деформация является чистым сдвигом и характеризуется углом сдвига j

,

где d – толщина тела, а bb / – абсолютная величина сдвига верхнего слоя относительно нижнего.

,

Если угол j мал, то tg j = j = , угол сдвига, j называют относительным сдвигом, выражаемым в радианах. По закону Гука относительный сдвиг j пропорционален касательному напряжению τ:

где G – модуль сдвига, [ Н/м 2 ] . Модуль сдвига равен касательному напряжению, необходимому для изменения угла сдвига на единицу ( j =1). Модуль сдвига зависит от рода, температуры и кристаллической структуры вещества.

Перейдем далее к деформации кручения. Рассмотрим образец в виде цилиндрического стержня длиной L и радиусом r (рис.2). Пусть нижнее основание образца закреплено неподвижно, а к верхнему приложен момент пары сил , закручивающий верхний конец образца против часовой стрелки.

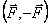
Момент пары сил, вызывающий кручение стержня, называется крутящим моментом. Для небольших деформаций любого типа справедлив закон Гука, поэтому применительно к кручению можно записать:

где модуль кручения D равен моменту сил, вызывающему закручивание стержня на единичный угол. [ D ] =Н × м.

Поскольку деформация кручения представляет собой одновременные действия сдвига и сжатия (или растяжения), то между модулем кручения D и сдвига G существует количественная связь, которую можно определить следующим образом.

и

Тогда касательная сила, действующая на поверхность кольца, равна

где dS =2π rdr – площадь поверхности кольца. С учетом (4) и (5) можно записать в виде:

Момент этой силы относительно оси равен:

Тогда момент сил по всей поверхности диска равен:

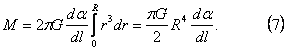
Поскольку стержень однородный, то деформация кручения однородная и для нее справедливо соотношение:

С учетом (8) уравнение (7) можно записать в виде:

Сравнивая (9) с формулой (2), получим:

Если осуществлять крутящий момент поворотом вокруг оси цилиндра ОО / какой-либо значительной массы, прикрепленной к свободному концу стержня, то согласно основному уравнению динамики вращательного движения можно записать:

(11)

где J – момент инерции вращающейся массы, d 2 a / dt 2 – ее угловое ускорение.

Из формул (2) и (11) имеем:

Обозначив 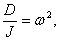получим

Из (13) находим модуль кручения:

Описание рабочей установки и метода измерений

Для определения модуля кручения и модуля сдвига используется крутильный маятник. К нижнему концу вертикально висящей проволоки 1 крепится горизонтально висящий стержень 2 со средним грузом 3 и двумя равными грузами 4, массой m каждый, которые можно перемещать вдоль стержня 2 (рис.4). Если сообщить этой системе небольшой импульс в плоскости, перпендикулярной оси проволоки, то система начнет совершать крутильные колебания, при которых проволока закручивается то в одну, то в другую сторону. Такое устройство и является крутильным маятником.

Устанавливают каждый из грузов 4 сначала на расстоянии l ₁ от оси вращения, а потом на расстоянии l ₂ и определяют периоды колебаний системы Т ₁ и Т₂. Тогда согласно формуле (13) для этих величин можно записать:

и ,

где J₁ и J₂ – моменты инерции всех тел системы относительно осей, проходящих через центр масс каждого тела.

Найдя разность и составив пропорцию с учетом (15):

,

Подставляя (16) в (14), получим:

где L – длина проволоки, R – ее радиус.

1. Расположить подвижные грузы на минимальном расстоянии от оси вращения крутильного маятника. Измерить расстояние l ₁ от оси маятника до центра подвижного груза.

2. Закручивают маятник на малый угол (не более 6 0 ) относительно оси проволоки, после чего предоставляют его самому себе. Маятник начинает совершать колебания в горизонтальной плоскости. Секундомером измерить время t ₁ 30-50 полных колебаний. Опыт повторяют не менее 5 раз с одним и тем же выбранным числом колебаний. Находят среднее значение >. Определить период колебаний:

где n – число колебаний маятника.

4. Раздвинуть подвижные грузы на максимальное расстояние от оси маятника. Измерить расстояние l ₂ от оси маятника до центра подвижного груза.

8. По формуле (18) определить модуль сдвига материала проволоки. Длина проволоки L = 1,82 м.

10. Данные результатов измерений и вычислений занести в таблицу.

Источник