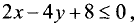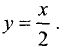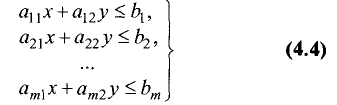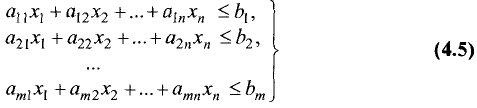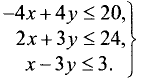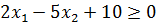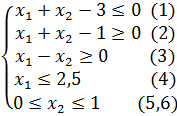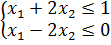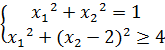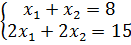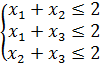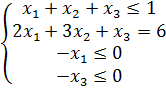Что называется множеством точек

Выпуклые множества точек и их свойства с примерами решения и образцами выполнения

Основные определения:

Множество точек называется выпуклым, если оно вместе с любыми
двумя своими точками содержит весь отрезок, соединяющий эти точки.

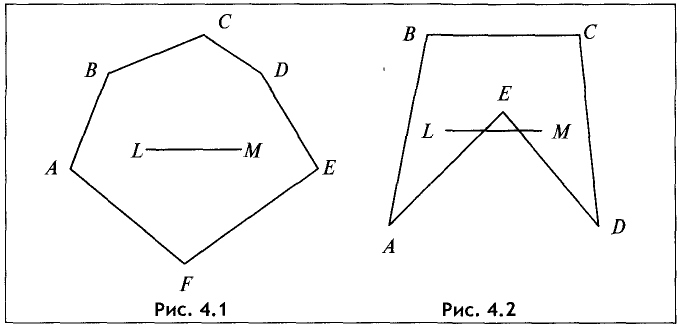
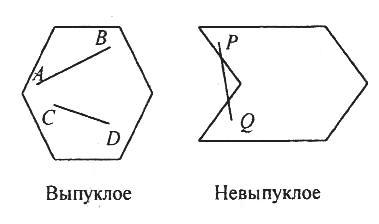
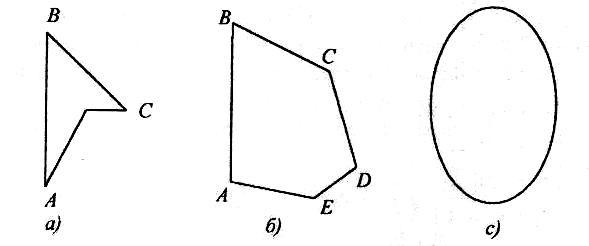
Например, многоугольник, представленный на рис. 4.1,
является выпуклым, а многоугольник на рис.4.2 выпуклым не является.

Выпуклыми множествами могут быть не только многоугольники. Примерами выпуклых множеств являются прямая, круг, куб,
многогранная область, полуплоскость, полупространство и т.д.

Пересечение любого числа выпуклых множеств есть выпуклое
множество.

Точка множества называется внутренней, если в любой ее окрестности (например, круг или шар с центром в этой точке) содержатся точки только данного множества.

Точка множества называется граничной, если в любой ее окрестности содержатся как точки, принадлежащие данному множеству, так и точки, не принадлежащие ему.

Точка множества называется угловой (крайней), если она не является внутренней ни для какого отрезка, целиком принадлежащего данному множеству.

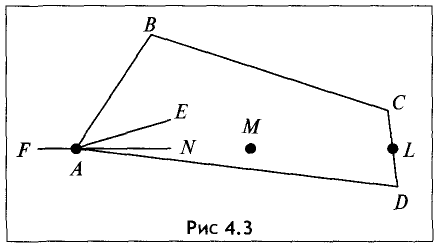
Примеры угловой А, внутренней L и граничной М точек приведены на рис. 4.3.

Точка А является угловой, так как для любого отрезка АЕ,
целиком принадлежащего многоугольнику, она не является
внутренней. Точка А — внутренняя для отрезка FN, но этот отрезок не принадлежит целиком множеству.

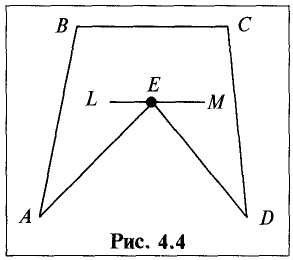
Для выпуклого множества угловые точки всегда совпадают с вершинами многоугольника (многогранника).

Так, на рис. 4.4 точка Е является вершиной невыпуклого многоугольника, но не является угловой, так как она является внутренней для отрезка LM, целиком принадлежащего этому
многоугольнику.

Множество точек называется замкнутым, если оно включает все свои граничные точки.

Множество точек называется ограниченным, если существует круг (шар) радиуса конечной длины с центром в любой точке множества, который полностью содержит в себе данное множество. В противном случае множество называется неограниченным.

Выпуклое замкнутое множество точек плоскости (пространства), имеющее конечное число угловых точек, называется выпуклым многоугольником (многогранником), если оно ограниченное, и выпуклой многоугольной (многогранной) областью, если оно неограниченное.

Введенные понятия рассматривались для множества точек на
плоскости и в пространстве. Их можно обобщить также на n-мерное
точечное пространство.

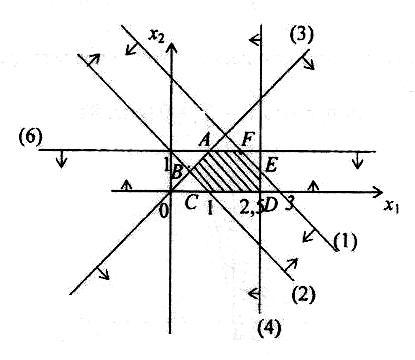
Геометрический смысл решений неравенств

Рассмотрим решения неравенств с двумя переменными типа

Теорема:

Множество решений неравенств с двумя переменными (4.1) является одной из двух полуплоскостей, на которые вся плоскость делится прямой

включая и эту прямую, а другая полуплоскость — множеством решений неравенства

Пример:

Построить график множества решений следующих
неравенств:

Решение:

В соответствии с теоремой множество решений
приведенных неравенств есть полуплоскость.

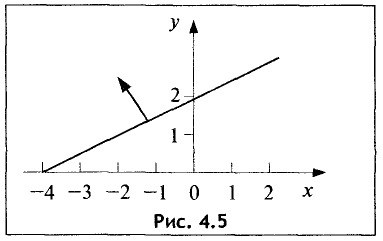
1.Границей первой полуплоскости является прямая

Представим уравнение этой прямой в виде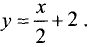
Ее график представлен на рис. 4.5.

Для определения искомой полуплоскости зададим произвольную контрольную точку, не лежащую на построенной прямой. Проще всего задать точку с координатами (0; 0). Подставив данные
координаты в неравенство

видим, что оно не выполняется, так как 8 > 0. Поэтому искомой является верхняя полуплоскость.

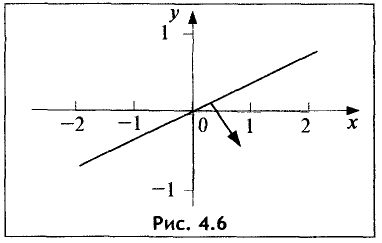
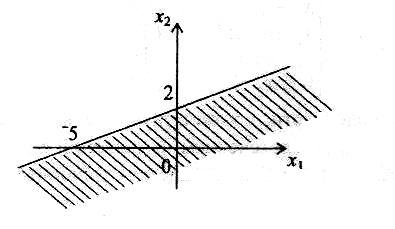
2.Границей второй полуплоскости является прямая

Представим это уравнение в виде

График исследуемой прямой представлен на рис. 4.6.

В данном случае точка с координатами (0; 0) лежит на этой
прямой. Поэтому выбираем точку с координатами (0; —1) и подставляем данные координаты в неравенство 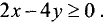Так как неравенство выполняется (4 > 0), то искомой является нижняя полуплоскость. ►

Основные свойства выпуклого множества точек

Рассмотрим множество решений совместной системы линейных
неравенств с двумя переменными.

Теорема:

Множество решений совместной системы т линейных
неравенств с двумя переменными

является выпуклым многоугольником (или выпуклой многоугольной областью).

Знаки некоторых или всех неравенств могут быть

Эту теорему для n переменных можно сформулировать
следующим образом.

Теорема:

Множество решений совместной системы m линейных
неравенств с n переменными

является выпуклым многогранником (или выпуклой многогранной областью) в n-мерном пространстве.

Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью решения системы.

Область решений системы, удовлетворяющая условиям неотрицательности 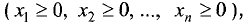называется областью неотрицательных (или допустимых) решений.

Пример:

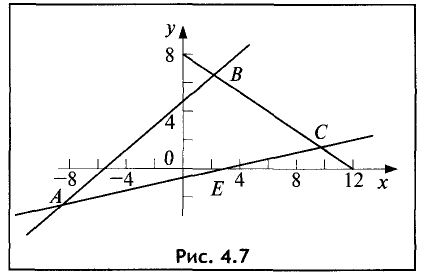
Построить область решений и область допустимых
решений системы неравенств и определить координаты угловых точек области допустимых решений:

Решение:

Областью решений является треугольник ABC, представленный на рис. 4.7.

Для нахождения искомой полуплоскости зададим контрольную
точку с координатами (0; 0). Подставив данные координаты в неравенство 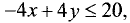видим, что оно выполняется, так как 0

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Точечные множества

Множества, элементами которых являются точки, называются точечными множествами. Таким образом, можно говорить о точечных множествах на прямой, на плоскости, в каком-либо пространстве. Ради простоты мы ограничимся рассмотрением точечных множеств на прямой.

Между действительными числами и точками на прямой имеется тесная связь: каждому действительному числу можно отнести точку на прямой и обратно. Поэтому, говоря о точечных множествах, мы будем причислять к ним и множества, состоящие из действительных чисел — множества на числовой прямой. Обратно: для того чтобы задать точечное множество на прямой, мы будем обычно задавать координаты всех точек нашего множества.

Точечные множества (и, в частности, точечные множества на прямой) обладают рядом особых свойств, отличающих их от произвольных множеств и выделяющих теорию точечных множеств в самостоятельную математическую дисциплину. Прежде всего имеет смысл говорить о расстоянии между двумя точками. Далее, между точками на прямой можно установить соотношения порядка (левее, правее); в соответствии с этим говорят, что точечное множество на прямой является упорядоченным множеством. Наконец, как уже отмечалось выше, для прямой справедлив принцип Кантора; это свойство прямой принято характеризовать как полноту прямой.

Введем обозначения для простейших множеств на прямой.

Начнем с рассмотрения различных возможностей расположения множества в целом на прямой.

Ограниченные и неограниченные множества

Нетрудно видеть, что если — фиксированная точка на прямой, то множество будет ограничено в том и только в том случае., если расстояния от точки до любой точки не превосходят некоторого положительного числа.

Множества, ограниченные сверху и снизу

Ясно, что данное выше определение ограниченного множества эквивалентно следующему: множество точек на прямой называется ограниченным, если оно ограничено сверху и снизу. Несмотря на то, что эти два определения очень похожи друг на друга, между ними имеется существенное различие: первое основано на том, что между точками на прямой определено расстояние, а второе, что эти точки; образуют упорядоченное множество.

Верхняя и нижняя грань множества

Расположение точечного множества вблизи какой-либо точки на прямой

Укажем несколько примеров, поясняющих все эти понятия.

Пример 1. Пусть множество состоит из точек с координатами

Пример 4. Пусть множество состоит из всех точек с целыми координатами на прямой. Каждая точка является его изолированной точкой; множество не имеет предельных точек.

Теорема Больцано-Вейерштрасса

Всякое ограниченное бесконечное множество точек на прямой имеет хотя бы, одну предельную точку.

Источник

Выпуклые множества точек

Определение 1. Множество точек плоскости или трехмерного пространства называется выпуклым, если любые две точки этого множества можно соединить отрезком прямой, полностью лежащим в данном множестве (см. рис.6).

Рисунок 6 – Изображение множеств

Теорема 1. Пересечение конечного числа выпуклых множеств является выпуклым множеством.

Определение 2. Точка множества называется внутренней, если существует сколь угодно малая ее окрестность, содержащая только точки данного множества.

Определение 3. Точка множества называется граничной, если любая ее окрестность содержит как точки, принадлежащие данному множеству, так и не принадлежащие ему (см. рис. 7).

Определение 4. Граничная точка выпуклого множества называется угловой, если через нее можно провести отрезок, все точки которого не принадлежат данному множеству (см. рис. 7).

Различные по форме множества могут иметь конечное или бесконечное количество угловых точек.

Рисунок 7 – Изображение точек множества

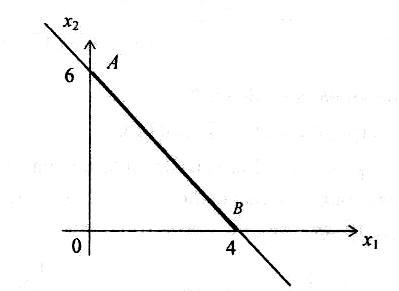
Пример 1. Определить угловые точки множества, заданного условиями .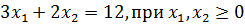

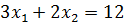
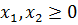
Решение. Уравнение имеет бесчисленное множество решений – множество точек, лежащих на прямой. А условие определяет точки этой прямой, лежащие только в. первой четверти координатной плоскости (рис. 8).

Множество точек отрезка АВ представляет собой выпуклое множество допустимых решений с двумя угловыми точками А(0;6)и В(4;0).

Рисунок 8 – решение примера 1

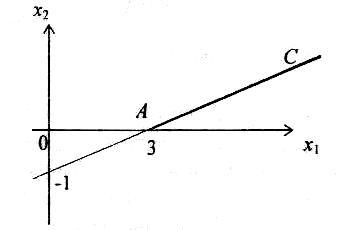
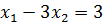
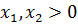
Пример 2. Определить угловые точки множества: , при .

Решение. Множество допустимых решений – луч АС.

Здесь лишь одна угловая точка A (3,0) соответствует единственному допустимому базисному решению (см. рис. 9).

Рисунок 9 – решение примера 2

Как правило, система ограничений в задачах математического программирования представлена в виде системы неравенств, решение каждого из которых занимает определенную часть плоскости (пространства).

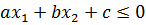
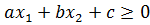
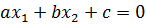
Теорема 2. Решением неравенства или является одна из полуплоскостей, на которые прямая делит всю координатную плоскость.

Пример 3. Построить множество точек, удовлетворяющих неравенству

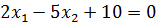
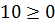
Решение. Строим прямую (рис. 10). Она разбила всю плоскость на две полуплоскости, одна из которых и является решением неравенства. Для проверки выберем точку О (0; 0) и ее координаты подставим в исходное неравенство. Получим истинное неравенство . Следовательно, полуплоскость, содержащая начало координат, и является решением.

Рисунок 10 – решение примера 3

Пример 4. Построить множество точек, удовлетворяющих неравенству .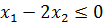

Решение. Строим прямую 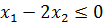(рис. 11).

Рисунок 11 – решение примера 4

Прямая разделила всю плоскость на две полуплоскости, одна из которых и является решением неравенства. Для проверки выберем, например, точку А (4; 1) и ее координаты подставим в исходное неравенство. Получим ложное неравенство 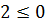. То есть полуплоскость, содержащая точку А (4; 1), не является решением. Следовательно, решением является другая полуплоскость, не содержащая этой точки.

Замечание. Для того чтобы найти множество точек, удовлетворяющих системе линейных неравенств, необходимо решить каждое из неравенств и затем найти пересечение этих решений.

Пример 5. Построить множество точек, удовлетворяющих системе неравенств:

Рисунок 12 – решение примера 5

Задачи для самостоятельного решения

1. Какие из множеств, изображенных на рис. 13, являются выпуклыми?

Рисунок 13 – Изображение множеств

2. Проверить, будут ли выпуклыми данные множества:

б) круг

в) сфера ;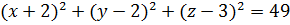

г) отрезок и точка, лежащая вне этого отрезка на плоскости;

д) два отрезка, имеющие одну общую точку;

е) два треугольника, имеющие одну общую точку/

3. Выяснить, будут ли выпуклы данные множества. Найти угловые точки данных множеств:

а)

б)

в)

5. Найти вершины многогранных множеств, ограничения для которых приведены в условиях:

а)

б)

в)

г)

Источник

Замкнутые и открытые множества

Одна из основных задач теории точечных множеств — изучение свойств различных типов точечных множеств. Познакомимся с этой теорией на двух примерах и изучим свойства так называемых замкнутых и открытых множеств.

Приведем примеры замкнутых и открытых множеств. Всякий отрезок есть замкнутое множество, а всякий интервал — открытое множество. Несобственные полуинтервалы и замкнуты, а несобственные интервалы и открыты. Вся прямая является одновременно и замкнутым и открытым множеством. Удобно считать пустое множество тоже одновременно замкнутым и открытым. Любое конечное множество точек на прямой замкнуто, так как оно не имеет предельных точек. Множество, состоящее из точек

Наша задача состоит в том, чтобы выяснить, как устроено произвольное замкнутое или открытое множество. Для этого нам понадобится ряд вспомогательных фактов, которые мы примем без доказательства.

1. Пересечение любого числа замкнутых множеств замкнуто.

2. Сумма любого числа открытых множеств есть открытое множество.

3. Если замкнутое множество ограничено сверху, то оно содержит свою верхнюю грань. Аналогично, если замкнутое множество ограничено снизу, то оно содержит свою нижнюю грань.

4. Если множество замкнуто, то его дополнение открыто и обратно.

Предложение 4 показывает, что между замкнутыми и открытыми множествами имеется весьма тесная связь: одни являются дополнениями других. В силу этого достаточно изучить одни замкнутые или одни открытые множества. Знание свойств множеств одного типа позволяет сразу выяснить свойства множеств другого типа. Например, всякое открытое множество получается путем удаления из прямой некоторого замкнутого множества.

В силу предложения 4, отсюда сразу вытекает, что всякое открытое множество на прямой представляет собой не более чем счетную сумму непересекающихся интервалов. В силу предложений 1 и 2, ясно также, что всякое множество, устроенное, как указано выше, действительно является замкнутым (открытым).

Как видно из нижеследующего примера, замкнутые множества могут иметь весьма сложное строение.

Канторово совершенное множество

Рассмотрим некоторые свойства этого множества. Множество замкнуто, так как оно образуется путем удаления из прямой некоторого, множества непересекающихся интервалов. Множество не пусто; во всяком случае в нем содержатся концы всех выброшенных интервалов.

Можно показать, что множество имеет мощность континуума. В частности, отсюда следует, что канторово совершенное множество содержит, кроме концов смежных интервалов, еще и другие точки. Действительно, концы смежных интервалов образуют лишь счетное множество.

Разнообразные типы точечных множеств постоянно встречаются в самых различных разделах математики, и знание их свойств совершенно необходимо при исследовании многих математических проблем. Особенно большое значение имеет теория точечных множеств для математического анализа и топологии.

Исследования Н.Н. Лузина и его учеников показали, что имеется глубокая связь между дескриптивной теорией множеств и математической логикой. Трудности, возникающие при рассмотрении ряда задач дескриптивной теории множеств (в частности, задач об определении мощности тех или иных множеств), являются трудностями логической природы. Напротив, методы математической логики позволяют более глубоко проникнуть в некоторые вопросы дескриптивной теории множеств.

Источник

Что называется множеством точек

Линейное программирование – это наука о методах исследования и отыскания наибольшего и наименьшего значений линейной функции, на неизвестное которой наложены линейные ограничения.

Пусть нам задана линейная функция F относительно переменных :

Возьмём c : F ( x )= c (3)

Определение : Гиперповерхность F ( x )= c называется гиперповерхностью равных значений линейной формы

F ( x )= c ₁

F ( x )= c ₂

Определение: Множество точек называется выпуклым, если оно вместе с любыми двумя точками содержит их произвольную выпуклую, линейную комбинацию.

Определение: Угловыми или крайними точками выпуклого множества называются точки, которые не являются выпуклой, линейной комбинацией двух произвольных точек этого же множества.

Определение: Точка множества называется граничной, если любой шар с центром в этой точке содержит как точки принадлежащие множеству, так и точке не принадлежащие ему.

Определение: Граничные точки образуют границу данного множества.

Определение: Замкнутым называют множество, содержащее все свои граничные точки.

Определение: Выпуклым многоугольником называется выпуклое, замкнутое, ограниченное множество на плоскости, имеющее конечное число угловых точек.

Теорема: Замкнутый ограниченный выпуклый многоугольник является выпуклой линейной комбинацией своих угловых точек.

Теорема: Пересечение любого числа выпуклых множеств есть множество выпуклое (если только оно непустое).

Геометрическая интерпретация множества

решений системы линейных неравенств с 2 неизвестными

В общем виде линейное неравенство с 2 переменными записывается следующим образом (1) или (2).

Теорема: Множество решений линейного неравенства (1) служит одна из двух полуплоскостей, на которые всю плоскость делит прямая включая и эту прямую, а другая полуплоскость вместе с этой же прямой является множеством решений линейного неравенства (2).

Возьмем систему из двух неравенств

Множество её решений это точки принадлежащие обеим полуплоскостям. По теореме 2 их пересечения выпуклое множество, имеющая конечное число угловых точек. Методом математический индукции установлено, что множеством решений системы m – линейных неравен ств с дв умя переменными является выпуклый многоугольник (если это пересечение пусто).

Источник