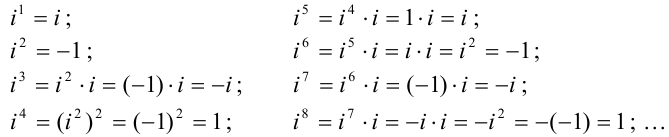Что называется мнимой единицей как вычисляются степени мнимой единицы
Лекция по высшей математике «Мнимая единица. Алгебраическая форма комплексного числа»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Алгебраическая форма комплексного числа.
Цели: расширить понятие числа, ввести понятие мнимой единицы и ее степеней, понятие комплексного числа; рассмотреть алгебраическую форму комплексного числа ; развивать умения обобщать полученные знания, способствовать развитию логического мышления;
воспитывать у обучающихся сознательное отношение к процессу обучения.
Мнимые числа. Определение мнимой единицы. Степени мнимой единицы.
Определение комплексного числа.
Алгебраическая форма комплексного числа.
Например: 
Например: 
и 
и 
.
Теорема. Люб ая натуральн ая степень числа і может быть преобразован а к
Пусть m =4 k +3, тогда і м 
Пример. Вычислить значение выражения 
.
Замечание. Для того, чтобы вычислить степень мнимой единицы, удобно пользоваться таким правилом:
1) разделить показатель степени на 4;
Символически действительную и мнимую части комплексного числа обозначают так: 
(ре зет), 
(им зет).
Замечание. Иногда мнимой частью комплексного числа z = а + b і называют bi.
Для комплексных чисел не существует понятий больше и меньше, то есть комплексные числа не сравнимы.
Определение. Комплексное число (-а- bi ) называется противоположным комплексному числу
Определение. Два комплексных числа, у которых действительные части равны, а мнимые
части противоположные, называются комплексно сопряженными числами и
обозначаются соответственно 
и 
.
3.Алгебраическая форма комплексного числа. Действия над комплексными числами, заданными в алгебраической форме.
Сложение комплексных чисел
Определение. Суммой двух комплексных чисел 
и 
называется
комплексное число 
.
Итак, 
(1)
Таким образом, чтобы сложить два комплексных числа нужно сложить их действительные части, и это дает действительную часть суммы, и сложить мнимые части, что дает мнимую часть суммы.
Сумма сопряженных чисел всегда является действительн ым числом 
то есть, 
. (2)
Вычитание комплексных чисел
Определение. Разностью двух комплексных чисел и называется такое
комплексное число 
, которое в сумме с числом 
дает число 
.
Вычитание комплексных чисел всегда возможно.
Теорема. Для любых комплексных чисел и всегда существует разница 
, которая определена однозначно.
Таким образом, для того, чтобы вычесть комплексные числа, достаточно вычесть их действительные части и их разницу взять за действительную часть разности, а также вычесть мнимую часть разности
Получается, 
(3)
Разность двух сопряженных чисел всегда является мнимым числом. 
,
то есть, 
(4)
Умножение комплексных чисел
Определение. Произведением двух комплексных чисел и называется такое комплексное число, которое определяется формулой: 
(5)
В процессе умножения комплексных чисел лучше выполнять непосредственное умножение. Произведение сопряженных чисел всегда является действительным числом 
. 
Пример. Найти значение выражения 
.
Решение: 
.
Деление комплексных чисел
Определение. Частным двух комплексных чисел и называется такое
комплексное число z, которое в произведении с дает .
Всегда существует частное от деления двух комплексных чисел, если знаменатель отличается от нуля.
Теорема. Частное 
определено и к тому же однозначно для всех комплексных чисел 
и 
, если только 
, то есть 
.
(7)
Пример. Вычислить значение выражения 
.
Решение: 
Над комплексными числами в алгебраической форме возможно выполнять и такие действия, как возведение в степень, извлечения корня. Но выполнение этих действий в алгебраической форме довольно трудоемкое.
Закрепление изученного материала.
1. Вычислить: 
2. Среди приведенных примеров укажите :
а) чисто мнимые комплексные числа;
б) чисто действительные комплексные числа;
в) сопряженные комплексные числа;
г) равные комплексные числа:
3. Выполнить действия: 
Ответ. 
4. На основании равенства комплексных чисел найти действительные числа 
и 
если 
Ответ. 
5. Решить квадратные уравнения и проверить выполнение теоремы Виета:
а) 
б) 
Ответ. а) 
б) 
1.Дать определение комплексного числа.
2.Сформулировать определение мнимой единицы.
3.Как найти степень мнимой единицы.
4.Какие комплексные числа называют равными, сопряженными?
5.Записать формулу для нахождения произвольного степени мнимой единицы.
6. Приведите примеры чисто мнимых чисел.
7. Дать определение суммы, произведения и частного двух комплексных чисел.
Письменный, Д. Т. Конспект лекций по высшей математике: полный курс Д. Т. Письменный. – 9-е изд. – М.: Айрис-пресс, 2009. 608 с.: ил. – (Высшее образование).
Лунгу, К. Н. Сборник задач по высшей математике. 1 курс / К. Н. Лунгу, Д. Т. Письменный, С. Н. Федин, Ю. А. Шевченко. – 7-е изд. – М.: Айрис-пресс, 2008. 576 с.: – (Высшее образование).
Григорьев В. П. Элементы высшей математики: учебник для студ. учреждений сред. проф. образования / В. П. Григорьев, Ю. А. Дубинский. – 10-е изд., стер. – М. Издательский центр «Академия», 2014. – 320 с.
Понятие мнимой единицы
Введение мнимой единицы позволяет нам теперь извлекать квадратные корни даже из отрицательных чисел. Например,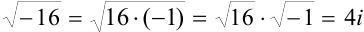 
.
Рассмотрим степени мнимой единицы:
Легко заметить, что значения степеней числа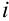 
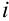
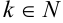
повторяются с периодом, равным четырем. Тогда для нахождения любой натуральной степени числа можно использовать следующие формулы (
):
Пример №42.1.
Вычислить: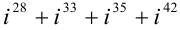 
.
Решение:
Рассмотрим каждое слагаемое в отдельности.
(если показатель степени числа разделился на 4 без остатка, т.е. 
, то применяем формулу 
);
(по формуле 
, в нашем случае 
);
(по формуле 
, в нашем случае );
(по формуле 
, в нашем случае 
).
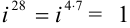
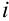
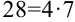
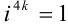
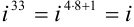
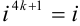
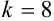
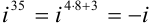
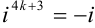
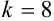
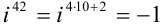
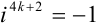
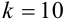
Тогда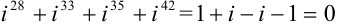 
.
Ответ: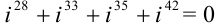 
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №38. Определение комплексного числа. Действия с комплексными числами.
Перечень вопросов, рассматриваемых в теме
1) понятие мнимой единицы;
2) определение комплексного числа;
3) действия с комплексными числами и действия над ними.
Запись комплексного числа в виде a + bi называют алгебраической формой комплексного числа, где а – действительная часть, bi – мнимая часть, причем b – действительное число.
Два комплексных числа z = a + bi и 
= a – bi, отличающиеся лишь знаком мнимой части, называются сопряженными.
Определение. Вычесть из комплексного числа z1 комплексное число z2, значит найти такое комплексное число z,
Теорема. Разность комплексных чисел существует и притом единственная.
Определение. Произведением комплексных чисел z1=a1+ b1 i и z2=a2+b2 i называется комплексное число z, определяемое равенством:
Определение. Разделить комплексное число z1 на комплексное число z2, значит найти такое комплексное число z, что z · z2 = z1.
Теорема. Частное комплексных чисел существует и единственно, если z2 ≠ 0 + 0i.
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Исходя из этого, получим следующее определение комплексного числа.
б) Сложение комплексных чисел определяется правилом:
в) Умножение комплексных чисел определяется правилом:
Запись комплексного числа в виде a + bi называют алгебраической формой комплексного числа, где а – действительная часть, bi – мнимая часть, причем b – действительное число.
Комплексное число a + bi считается равным нулю, если его действительная и мнимая части равны нулю: a = b = 0
Комплексное число a + bi при b = 0 считается совпадающим с действительным числом a: a + 0i = a.
Комплексное число a + bi при a = 0 называется чисто мнимым и обозначается bi: 0 + bi = bi.
Два комплексных числа z = a + bi и 
= a – bi, отличающиеся лишь знаком мнимой части, называются сопряженными.
Над комплексными числами в алгебраической форме можно выполнять следующие действия.
Сложение комплексных чисел обладает следующими свойствами:
3º. Комплексное число – a – bi называется противоположным комплексному числу z = a + bi. Комплексное число, противоположное комплексному числу z, обозначается -z. Сумма комплексных чисел z и -z равна нулю: z + (-z) = 0
Пример 1. Выполните сложение (3 – i) + (-1 + 2i).
(3 – i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.
Определение. Вычесть из комплексного числа z1 комплексное число z2, значит найти такое комплексное число z, что z + z2 =z1.
Теорема. Разность комплексных чисел существует и притом единственная.
Определение. Произведением комплексных чисел z1=a1+ b1 i и z2=a2+b2i называется комплексное число z, определяемое равенством:
Умножение комплексных чисел обладает следующими свойствами:
3º. Дистрибутивность умножения относительно сложения:
На практике умножение комплексных чисел производят по правилу умножения суммы на сумму и выделения действительной и мнимой части.
В следующем примере рассмотрим умножение комплексных чисел двумя способами: по правилу и умножением суммы на сумму.
Пример 3. Выполните умножение (2 + 3i) (5 – 7i).
1 способ. (2 + 3i) (5 – 7i) = (2⋅ 5 – 3⋅ (- 7)) + (2⋅ (- 7) + 3⋅ 5)i =
= (10 + 21) + (- 14 + 15)i = 31 + i.
2 способ. (2 + 3i) (5 – 7i) = 2⋅ 5 + 2⋅ (- 7i) + 3i⋅ 5 + 3i⋅ (- 7i) =
= 10 – 14i + 15i + 21 = 31 + i.
Определение. Разделить комплексное число z1 на комплексное число z2, значит найти такое комплексное число z, что z · z2 = z1.
Теорема. Частное комплексных чисел существует и единственно, если z2 ≠ 0 + 0i.
На практике частное комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю.
Пусть z1 = a1 + b1i, z2 = a2 + b2i, тогда 
В следующем примере выполним деление по формуле и правилу умножения на число, сопряженное знаменателю.
Пример 4. Найти частное
5) Возведение в целую положительную степень.
а) Степени мнимой единицы.
i 8 = i 6 i 2 = 1 и т. д.
Поэтому, чтобы возвести число i в целую положительную степень, надо показатель степени разделить на 4 и возвести i в степень, показатель которой равен остатку от деления.
i 36 = (i 4 ) 9 = 1 9 = 1,
i 17 = i 4⋅ 4+1 = (i 4 ) 4 ⋅ i = 1 · i = i.
б) Возведение комплексного числа в целую положительную степень производится по правилу возведения двучлена в соответствующую степень, так как оно представляет собой частный случай умножения одинаковых комплексных сомножителей.
Пример 6. Вычислите: (4 + 2i) 3
(4 + 2i) 3 = 4 3 + 3⋅ 4 2 ⋅ 2i + 3⋅ 4⋅ (2i) 2 + (2i) 3 = 64 + 96i – 48 – 8i = 16 + 88i.
Стоит отметить. что с помощью комплексных чисел можно решать квадратные уравнения, у которых отрицательный дискриминант.
Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен.
Пример 7. Решите уравнения:
а) x 2 – 6x + 13 = 0; б) 9x 2 + 12x + 29 = 0.
Решение. а) Найдем дискриминант по формуле
D = b 2 – 4ac.
Так как a = 1, b = – 6, c = 13, то
D = (– 6) 2 – 4×1×13 = 36 – 52 = – 16;
Корни уравнения находим по формулам
б) Здесь a = 9, b = 12, c = 29. Следовательно,
D = b 2 – 4ac =122 – 4×9×29 = 144 – 1044 = – 900,
Находим корни уравнения:
Мы видим, что если дискриминант квадратного уравнения отрицателен, то квадратное уравнение имеет два сопряженных комплексных корня.
Разбор решения заданий тренировочного модуля
№1. Тип задания: единичный выбор
Вычислите сумму (2 + 3i)+ (5 – 7i).
Можем сделать вывод, что верный ответ
№2. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.