Что называется логической величиной
Урок 20
Условия поиска информации,
простые логические выражения
Основы логики:
логические величины и формулы
Изучаемые вопросы:
— Понятие логического выражения.
— Операции отношения.
— Запросы на выборку с использованием простых логических выражений.
Основные темы:
— формальная логика и алгебра логики;
— логические величины, операции, формулы;
— таблица истинности.
Содержание урока
Логические операции
Логические операции
Логические величины
Алгебра логики оперирует с логическими величинами, которые принимают всего два значения: «истина» или «ложь». Следовательно, каждая такая величина может быть сопоставлена некоторому высказыванию, иднако алгебра логики — это формализованная математическая дисциплина, поэтому логическая величина не должна обязательно иметь конкретный содержательный смысл.
Как принято в алгебре чисел, в алгебре логики логические величины могут быть константами и переменными. Логические константы обозначаются либо словами ИСТИНА и ЛОЖЬ, либо по-английски TRUE, FALSE. Логические переменные обозначаются символическими (буквенными) именами: X, A, Z, D2 и т. п. Алгебра чисел работает на числовом множестве значений величин, которыми она оперирует. Множество чисел бесконечно. Алгебра логики работает на множестве, состоящем всего из двух значений: «истина» и «ложь». В этом смысле она проще алгебры чисел.
Логические операции
В алгебре логики имеются шесть логических операций. Они называются так:
1) отрицание (инверсия);
2) логическое умножение (конъюнкция);
3) логическое сложение (дизъюнкция);
4) разделительная дизъюнкция;
5) следование (импликация);
6) эквивалентность.
Первые три являются основными логическими операциями. Три последние могут быть выражены через основные операции. Поэтому в дальнейшем мы будем рассматривать только три операции: отрицание, логическое умножение и логическое сложение.
Правила выполнения логических операций нетрудно запомнить.


Результатом логического умножения будет ИСТИНА, только если истинны значения обоих операндов: истина и истина = истина. Во всех остальных случаях результатом будет ЛОЖЬ. Для обозначения операции логического умножения используют связку «и».
Результат логического сложения — ЛОЖЬ только в том случае, если оба операнда имеют значение ЛОЖЬ: ложь или ложь = ложь. Во всех остальных случаях будет ИСТИНА. Для обозначения операции логического сложения используют связку «или».
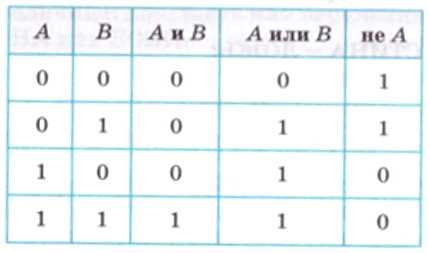
Таблица на рис. 3.1 иллюстрирует вед» правила выполнения трех логических операций. Такую таблицу называют таблицей истинности. В ней буквами А и Б обозначены логические операнды. Величина ИСТИНА обозначена цифрой 1, логическая величина ЛОЖЬ цифрой 0.
Рис. 3.1. Таблица истинности
Следующая страница 
§ 18. Логические величины, операции, выражения
С элементами математической логики вы уже встречались в курсе информатики основной школы, изучая способы записи запросов к базе данных и условной функции ЕСЛИ в электронных таблицах, основы алгоритмизации и программирования. Повторим основные понятия логики с целью дальнейшего углубления ваших знаний в использовании ее для программирования.
К числу основных понятий логики относятся: высказывание, логическая величина, логические операции, логические выражения и формулы.
Высказывание (суждение) — это повествовательное предложение, в котором что-либо утверждается или отрицается. По поводу любого высказывания можно сказать, истинно оно или ложно.
Например, высказывание «На улице идет дождь» будет истинным или ложным в зависимости от состояния погоды в данный момент. Истинность высказывания «Значение А больше, чем Б», записанного в форме неравенства: А > В, будет зависеть от значений переменных А и В.
Логические величины — понятия, выражаемые словами: ИСТИНА, ЛОЖЬ (true, false). Следовательно, истинность высказываний выражается через логические величины.
Логическая константа: ИСТИНА или ЛОЖЬ.
Логическая переменная: символически обозначенная логическая величина. Следовательно, если известно, что А, В, X, Y и др. — переменные логические величины, то, значит, они могут принимать значения только ИСТИНА или ЛОЖЬ.
Логическое выражение — простое или сложное высказывание. Сложное высказывание строится из простых с помощью логических операций (связок).
Логические операции
Конъюнкция (логическое умножение). В русском языке она выражается союзом И. В математической логике используются знаки & или ∧. Конъюнкция — двухместная операция; записывается в виде: А & В. Значением такого выражения будет ЛОЖЬ, если значение хотя бы одного из операндов ложно.
Дизъюнкция (логическое сложение). В русском языке этой связке соответствует союз ИЛИ. В математической логике она обозначается знаком ∨. Дизъюнкция — двухместная операция; записывается в виде: A ∨ В. Значением такого выражения будет ИСТИНА, если значение хотя бы одного из операндов истинно.
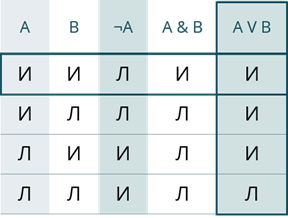
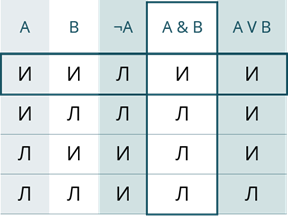
Правила выполнения рассмотренных логических операций отражены в следующей таблице, которая называется таблицей истинности логических операций (здесь И означает «истина», Л — «ложь»):
Логическая формула — формула, содержащая лишь логические величины и знаки логических операций. Результатом вычисления логической формулы является ИСТИНА или ЛОЖЬ.
Последовательность выполнения операций в логических формулах определяется старшинством операций. В порядке убывания старшинства логические операции расположены так: отрицание, конъюнкция, дизъюнкция. Кроме того, на порядок выполнения операций влияют скобки, которые можно использовать в логических формулах.
Например:
Пример. Вычислить значение логической формулы:
если логические переменные имеют следующие значения: X = ЛОЖЬ, У = ИСТИНА, Z = ИСТИНА.
Решение. Отметим цифрами сверху порядок выполнения операций в формуле:
Логические функции на области числовых значений
Алгебра чисел пересекается с алгеброй логики в тех случаях, когда приходится проверять принадлежность значений алгебраических выражений некоторому множеству. Например, принадлежность значения числовой переменной X множеству положительных чисел выражается через высказывание: «X больше нуля». Символически это записывается так: Х > 0. В алгебре такое выражение называют неравенством. В логике — отношением.
Отношение X > О может быть истинным или ложным. Если X — положительная величина, то оно истинно, если отрицательная, то ложно. В общем виде отношение имеет следующую структуру:
Здесь выражения 1 и 2 — некоторые математические выражения, принимающие числовые значения. В частном случае выражение может представлять собой одну константу или одну переменную величину. Знаки отношений могут быть следующими:
0 — всегда ИСТИНА, 3 ≠ 6 : 2 — всегда ЛОЖЬ; так и переменной: а 0) или Р(х, у) = (х 2 2 + У 2 2 и Rl 2 2 + У 2 2 и R2 2 — правая граница, парабола.
Рассматриваемая область есть пересечение трех полуплоскостей, описываемых неравенствами:
Во внутренних точках все эти три отношения являются одновременно истинными. Поэтому искомый предикат имеет вид:
Логические выражения на Паскале
Уже говорилось о том, что в Паскале имеется логический тип данных.
Логические константы: true (истина), false (ложь).
Логические переменные: описываются с типом Boolean.
Операции отношения: осуществляют сравнение двух операндов и определяют, истинно или ложно соответствующее отношение между ними. Знаки операций отношения: = (равно), <> (не равно), > (больше), = (больше или равно),
Вопросы и задания
а) все числа X, Y, Z равны между собой;
б) из чисел X, У, Z только два равны между собой;
в) каждое из чисел X, У, Z положительно;
г) только одно из чисел X, У, Z положительно;
Пояснения: odd(x) — логическая функция определения четности аргумента, равна true, если х — нечетное, и равна false, если х — четное; trunc (х) — целочисленная функция от вещественного аргумента, возвращающая ближайшее целое число, не превышающее х по модулю.
Презентация на тему Логические величины, операции, выражения
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Описание слайда:
Логические величины, операции, выражения
ГБОУ СПО «НТСТиСО»
Баландина Татьяна Александровна
Преподаватель информатики
Описание слайда:
Описание слайда:
Логические выражения и логические операции
Описание слайда:
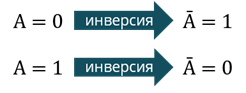
Логическое отрицание (инверсия)
Описание слайда:
Описание слайда:
Логическое сложение (дизъюнкция)
Если два высказывания соединены союзом «ИЛИ», то полученное сложное высказывание обычно считается истинным, когда истинно, хотя бы одно из составляющих высказываний. Дизъюнкцией называется такое новое высказывание, которое истинно тогда и только тогда, когда истинно хотя бы одно из этих высказываний.
Дизъюнкцию высказываний А и В мы обозначим символом А V В и будем читать: А или В. Определение дизъюнкции может быть записано в виде таблицы истинности:
Описание слайда:
Логическое следование (импликация)
Импликацией называется высказывание, которое ложно тогда и только тогда, когда А истинно и В ложно.
Запишем это определение в виде таблицы истинности:
Описание слайда:
Логическое тождество (эквиваленция)
Эквиваленцией двух высказываний А и В называется такое высказывание, которое истинно тогда и только тогда, когда оба эти высказывания А и В истинны или оба ложны.
Отметим, что высказывание типа «А, если и только если В» можно заменить высказыванием «Если А, то В и, если В, то А» (обдумайте это на досуге и обратите внимание на символ ). Следовательно, функцию эквиваленции можно заменить комбинацией функций импликации и конъюнкции. Запишем таблицу истинности для эквиваленции:
Описание слайда:
Построение таблиц истинности для логических функций
Описание слайда:
Логические функции и их преобразования. Законы логики
Для операций конъюнкции, дизъюнкции и инверсии определены законы булевой алгебры, позволяющие производить тождественные (равносильные) преобразования логических выражений.
Законы логики
1. закон двойного отрицания;
2. A&B = B&A коммутативность конъюнкции;
3. AVB = BVA коммутативность дизъюнкции;
4. A&(B&C) = (A&B)&C ассоциативность конъюнкции;
5. AV(BVC) = (AVB)VC ассоциативность дизъюнкции;
6. A&(BVC) = (A&B)V(A&C) дистрибутивность конъюнкции относительно дизъюнкции;
7. AV(B&C) = (AVB)&(AVC) дистрибутивность дизъюнкции относительно конъюнкции;
8. A&A = A
9. AVA = A
10. A Ú (A&B) = A; A&(A Ú B) = A законы поглощения
11. (A&B) Ú ( &B) = B; (A Ú B)&( Ú B) = B законы исключения (склеивания)
12. (A Û B) = (BÛ A) закон контрапозиции (правило перевертывания)
Описание слайда:
Вопросы для самоконтроля
Основные логические операции: конъюнкция, дизъюнкция (оба вида), отрицание, импликация, эквивалентность. Примеры логических выражений.
Таблица истинности. Примеры. A and not A; A or not A
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Логические величины, операции и выражения
Урок 21. Информатика 10 класс (ФГОС)
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Логические величины, операции и выражения»
На этом уроке мы с вами вспомним, что такое логические величины, проанализируем такие логические операции, как конъюнкция, дизъюнкция и инверсия. Также поработаем с логическими выражениями.
В курсе информатики вы уже проходили логические величины, выражения и операции. Давайте вспомним, что такое высказывание. Высказывание – это повествовательное предложение на любом языке, в котором что-либо утверждается или отрицается. То есть любое высказывание можно определить, как истинное или ложное.
Рассмотрим следующие предложения:
· Клавиатура предназначена для ввода текстовой информации и команд управления компьютером.
· При приёме информации происходит процесс переноса информации от источника к приёмнику.
Эти предложения будут относится к высказываниям, так как можно точно сказать истины они или ложны. Первое высказывание является истинным, а второе – ложным.
А вот следующие предложения:
· Не поднимай телефон!
Не являются высказываниями, так как в определении сказано, что высказывание – это повествовательно предложение.
Для построения высказываний могут использоваться знаки различных формальных языков: математики, физики, химии и других.
Числовые выражения не являются высказываниями. Но, в то же время, если из двух выражений составить одно и соединить их знаком равенства или неравенства, то новое выражение будет высказыванием.
Логические высказывания бывают простыми и составными.
Простое высказывание – это высказывание, в котором никакая его часть сама не является высказыванием.
Сложное или же составное высказывание – это высказывание, которое строится из простых с помощью логических операций.
Логические величины – это понятия, выражаемые словами Истина (True), Ложь (False). Истинность высказывания выражается через логические величины.
Логическая переменная – это символически обозначенная логическая величина. То есть логическая величина может обозначаться, например, буквой латинского алфавита. Сама же буква будет являться переменной логической величины. В свою очередь, она может принимать только значение Истина или Ложь.
Логическое выражение – это простое или сложное высказывание. Сложное высказывание, как мы уже знаем, строиться из простых при помощи логических операций (связок).
К логическим операциям относятся конъюнкция, дизъюнкция и инверсия (отрицание). Давайте рассмотрим каждую логическую операцию.
Итак, первая логическая операция – конъюнкция – логическое умножение.
Конъюнкция – это логическая операция, которая объединяет два высказывания в одно новое, которое будет являться ложным тогда, когда хотя бы одно из исходных высказываний ложно. Конъюнкция – это двухместная операция, то есть в ней должны присутствовать две логические переменные.
В естественном языке конъюнкция соответствует союзу «И». В алгебре конъюнкция может обозначаться с помощью нескольких знаков: знака амперсанда «&», знака конъюнкции «/\», а также знака умножения «·». В языках программирования для обозначения конъюнкции используется английский союз «AND», знак амперсанда «&» или же двойной знак амперсанда «&&».
Следующая операция – дизъюнкция. Ещё её называют логическим сложением.
Дизъюнкция – это логическая операция, которая объединяет два высказывания в одно новое, которое будет истинным тогда, когда хотя бы одно исходное высказывание истинно. Дизъюнкция также является двухместной операцией, то есть в ней должны присутствовать две логические переменные.
В различных сферах применения, дизъюнкция обозначается по-разному. В естественном языке это союз «ИЛИ». В алгебре высказываний используется следующий знак: «V». Или знак «+». В программировании в основном используется английское «OR». Но в некоторых языках программирования дизъюнкция обозначается следующими знаками: «|», «||».
И последняя логическая операция – инверсия – отрицание.
Отрицание – это логическая операция, которая преобразует исходное высказывание в новое, значение которого противоположно исходному. А вот отрицание является унарной (одноместной) операцией.
Давайте посмотрим, как обозначается инверсия в различных сферах её применения. В естественном языке инверсии соответствуют речевой оборот «неверно, что» и частица «не». В алгебре высказывания инверсия обозначается следующими знаками: «¬», «ˉ». А вот в сфере программирования используется английское слово «NOT».
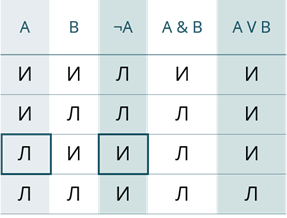
Давайте составим таблицу истинности для всех логических операций. В ней И – это истина, Л – Ложь.
В первых двух столбцах предоставлены всевозможные исходные данные А и B.
В третьем столбце будет идти ¬А.
Как мы с вами знаем из определения операция отрицания преобразует исходное выражение в новое, значение которого противоположно исходному. То есть, если А было истинно, при отрицании оно станет ложным. И наоборот, если выражение было ложным, то оно станет истинным. Заполним третий столбец таблицы исходя из данных первого.
Далее идёт конъюнкция. Здесь мы будем смотреть на значения, которые принимают выражения А и B. Мы с вами знаем, что при конъюнкции новое высказывание будет являться ложным тогда, когда хотя бы одно из исходных высказываний ложно. То есть, исходя из данных нашей таблицы, в первой строке оба высказывания истины, значит и новое будет истинно. А вот все остальные будут ложными, так как во второй строке ложно высказывание B, в третьей – А, а в четвёртой – оба.
И последний, пятый столбец – дизъюнкция. Снова будем брать значения выражений А и B. Новое высказывание будет истинным тогда, когда хотя бы одно исходное высказывание истинно. Значит в первых трёх строках 5 столбца новые выражения будут истинны, так как в первой строке истинны оба высказывания А и B, во второй – А, в третьей – B. А вот в четвёртой строке мы можем видеть, что значения А и B оба ложны, значит и новое выражение будет ложно.
Логическая формула – это формула, которая содержит только логические величины и знаки логических операций. Результатом вычисления такой формулы будет являться истина или ложь.
При выполнении операций в формуле нужно придерживаться следующего порядка:
Но также стоит помнить, что операции в скобках выполняются в первую очередь. Если же у нас идут несколько равнозначных операций подряд, то выполнение их будет происходить слева направо.
Давайте разберёмся на примере. Вычислить значение логической формулы, если логические переменные имеют следующие значения: А – Истина, B – истина, C – Ложь.
Перейдём к решению. Для начала проставим над каждой операцией номер порядка, в котором она будет исполняться.
В первую очередь будут выполняться операции в скобках. А первой будет ¬C.
Затем дизъюнкция: B V ¬C.
После этого будем выполнять конъюнкцию: A & (B V ¬C).
А затем оставшуюся дизъюнкцию: A & (B V ¬C) V B.
Давайте запишем наши вычисления пошагово:
Первое действие – отрицание. Переменная С имеет значение Ложь. Смотрим на таблицу истинности и видим, что при отрицании мы получим значение Истина.
Вторым действием выполняется дизъюнкция. B = Истине, ¬C = Истине. При дизъюнкции двух истин мы получим истину.
Третье действие. Конъюнкция. А = Истине, B V ¬C = Истине. При конъюнкции двух истин мы получим истину.
И четвёртое действие – дизъюнкция. При дизъюнкции двух истин снова получим истину.
Таким образом значение логической формулы равно истине.
A & (B V ¬C) V B = ИСТИНА
А сейчас рассмотрим логические функции на области числовых значений. Изучением числовых значение занимается алгебра чисел, а логических функций – алгебра логики. Две этих науки могут пересекаться в том случае, если необходимо проверить принадлежность значений алгебраических выражений некоторому множеству. Если нам нужно, например, проверить принадлежность значения числовой переменной А к множеству отрицательных чисел, то это можно выразить через высказывание: «А меньше нуля». В алгебре это можно записать следующим образом: A
Если в отношение входят переменные числовые величины, то и значение отношения будет логической переменной.
Идём дальше. Отношение также можно рассматривать как логическую функцию от числовых аргументов. Например, F (x) = x –2;