Что называется линейной скоростью материальной точки в каких единицах она измеряется
Линейная скорость
Для характеристики вращательного движения, кроме угловой скорости, вводится понятие линейной скорости.
Линейной скоростью называется скорость, с которой точка движется по окружности.
Формулу для величины линейной скорости можно вывести на основании следующих рассуждений.
Точка, лежащая на окружности радиуса R, за один оборот пройдёт путь, равный длине окружности 2πR, за время, равное периоду Т. Взяв отношение пути 2πR ко времени T, мы получим скорость движения точки по окружности:
v = 2 πR /T
Но 1 /Т = n; следовательно,
v = 2πRn
Связь между угловой и линейной скоростями
Отсюда легко установить связь между линейной и угловой скоростями. Мы уже знаем, что угловая скорость связана с числом оборотов формулой: ω = 2πn; поэтому на основании формулы скорости движения по окружности получим:
v = ωR
Линейная скорость точки, движущейся равномерно по окружности, равна угловой скорости, умноженной на радиус окружности.
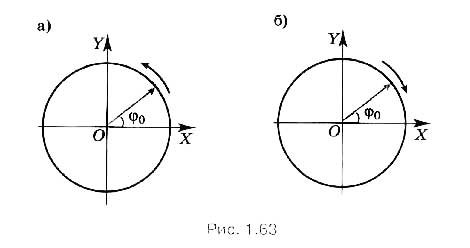
Известно, что вектор скорости точки, движущейся по окружности, направлен по касательной. Следовательно, линейная скорость направлена по касательной к окружности.
Разрешено частичное копирование статей с обязательной ссылкой на источник
Связь между угловой и линейной скоростями
Отсюда легко установить связь между линейной и угловой скоростями. Мы уже знаем, что угловая скорость связана с числом оборотов формулой: ω = 2πn; поэтому на основании формулы скорости движения по окружности получим:
Линейная скорость точки, движущейся равномерно по окружности, равна угловой скорости, умноженной на радиус окружности.
Известно, что вектор скорости точки, движущейся по окружности, направлен по касательной. Следовательно, линейная скорость направлена по касательной к окружности.
14. Что называется линейным ускорением материальной точки, в каких единицах оно измеряется?
Формула линейного ускорения:
15. Закон равноускоренного движения по прямой
равноускоренным движением называют такое движение, при котором вектор ускорения остается неизменным по модулю и направлению.
Закон равноускоренного движения по прямой
Это выражение называют законом равноускоренного движения
16. Что называется угловой скоростью, в каких единицах оно измеряется?
Угловая скорость — величина, характеризующая скорость вращения материальной точки вокруг центра вращения.
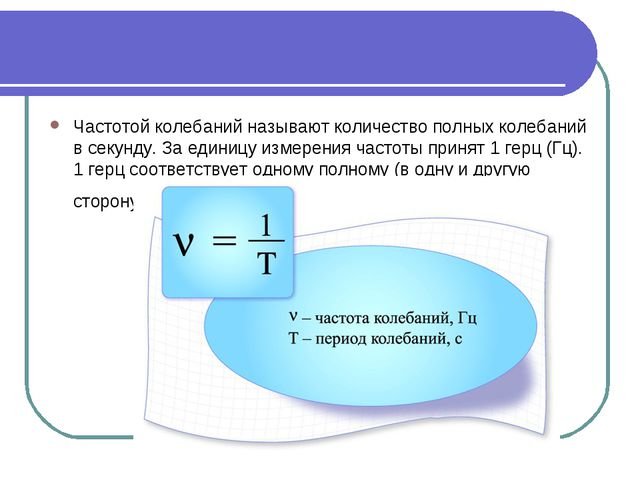
17. Что называется частотой вращения, в каких единицах оно измеряется?
Частота вращения — это физическая величина, равная числу полных оборотов за единицу времени
18. Что называется периодом вращения, в каких единицах он измеряется?
Период вращения (физический термин) — промежуток времени, в течение которого точка совершает полный оборот, двигаясь по окружности.
19. Связь между угловой скоростью вращения и его частотой.
Угловая скорость вращения ω это отношение угла, на которое тело повернется, к времени, за которое оно это сделает. Полному обороту вокруг оси соответствует угол 2π или 360° в зависимости от единиц измерения угла. Число оборотов равно отношению пройденного угла к 2π или 360°. Частота вращения это число полных оборотов тела вокруг оси за единицу времени, таким образом она равна ω/(2π) или ω/360° для углов, измеряемых в градусах
20. Связь между угловой скоростью и периодом.
21. Связь между линейной и угловой скоростями
Связь между линейной и угловой скоростью. Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть ее отличие от угловой скорости. При вращении твердого тела разные его точки имеют разные линейные скорости, но угловая скорость для всех точек одинакова. Междулинейной скоростью какой-либо точки вращающегося тела и угловой скоростьсуществует связь. Точка, лежащая на окружности радиуса R, за один оборот пройдет путь 2πR. А так как, время одного оборота тела есть период Т, то модуль линейнойскорости можно найти так: v=2πR/T=2πRν или v=ωR
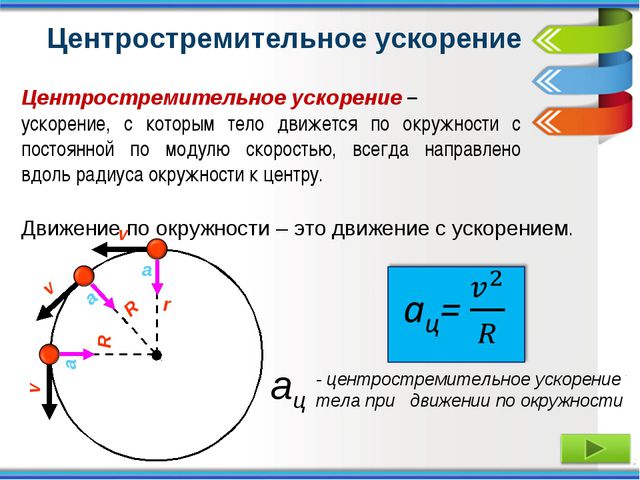
22. Центростремительное ускорение
»
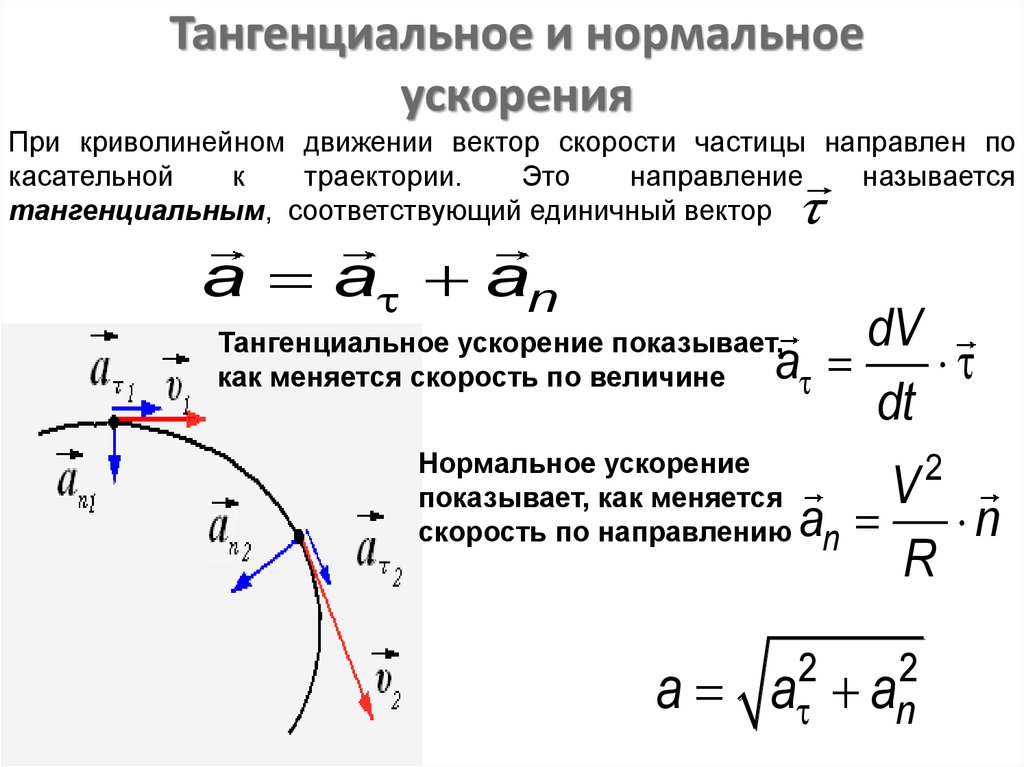
23. Что называется нормальным ускорением материальной точки, как его вычислить?
24. Что называется тангенциальным ускорением материальной точки, как его вычислить?
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
25. Напишите формулу для определения полного ускорения материальной точки
26. Какое падение тела называется свободным?
Свободным падением называется движение, которое совершило бы тело только под действием силы тяжести без учета сопротивления воздуха.
Линейная и угловая скорость
Линейная скорость
Векторная величина равная:
называется мгновенной скоростью или просто скоростью.
Скорость прохождения пути определена аналогично:
Из формулы (5) следует, что проекции скорости на оси координат X, Y,Z равны:
При этом модуль скорости найдем в соответствии с выражением:
Единицей скорости является скорость такого движения, при котором перемещение точки в единицу времени равно единице длины:
В Международной системе единиц (СИ) единицей измерения линейной скорости (в том числе и средней скорости) является метр в секунду:
Угловая скорость
Угловой скоростью называют векторную величину, равную первой производной от угла поворота по времени:
Связь между линейной и угловой скоростями задана выражением:
В векторном виде формулу (8) записывают как:
При равномерном движении по окружности угловая скорость ($\omega =const$), частота и период связаны как:
\[\omega =\frac<2\pi >
Примеры задач на линейную и угловую скорость
Решение: Основой для решения задачи будет определение величины угловой скорости:
\[\omega =\frac
Задание: Материальная точка движется в плоскости XOY. Ее движение описывают уравнения:
$(A,B-постоянные,\ больше\ нуля)$. Запишите закон изменения скорости движения точки ($\overline
Решение: Закон движения точки задан в координатной форме. В векторном виде его запишем как:
Скорость движения найдем в соответствии с ее определением:
Величину скорости найдем, зная из уравнения (2.2), что:
модуль скорости равен:
Формула для расчета линейной скорости
Вы будете перенаправлены на Автор24
Понятие скорости
Также скорость часто измеряют в км/ч, км/с, см/с.
Рассмотрим простой пример задачи на вычисление скорости.
Задача. Двигаясь равномерно, поезд за 4 ч проходит 219 км. Найти его скорость движения.
Из примера мы видим, что числовое значение скорости отличается в зависимости от выбранной единицы измерения.
Готовые работы на аналогичную тему
В свою очередь, такие величины как путь, время, длина и другие характеризуются только числовым значением. Тогда говорят, что это скалярные физические величины.
Линейная скорость
Определение линейной скорости относится к разделу физики о механике и подразделу о кинематике в рамках вопроса движения по окружности. В измерении скорости движения по окружности выделяют угловую скорость и линейную скорость.
Дадим определение линейной скорости.
Формула линейной скорости:
Также существует иной вариант этой формулы:
Есть ещё одна формула, по которой можно найти линейную скорость:
$2\pi$ соответствует полной окружности (360 угловым градусам).
$\vec V$ направленена по касательной к тракетории.
Связь между линейной и угловой скоростями
Чтобы проследить связь между линейной и угловой скоростями, нужно дать определение угловой скорости.
Записывается эта формула следующим образом:
В системе СИ угловая скорость измеряется в рад/с.
Угловую скорость также называют циклической частотой вращения, потому что при вращении твёрдого тела угловая скорость всех его точек одинакова.
Эта формула выводится из определения модуля центростремительного ускорения.
Таким образом, в данной статье мы разобрали следующие понятия:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 17 04 2021
Формулы для расчета линейной скорости
Что такое линейная скорость, единицы измерения
Скоростью при равномерном движении тела называют физическую величину, с помощью которой определяют путь, преодоленный телом за единицу времени.
В международной системе СИ единицей измерения линейной скорости является производная от двух основных единиц:
В международной системе СИ скорость измеряется в метрах в секунду (м/с). За единицу скорости принимают скорость равномерного движения, при которой путь в один метр тело преодолеет в течение одной секунды. Кроме того, скорость можно измерять в:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Связь между линейной и угловой скоростями
Скорость точки, которая совершает круговое движение, называется линейной скоростью, чтобы отделить это понятие от термина угловая скорость. Во время вращения абсолютно твердое тело в разных точках будет обладать неодинаковыми линейными скоростями, но значение угловой скорости остается стабильным.
Можно установить связь между линейной и угловой скоростью тела, вращающегося по окружности. Путь, который проходит точка, расположенная на окружности с радиусом R, составляет:
Исходя из того, что время одного оборота тела является периодом Т, модуль линейной скорости будет рассчитан по следующей формуле:
получим справедливое равенство:
Данная формула демонстрирует увеличение линейной скорости тела при его удалении от оси вращения. К примеру, точки, которые движутся по земному экватору v=463 м/с, а точки, расположенные на широте города Санкт-Петербург, движутся со скоростью v=233 м/с. При нахождении на полюсах планеты скорость уменьшается до v=0.
Модуль центростремительного ускорения точки тела, которая совершает равномерные вращательные движения, определяют с помощью угловой скорости тела и радиуса окружности. Уравнение будет записано в следующем виде:
Таким образом, формула будет преобразована:
Подытожив расчеты, можно записать все возможные равенства, справедливые для определения центростремительного ускорения:
Таким образом, рассматривают пару простейших движений, характерных для абсолютно твердого тела, включая поступательное и вращательное. При этом стоит отметить, что определить любое сложное движение, которое совершает абсолютно твердое тело, можно с помощью суммы двух независимых движений:
С помощью закона независимости движений описывают сложное движение абсолютно твердого тела.
Формулы для нахождения линейной скорости
Тело движется равномерно тогда, когда его скорость характеризуется постоянной величиной. Формула для расчета скорости такого движения будет иметь следующий вид:
где s является пройденным путем, то есть длиной линии;
t представляет собой время, в течение которого тело преодолевало указанный путь.
Линейной скоростью V называют физическую величину, которая демонстрирует путь, пройденный телом в течение определенного времени.
Основной формулой для определения линейной скорости является следующее равенство:
где S является путем,
t обозначает время, в течение которого тело преодолело путь S.
Иной вариант уравнения имеет такой вид:
где l является путем,
t обозначает время, в течение которого тело преодолело дугу l.
В некоторых научных источниках скорость обозначают с помощью маленькой буквы v. Другим уравнением для расчета линейной скорости является равенство:
В данном случае 2π представляет собой полную окружность и составляет 360 угловых градусов. Вектор скорости направлен по касательной к траектории движении тела.
Модуль скорости
Числовое значение скорости может быть разным в зависимости от выбранной единицы измерения. Кроме числового значения, скорость характеризуется направлением. Числовое значение, которым обладает скорость, в физике называют ее модулем.
В случае, когда скорость обладает определенным направлением, такая величина является векторной. Таким образом, скорость представляет собой векторную физическую величину. Записывают модуль скорости в виде буквы v, а вектор скорости, как \(\vec
Следует отметить, что такие величины, как путь, время, длина обладают только числовым значением. Они называются скалярными. Если тело движется неравномерно, то справедливо использовать в расчетах среднюю скорость.
Задачи с примерами решения
Задача №1
Тело совершает движение по окружности с ускорением 3 м/с в квадрате. Радиус окружности равен 40 метров. Необходимо определить линейную скорость движения тела.
Ускорение в данном случае будет нормальным. Исходя из этого, определить линейную скорость тела можно с помощью формулы:
Ответ: линейная скорость равна 10,9 м/с.
Задача №2
Поезд совершает равномерное движение. В течение 4 часов он преодолевает путь в 219 километров. Требуется рассчитать скорость движения поезда.
Исходя из основной формулы для расчета линейной скорости, получим:
Ответ: скорость движения поезда составит 54.75 км/ч или 15.2 м/с.
Задача №3
Транспортное средство, работая на двигателе внутреннего сгорания, в течение 2,5 часов преодолевает расстояние в 213 километров. Требуется определить скорость движения транспорта.
С помощью уравнения расчета скорости можно записать решение задачи:
Ответ: Скорость движение транспортного средства составляет 85.2 км/ч или 23.7 м/с.