Что называется кинематической цепью механизмом

iSopromat.ru

Рассмотрим понятия кинематической цепи и механизма:

Кинематическая цепь

Кинематическая цепь – это сочетание звеньев, соединенных в кинематические пары. Имеется определенная классификация кинематических цепей – цепи могут быть простыми и сложными, замкнутыми (закрытыми) и разомкнутыми (открытыми), пространственными и плоскими.

Ранее считалось, что механизм может быть сформирован только на основе замкнутой цепи. Однако с развитием робототехники в качестве механизмов стали широко применяться разомкнутые (открытые) цепи. Поэтому данная классификация в некоторой степени утратила свое первоначальное значение.

Механизм

Механизмом называется кинематическая цепь, имеющая стойку (т.е. звено, принятое за неподвижное), в которой движение одного или нескольких звеньев полностью определяет характер движения остальных звеньев этой цепи.

Другими словами, — это кинематическая цепь, обладающая определенностью движения всех звеньев. Только одним звеньям дается принудительное движение (определенным образом задаются их законы движения, например, подсоединением к двигателю), а другие получают движение от этих звеньев. В итоге механизм можно трактовать как механическую систему тел, предназначенную для преобразования, движения одного или нескольких тел в требуемое движение других тел.

Звенья, законы движения которых заданы, называются входными.

Звенья, законы которых надо определить, называются выходными. Количество входных звеньев определяется числом степеней свободы кинематической цепи, положенной в основу данного механизма.

Понятия входное и выходное (вход и выход) – это кинематическая характеристика. Не надо путать с понятиями – ведущее звено и ведомое звено. Ведущим звеном называется звено, к которому подводится мощность;
ведомое звено – звено, с которого снимается мощность (для выполнения полезной работы).

Таким образом, понятия ведущее и ведомое звено – это силовая (энергетическая) характеристика. Однако в подавляющем большинстве случаев входное звено одновременно является и ведущим, выходное звено – ведомым.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Кинематические цепи и их классификация

Определения: машина, механизм, звено механизма, виды звеньев

Машинойназывается искусственные устройства, выполняющие механические движения для преобразования энергии, материалов и информации. Основной признак машин – совершение некоторой полезной работы. Механизмом называют искусственно созданную систему тел, предназначенную для преобразования механического движения одного или нескольких требуемых движений других тел. Звеньями называют твёрдые тела, входящие в состав механизма и обладающие относительной подвижностью. Звенья могут состоять из одной или несколько жёстко связанных между собой частей, называемых деталями.

Классификация звеньев:

Стойка – неподвижное звено механизма (обозначают нулевой позицией)

Кривошип – звено, совершающее вращательное движение вокруг неподвижной оси.

Коромысло – звено, совершающее угловые качательные движения вокруг неподвижной оси.

Ползун – звено, совершающее линейные возвратно-поступательные движения.

Шатун – звено, совершающее плоскопараллельное движение.

Кулиса – звено, являющееся подвижно направляющее для ползуна (шатуна).

Кулачок – звено, кривизна профиля которого определяет закон движения связанного с ним звена, толкателя.

Кинематические пары и их классификация

Кинематической парой называются подвижные соединения двух соприкасающихся звеньев.

Любая кинематическая пара ограничивает взаимное движение звеньев, т.е. исключает одну или несколько степеней свободы.

Классификация кинематических пар:

По характеру относительного движения:

плоские – движение в одной плоскости

пространственные – движения в разных плоскостях

По характеру соприкосновения:

высшие – соприкосновение звеньев происходит по линии или точке (рельс)

низшие – соприкосновение звеньев происходит по поверхности (ползун)

По количеству условий связей, налагаемых кинематической парой на относительное движение звеньев.

Ограничение, налагаемое на движение звеньев, называется связями.

Классом кинематической пары называется число S условий связи, налагаемых кинематической парой на относительное движение звеньев.

S – число условий связи

H – число степеней свободы

Кинематические цепи и их классификация

Кинематическая цепь – связанная система звеньев, образующих между собой кинематические пары.

Классификация кинематических цепей:

Плоские – при закреплении одного звена, остальные звенья совершают плоское движение, параллельно некоторой неподвижной плоскости.

Пространственные – при закрепление одного звена, остальные звенья совершают движение в различных плоскостях.

Простые – в каждое звено входит не более, чем две кинематические пары.

Сложные – хотя бы одно звено имеет более двух кинематических пар.

Замкнутые – входит не более чем две кинематические пары, и эти звенья образуют один или несколько замкнутых контуров

Разомкнутые – звенья не образуют замкнутый контур.

Источник

Кинематическая цепь

Связанная система звеньев, образующих между собой кинематические пары, называется кинематической цепью.

Кинематические цепи по характеру относительного движения звеньев разделяются на плоские и пространственные.

Кинематическая цепь называется тоской, если точки звеньев описывают траектории, лежащие в параллельных плоскостях. Кинематическая цепь называется пространственной, если точки ее звеньев описывают неплоские

траектории или траектории, лежащие в пересекающихся плоскостях. Наи­большее распространение на практике имеют плоские кинематические цепи.

По виду звеньев, входящих в кинематические цепи, последние разделя­ются на простые и сложные.

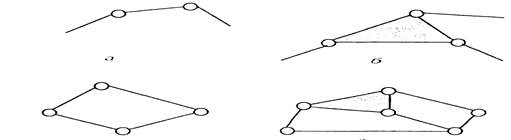
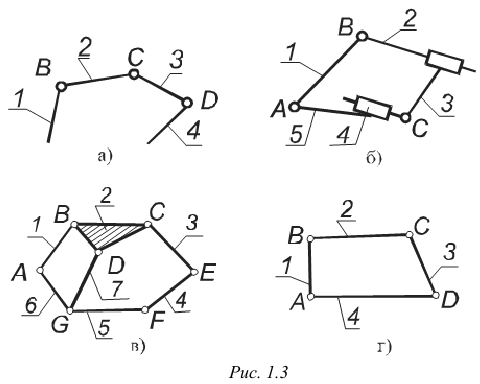
Простой кинематической цепью называется такая цепь, в которой каж­дое звено участвует в образовании не более двух кинематических пар (рис. 1.3, а).

Сложной кинематической цепью называется цепь, в которой имеется хотя бы одно звено, входящее более чем в две кинематические пары (рис. 1.3, б).

Все кинематические цепи, кроме того, подразделяются на незамкнутые и замкнутые.

Незамкнутыми кинематическими цепями называют такие цепи, в которых имеются звенья, образующие только одну кинематическую пару (см. рис. 1.3, а, б).

Рис. 1.3

Замкнутыми называ­ются кинематические цепи, в которых каждое звенообразует не менее чем две кинематические пары (рис. 1.3, в, г).

В технике обычно интересует движение звеньев кинематической цепи относительно одного из звеньев, которое является неподвижным и называется стойкой. Если одно звено кинематической цепи сделать неподвижным, то число степеней свободы уменьшится еще на три и относительно неподвижно­го звена (стойки) будет равно

W = H – 3 = 3(k–1) – 2p1 – p2 (1.2)

где W – число степеней свободы кинематической цени относительно неподвижного звена.

Обозначив к-1= п (количество подвижных звеньев кинематической цепи), окончательно получим выражение для числа степеней свободы кине­матической пени относительно неподвижного звена

Число степеней свободы кинематической цепи IV относительно непод­вижного звена (стойки) называется степенью подвижности кинематической цепи. Формула (1.3) впервые была получена русским ученым П. Л. Чебышевым и носит его имя. Следует отметить, что эта формула пригодна только для определения степени подвижности плоских кинематических цепей.

Механизмы

Дадим определение механизма на основании понятия о кинематической цепи. Предварительно отметим, что звенья кинематической цепи, законы движения которых являются заданными, называются ведущими, остальные звенья называются ведомыми.

Механизмом называется кинематическая цепь с одним неподвижным звеном (стопкой), в которой при заданном законе движения одного или нескольких ведущих звеньев все остальные (ведомые) звенья движутся вполне определенным образом.

Рассмотрим условия, при которых кинематическая цепь будет механиз­мом. Известно, что точка на плоскости имеет две степени свободы и для оп­ределения ее положения необходимо задать две координаты. В случае твер­дого тела, имеющего при плоском движении три степени свободы, для одно­значного определения его положения необходимо знать три координаты: две координаты точки, выбранной за полюс, и угол поворота некоторого отрезка, соединяющего две точки тела.

Аналогично и для кинематической цепи. Чтобы положения всех звень­ев кинематической цепи относительно стойки были вполне определенными, необходимо задать столько параметров, сколько степеней подвижности (степеней свободы относительно стойки) имеет кинематическая цепь. Параметры, которые задаются кинематической цепи, определяются заданным законом движения ведущего звена (или ведущих звеньев). Поэтому, чтобы движения ведомых звеньев кинематической цепи были вполне определенными, необходимо, чтобы количество ведущих звеньев цепи было равно степени подвижности этой цепи. Только в этом случае кинематическая цепь является механизмом.

В 1916 г. профессором Петербургского политехнического института Л. В. Ассуром был предложен следующий принцип образования механизмов: любой механизм может быть образован путем непосредственного присоединения («наслоения») сначала к ведущему звену и стойке, а затем и к любым другим звеньям кинематических цепей с нулевой степенью подвижности.

В самом деле, присоединение к ведущему звену кинематических цепей с путевой степенью подвижности (W = 0) не изменит общей степени подвиж­ности механизма.

Кинематические цепи, обладающие нулевой степенью подвижности (степенью свободы относительно стойки), называются группами Аcсура. Все разнообразие групп Аcсура можно получить из формулы Чебышева.

Будем полагать, что кинематическая цепь состоит лишь из пар 1-го класса. Тогда для группы Аcсура с нулевой степенью подвижности (W = 0) получим

Так как количество звеньев и кинематических пар может быть только целым числом, то количество звеньев группы Ассура может быть только четным числом. Следовательно, равенству (1.5) могут удовлетворять следующие числа подвижных звеньев п и кинематических пар 1-го класса р1.

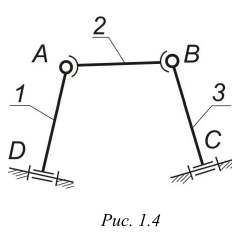
Рис. 1.4

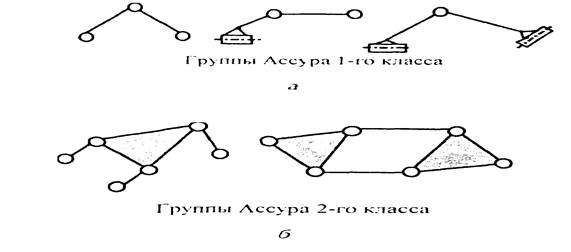
В зависимости от количества звеньев и числа кинематических пар опре­деляется класс группы Ассура. Так, кинематическая цепь с количеством звеньев п = 2 и количеством кинематических пар р1 = 3 является группой Ассура 1-го класса. При п = 2 и р₁ = 3 будем иметь группу Ассура 2-го класса и т. д.

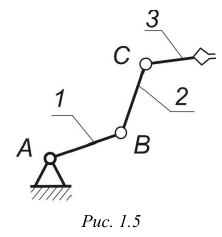
Примеры групп Ассура 1-го и 2-го классов представлены на рис. 1.5, а, 6.

Если присоединить любую группу Ассура к стойке, то получим кинематическую цепь с нулевой степенью подвижности, т. е. ферму (рис. 1.6, а), а если присоединить ее внешними кинематическими парами к ведущему звену и к стойке или к новым звеньям первоначального механизма, то получим новый механизм, степень подвижности которого не изменится (рис. 1.6, б).

Рис 1.5

В соответствии со строе­нием механизмы делятся на классы. Класс механизма за­висит от классов групп Ас­сура, входящих в его состав. Если в состав механизма входят группы Ассура раз­личных классов, то номер класса механизма определя­ется номером класса наи­высшей группы Ассура. На рис. 1.6. б изображен меха­низм, в состав которого входят группы Ассура 1-го и 2-го классов. Исходя из сказан­ного выше, данный меха­низм является механизмом 2-го класса.

Механизмы, не содержащие групп Ассура, а состоящие только из ведущего звена, относятся к механизмам нулевого класса. Такие механизмы встречаются на практике довольно часто. К ним, например, относятся механизмы электродвигателей, генераторов и так далее.

Рассмотренная классификация механизмов не является единственной. Существуют также другие виды классификаций. Широко ис­пользуется практическая классификация механизмов, ко­торая в общих чертах учитывает основные кинематические свойства и конст­руктивные особенности механизмов, а в отдельных случаях и функциональ­ное назначение.

В соответствии с практической классификацией механизмы делятся на следующие виды:

а) зубчатые передачи;

б) фрикционные передачи;

в) передачи с гибкой связью;

г) винтовые механизмы;

д) кулачковые механизмы;

е) рычажные механизмы;

ж)механизмы прерывистого действия;

з)электромагнитный механизмы и др.

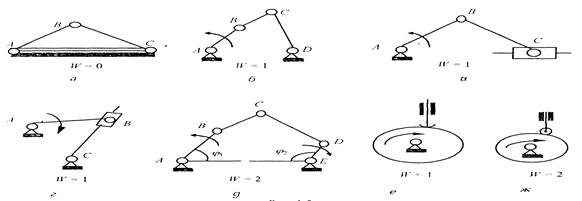
На рис. 1.7 представлены кинематические схемы механизмов в соответствии с практической классификацией:

фрикционные механизмы: цилиндрический (а) и конический с постоянным передаточным отношением (б), с переменным передаточным отношением (в):

кулачковые механизмы: с поступательно движущимся (г) и качающимся (д) толка гелем;

Источник

Кинематические цепи и кинематическая схема механизма

Кинематической цепью называется связанная система звеньев, образующих между собой кинематические пары.

Кинематические цепи делятся на простые и сложные.

Простой кинематической цепью называется такая цепь, у которой каждое звено входит не более чем в две кинематические пары.

Сложной кинематической цепью называется цепь, в которой имеется хотя бы одно звено входящее более чем в две кинематические пары.

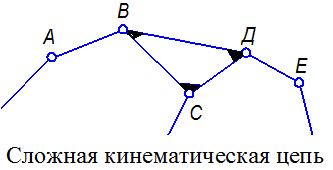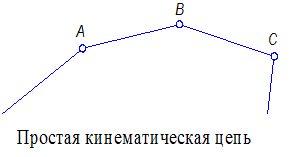Рис. 1.3

Простые и сложные кинематические цепи делятся на замкнутые и незамкнутые.

Замкнутой кинематической цепью называется цепь, каждое подвижное звено которой входит, по крайней мере, в две кинематические пары (Рис. 1.4а).

Незамкнутой кинематической цепью называется цепь, в которой есть звенья, входящие только в одну кинематическую пару (Рис. 1.4б).

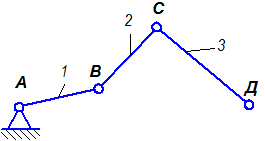а) Замкнутая	б) Незамкнутая
Рис. 1.4

Кинематической схемой механизма называется его изображение в выбранном масштабе с применением условных обозначений, установленных ГОСТом, звеньев и кинематических пар.

Схема позволяет определить движение ведомых звеньев по заданному движению ведущих.

АВ – ведущее звено, т.е звено движение которого задано.

Источник

Кинематические цепи

Кинематические цепи

Кинематическая цепь — это связанная система звеньев, соединенных между собой кинематическими парами. Кинематические цепи можно разделить на плоские и пространственные, простые и сложные, замкнутые и незамкнутые (рис. 1.3). К простым относятся цепи, у которых каждое звено входит не более чем в две кинематические пары (рис. 1.3, а, г); к сложным — цепи, у которых имеются звенья, входящие в три и болей кинематические пары (рис. 1.3, в); к замкнутым — цепи, у которых каждое звено входит, по крайней мере, в две кинематические пары (рис. 1.3, б, г), к незамкнутым — цепи, у которых есть звенья, входящие только в одну кинематическую пару (рис. 1.3, а). Все подвижные звенья плоской кинематической цепи совершают движения, параллельные одной и той же неподвижной плоскости (см. рис. 1.1). В пространственных кинематических цепях точки звеньев описывают пространственные кривые либо жутся по плоским кривым, лежащим в пересекающихся плоскостях (рис. 1.4).

Введя понятие кинематической цепи, можно дать другое определение для механизмов, составленных только из твердых тел. Механизмом называется кинематическая цепь, в которой при одном неподвижном звене (стойке) и заданном движении одного или нескольких звеньев (ведущих) все остальные звенья (ведомые) совершают однозначно определенные движения. Механизмы могут быть образованы как замкнутыми, так и незамкнутыми кинематическими цепями. Примером незамкнутой кинематический цепи может служить механизм элементарного манипулятора (рис. 1.5). Большинство механизмов образовано замкнутыми кинематическими цепями 3 (см. рис. 1.1, 1.4).

При исследовании механизмов используются их условные изображения, составляются структурные, кинематические и другие схемы. Структурные схемы выполняются в виде чертежа, на котором с учетом условных обозначений, установленных ГОСТом, изображают звенья, кинематические пары, указывают стойку и ведущие звенья (см. рис. 1.1). Структурные схемы, выполненные в определенном масштабе, называются кинематическими схемами.

Эта теория взята со страницы лекций по предмету «прикладная механика»:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник