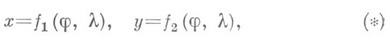Что называется картографической проекцией
Картографические проекции. Урок 6
Картографические проекции сегодня – это математические способы изображения всего земного эллипсоида или его части на плоскости, систематическое преобразование широт и долгот с поверхности сферы на плоскость.
Для создания географических карт выполняют две последовательных операции:
При этом картографы пытаются добиться как можно меньшего количества искажений. Сделать мелкомасштабную карту совсем без искажений невозможно. На крупномасштабных (топографических) картах искажения почти отсутствуют. В зависимости от назначения карты одни погрешности допустимы, другие нет. Поэтому и существуют разные типы проекций, предназначенные для сохранения некоторых свойств сферы за счёт других её свойств.

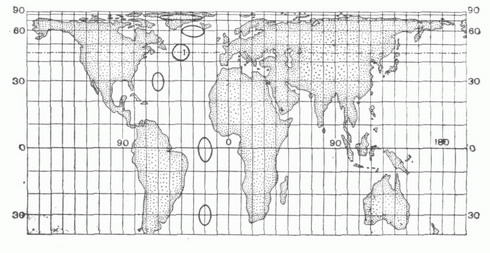
Виды искажений при использовании картографических проекций
Разложить на плоскости эллипс или шар очень трудно, для того, чтобы убедиться в этом, можно попробовать это сделать на практике. Сложить кусочки апельсиновой кожуры так, чтобы между ними не было пустых мест и попробовать получить непрерывную ровную плоскость. Корка соберётся в складки, она не уложится без промежутков.
При любом способе разложения шара на плоскость присутствует один или несколько типов искажения:
При этом типы искажений взаимозависимы, при уменьшении одного из показателей увеличивается другой. В зависимости от назначения карты, на ней присутствуют места с нулевым искажением, с удалением от него количество искажений увеличивается. Поэтому на карте есть три вида масштаба:
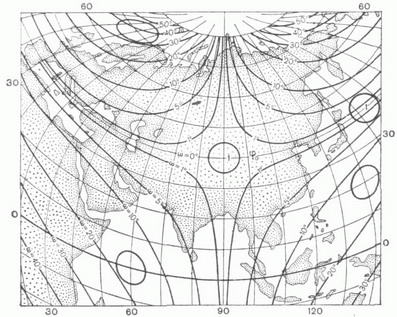
При выборе типа картографической проекции сначала строят изоколы – изолинии, соединяющие точки с одинаковым искажением.

Источник: https://ds04.infourok.ru/uploads/ex/0617/00148bfe-04623ef1/hello_html_329bd6b7.jpg
Типы проекций по характеру искажений
Для разных целей нужны карты с отсутствием тех или иных видов искажений. При помощи разных проекций можно сделать так чтобы на них отсутствовали погрешности либо углов, либо длин, либо площадей. Чем больше искажаются углы, тем меньше искажаются площади и наоборот. По характеру искажений все картографические проекции делят на:
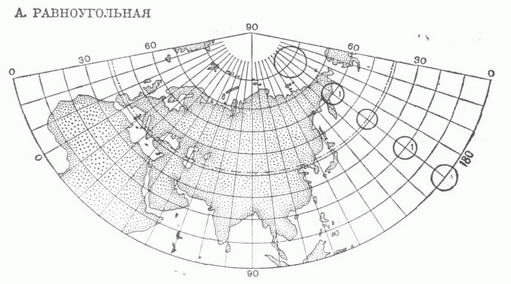
Равноугольные картографические проекции
На картах, построенных по этому типу, нет искажений направлений и углов. Направления на местности совпадают с таковыми на карте, прямые линии на местности остаются прямыми на карте. Они используются для прокладки точных маршрутов и применяется на навигационных и топографических картах.
Зато на них сильно изменены площади объектов Земли и линейный масштаб карты зависит от положения на ней данной точки. Типичный пример равноугольной проекции – цилиндрическая проекция Герхарда Меркатора (Герарда Кремера), созданная ещё в 1569 г и используемая в морской навигации до сих пор. Примером использования Проекции Меркатора является равноугольная проекция Гаусса-Крюгера.
В этой проекции создаются отдельные океанологические, климатические и геофизические карты.

Файл доступен по лицензии: Creative Commons Attribution-Share Alike 3.0 Unported
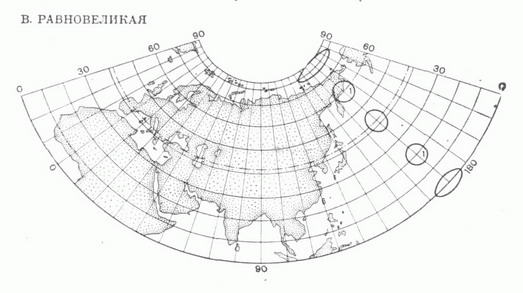
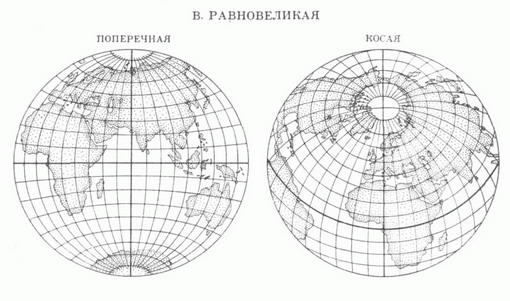
Равновеликие картографические проекции
Это проекции для построении карт, на которых нет искажения площадей (масштаб площадей имеет везде одну и ту же величину), зато сильно растёт погрешность форм и углов (материки и океаны в высоких широтах сплющиваются). Картами, построенными в равновеликих проекциях, удобно пользоваться для расчета площадей, например типов почв, посадок кукурузы, облесенности материков, загрязнения океана или радиоактивного загрязнения суши и др.
Их применяют для составления климатических, почвенных, геофизических, геологических, зоогеографических, геоботанических, экономических, исторических, этнографических, административных карт.

Произвольные картографические проекции
Углы и площади здесь искажаются, но значительно меньше, чем в предыдущих двух проекциях. Поэтому они наиболее используемы. Произвольные картографические проекции не относятся ни к равновеликим, ни к равноугольным.

Равнопромежуточные картографические проекции
Это тип произвольных картографических проекций. В них масштаб длин одного из главных направлений остаётся неизменным. Пример: прямая азимутальная проекция. Равнопромежуточные проекции используют для создания общегеографических, физических, тектонических, политических и др. видов карт.
Характер искажения всегда входит в общее название проекции (равновеликая азимутальная, равноугольная коническая, равновеликая цилиндрическая и т.д.).
Интересно,
что д ревнейшей картографической проекцией является гномическая проекция, применённая на картах звёздного неба Фалесом Милетским ещё в Древней Греции.

Классификация географических проекций по геометрической фигуре, являющейся вспомогательной поверхностью
На плоскость эллипсоид проектируют при помощи геометрических фигур, а поверхности, на которые он проектируется, могут быть секущими (разрезающей) фигуру или касательными (соприкасается, но не разрезает глобус) к ней. При этом на полученной карте касательные и секущие линии (стандартные) представлены неискажёнными.
Проекции также бывают по-разному ориентированы.
Поверхности, которые могут быть развёрнуты на плоскость или лист без растяжений, разрыва или усадки, называются разрабатываемыми поверхностями. Ими являются цилиндр, конус и плоскость. Поэтому по вспомогательной поверхности проекции делятся на:
Полное название проекций может быть следующим: косая азимутальная равновеликая, нормальная равноугольная цилиндрическая, произвольная поликоническая и т.д.
Картографические проекции
Полезное
Смотреть что такое «Картографические проекции» в других словарях:
КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ — математические способы изображения на плоскости поверхности земного эллипсоида или шара. Картографические проекции определяют зависимость между координатами точек на поверхности земного эллипсоида и на плоскости. Из за невозможности развернуть… … Большой Энциклопедический словарь
КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ — КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ, системные методы нанесения меридианов и параллелей Земли на плоскую поверхность. Только на глобусе можно достоверно представить территории и формы. На плоских картах больших территорий искажения неизбежны. Проекции это… … Научно-технический энциклопедический словарь
КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ — математический способ отображения земной поверхности, принимаемой за эллипсоид или шар, на плоскости. Картографические Проекции позволяют учитывать возникающие при этом неизбежные искажения. Картографические Проекции можно задать аналитически или … Морской энциклопедический справочник
картографические проекции — математические способы изображения на плоскости поверхности земного эллипсоида или шара. Картографические проекции определяют зависимость между координатами точек на поверхности земного эллипсоида и на плоскости. Из за невозможности развернуть… … Энциклопедический словарь
КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ — матем. способы изображения на плоскости поверхности земного шара (эллипсоида). К. п. определяют зависимость между координатами точек на поверхности земного эллипсоида и на плоскости. Из за невозможности развернуть поверхность эллипсоида на… … Большой энциклопедический политехнический словарь
КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ — матем. способы изображения на плоскости поверхности земного эллипсоида или шара. К. п. определяют зависимость между координатами точек на поверхности земного эллипсоида и на плоскости. Из за невозможности развернуть поверхность эллипсоида (или… … Естествознание. Энциклопедический словарь
КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ КАРТ АТЛАСА — Поверхность земного шара (эллипсоида) нельзя изобразить на плоскости (в данном случае на карте) без искажений, т. е. таким образом, чтобы масштабы длин оставались постоянными на всех участках карты и по всем направлениям. При мелкомасштабном… … Географический атлас
ИЗОБРАЖЕНИЕ ШАРОВОЙ ПОВЕРЗНОСТИ НА ПЛОСКОСТИ (КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ) — Изображение шаровой поверзности на плоскости (картографические проекции) … Географический атлас
Проекции картографические — см. Картографические проекции … Большая советская энциклопедия
Картографические приборы — приборы, применяемые при составлении и оформлении (подготовке к изданию) карт. При составлении математической основы (картографической сетки и опорных пунктов) применяются Координатографы, штангенциркули (См. Штангенциркуль) с линейками… … Большая советская энциклопедия
КАРТОГРАФИЧЕСКАЯ ПРОЕКЦИЯ
— отображение всей поверхности земного эллипсоида или какой-либо ее части на плоскость, получаемое в основном с целью построения карты.
В картографии часто ограничиваются рассмотрением отображений на плоскость сферы нек-рого радиуса R, отклонениями к-рой от земного эллипсоида можно пренебречь или каким-либо способом их учесть. Поэтому далее имеются в виду отображения на плоскость хОу сферы, отнесенной к географич. координатам j (широта) и X(долгота).
Уравнения К. п. имеют вид
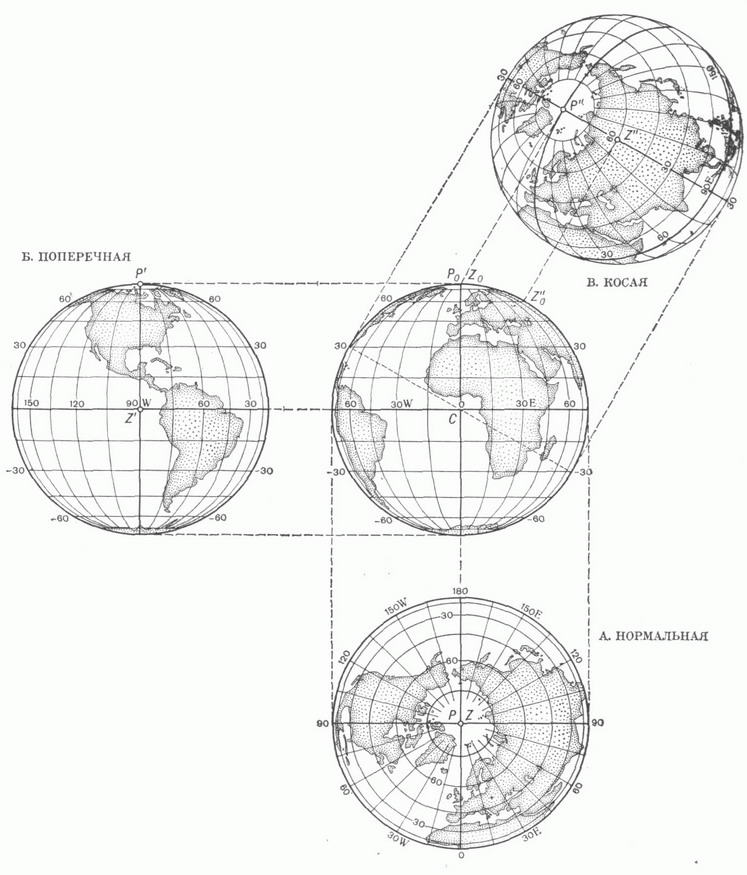
1. СЕТИ СФЕРИЧЕСКИХ КООРДИНАТНЫХ ЛИНИЙ
2. ШАР И ЕГО ОРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ
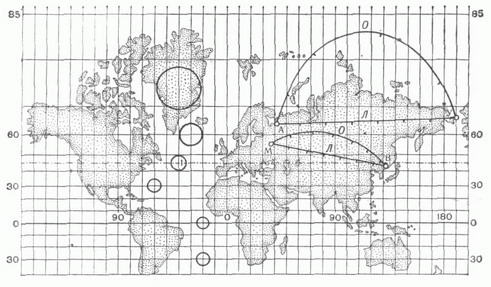
3. ЦИЛИНДРИЧЕСКИЕ ‘ ПРОЕКЦИИ
А. РАВНОУГОЛЬНАЯ МЕРКАТОРА
Б. РАВНОПРОМЕЖУТОЧНАЯ (ПРЯМОУГОЛЬНАЯ)
В. РАВНОВЕЛИКАЯ (ИЗОЦИЛИНДРИЧЕСКАЯ)
4. КОНИЧЕСКИЕ ПРОЕКЦИИ
5. АЗИМУТАЛЬНЫЕ ПРОЕКЦИИ
6. ПСЕВДОКОНИЧЕСКАЯ РАВНОВЕЛИКАЯ ПРОЕКЦИЯ БОННА
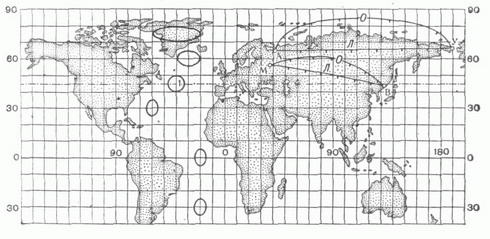
7. КОСАЯ ПЕРСПЕКТИВНО-ЦИЛИНДРИЧЕСКАЯ ПРОЕКЦИЯ М.
Полезное
Смотреть что такое «КАРТОГРАФИЧЕСКАЯ ПРОЕКЦИЯ» в других словарях:
картографическая проекция — проекция Математически определенный способ отображения поверхности шара или эллипсоида на плоскость, используемый для создания картографического произведения. [ГОСТ 21667 76] Тематики картография Обобщающие термины математическая картография… … Справочник технического переводчика
картографическая проекция — Математический способ изображения, а также собственно изображение поверхности эллипсоида или шара на плоскости географической карты … Словарь по географии
Картографическая проекция — Пример картографической проекции проекция Меркатора Картографическая проекция математически определенный способ отображения поверхности эллипсоида на плоскости. Суть проекций связана с тем, что фигуру Земли … Википедия
картографическая проекция — математически определённое отображение поверхности земного шара, эллипсоида (или глобуса) на плоскость карты. Проекция устанавливает соответствие между географическими координатами точки (широтой В и долготой L) и её прямоугольными координатами… … Географическая энциклопедия
псевдоазимутальная картографическая проекция — картографическая проекция Картографическая проекция, в которой параллели нормальной сетки концентрические окружности или их дуги, а меридианы кривые, исходящие из центра параллелей, симметричные относительно одного или двух прямолинейных… … Справочник технического переводчика
равновеликая картографическая проекция — равновеликая проекция Н.д.п. авталическая проекция гомолографическая проекция равноплощадная проекция эквивалентная проекция Картографическая проекция, в которой отсутствуют искажения площадей. [ГОСТ 21667 76] Недопустимые, нерекомендуемые… … Справочник технического переводчика
равноугольная картографическая проекция — равноугольная проекция Ндп. конформная проекция ортоморфная проекция изогональная проекция автогональная проекция Картографическая проекция, в которой отсутствуют искажения углов. [ГОСТ 21667 76] Недопустимые, нерекомендуемые автогональная… … Справочник технического переводчика
азимутальная картографическая проекция — азимутальная проекция Ндп. зенитальная проекция Картографическая проекция, в которой параллели нормальной сетки концентрические окружности, а меридианы их радиусы, углы между которыми равны соответствующим разностям долгот. [ГОСТ 21667 76]… … Справочник технического переводчика
равнопромежуточная картографическая проекция — равнопромежуточная проекция Ндп. эквидистантная проекция Произвольная картографическая проекция, в которой масштаб по одному из главных направлений постоянная величина. [ГОСТ 21667 76] Недопустимые, нерекомендуемые эквидистантная проекция… … Справочник технического переводчика
коническая картографическая проекция — коническая проекция Картографическая проекция, в которой параллели нормальной сетки дуги концентрических окружностей, а меридианы их радиусы, углы между которыми пропорциональны соответствующим разностям долгот. [ГОСТ 21667 76] Тематики… … Справочник технического переводчика
Картографическая проекция
Содержание
КАРТОГРАФИЧЕСКАЯ ПРОЕКЦИЯ И ЕЁ ВИДЫ
Обоснование выбора темы параграфа
Для своей работы мы выбрали тему «Картографические проекции». В настоящее время в учебниках географии данная тема практически не рассматривается, сведения о различных картографических проекциях можно увидеть только в атласе 6 класса. Мы считаем, что учащимся будет интересно знать, по каким принципам выбираются и строятся различные проекции географических карт. Вопросы о картографических проекциях часто затрагиваются в олимпиадных заданиях. Встречаются они и на ЕГЭ. Кроме того, карты атласов, как правило, построены в разных проекциях, что вызывает вопросы у учащихся.Картографическая проекция является основой для построения карт. Тем самым, знание основных принципов построения картографических проекций пригодится учащимся при выборе профессий летчика, моряка, геолога. В связи с этим, мы считаем целесообразным включить данный материал в учебник географии. Поскольку на уровне 6 класса математическая подготовка учащихся еще не такая сильная, на наш взгляд, имеет смысл изучать данную тему в начале 7го класса в разделе «Общие особенности природы Земли» при рассмотрении материала об источниках географической информации.
Картографические проекции
Географическую карту невозможно представить себе без системы параллелей и меридиан, формирующих её градусную сеть. Именно они позволяют нам точно определить местоположение объектов, именно по ним определяются стороны горизонта на карте. Даже расстояния по карте возможно вычислить с помощью градусной сети. Если посмотреть на карты в атласе, можно заметить, что градусная сеть на разных картах выглядит по-разному. На одних картах параллели и меридианы пересекаются под прямым углом и представляют собой сетку из параллельных и перпендикулярных прямых. На других картах меридианы веером расходятся из одной тоски, а параллели представлены в виде дуг. На карте Антарктиды меридианы похожи на снежинку, а параллели отходят от центра концентрическими кругами.
СОЗДАНИЕ КАРТ
Виды проекций
Что же собой представляет картографическая проекция?
Картографи́ческая прое́кция — математически определенный способ отображения поверхности эллипсоида на плоскости. Принятая при данной картографической проекции система изображения сети меридианов и параллелей называется картографической сеткой.
По способу построения картографической нормальной сетки все проекции делятся на конические, цилиндрические, условные, азимутальные, и др.
На цилиндрических проекциях получение нормальной сетки осуществляется путем проектирования её на стенки цилиндра, ось которого совпадает с Земной осью. Затем его разворачивают на плоскость. Сетка получают из взаимно перпендикулярных прямых линий параллелей и меридианов.
На азимутальных проекциях нормальная сетка получается сразу на плоскости проекции. Для этого центр плоскости совмещается с полюсом Земли. В результате параллели имеют вид концентрических окружностей, радиус которых увеличивается по мере удаления от центра, а меридианы выглядят прямыми, пересекающимися в центре.
Условные проекции строятся по каким-либо заранее поставленным условиям. Эту категории нельзя отнести к другим видам проекции. Их число неограниченно.
Конечно, перенести изображение с поверхности шара на плоскость абсолютно точно невозможно. Если мы попробуем это сделать, неизбежно получим разрыв в изображении. Тем не менее, на карте мы этих разрывов не видим, да и при переносе изображения на поверхности цилиндра, конуса или плоскость изображение получается единым. В чем же дело?
Проецируя точки с поверхности Земного шара на поверхности будущей карты, мы получаем искаженные изображения. Если представить проектирование поверхности Земли на плоскость в виде тени, которая получится при подсвечивании объекта из центра Земли, то чем дальше объект от места непосредственного соприкосновения поверхности карты с шаром, тем больше изменится его изображение.
По характеру искажений все проекции делят на равноугольные, равновеликие и произвольные.
На равноугольных проекциях углы на местности между какими-либо направлениями равны углам на карте между теми же направлениями, то есть они(углы) не имеют искажений. Масштаб зависит только от положения точки и не зависит от направления. Угол на местности всегда равен углу на карте, линия, прямая на местности — прямая на карте. Бесконечно малые фигуры на карте в силу свойства равноугольности будут подобны тем же фигурам на Земле. Но линейные размеры на картах этой проекции будут иметь искажения.Представьте себе идеально круглое озеро.В каком бы месте полученной карты оно ни располагалось, его форма останется круглой, а вот размеры могут существенно измениться. Русло реки будет изгибаться так же, как изгибается на местности, но расстояние между его изгибами не будет соответствовать реальному.
На равновеликих проекциях не искажаются площади, сохраняется их пропорциональность. Но сильно искажены углы и формы. При перенесении его очертаний на карту в месте соприкосновения шара и поверхности будущей карты, его изображение будет таким же круглым. В то же время, чем дальше оно будет расположено от линии соприкосновения, тем больше будут вытягиваться его очертания, хотя площадь озера будет неизменной.
На произвольных проекциях искажены и углы, и площади, не сохранятся подобие фигур, но имеют какие-либо специальные свойства, не присущие другим проекциям, поэтому они наиболее употребляемые.
Карты создаются либо непосредственно в результате топографических съемок местности, либо на основе других карт, то есть, в конечном счете, опять-таки в результате съемки. В настоящее время, подавляющее большинство топографических карт создастся с помощью метода аэрофотосъемки, который позволяет в короткий срок получить топографическую карту огромной территории. С летящего самолета с помощью особых фотографических аппаратов делается много снимков (аэрофотоснимки) местности. Потом эти аэрофотоснимки обрабатывают на специальных приборах. Прежде чем стать картой, серия аэрофотоснимков проходит в производстве длинный и сложный путь.
Все мелкомасштабные общегеографические и специальные карты (в том числе и электронные GPS карты) создаются на основе других карт, только более крупного масштаба.
Термины
Вопросы
1. Что такое картографическая проекция? 2. Какие виды картографических проекций вы знаете? 3. Какой раздел картографии занимается созданием проекций? 4. От чего зависит характер искажений на карте?
Поработайте дома
1.Заполните в тетради таблицу, отражающую характеристики различных картографических проекций.
| Азимутальная проекция | Коническая проекция | Цилиндрическая проекция |
|---|---|---|
| Основа для построения проекции | ||
| Как показаны меридианы | ||
| Как показаны параллели | ||
| Максимальные искажения | ||
| Минимальные искажения | ||
| Для каких карт используется |
2.Определите, в каких проекциях построены карты атласа. Какой вид проекции использовался чаще? Почему?
Задание для любознательных
Пользуясь дополнительными источниками информации, найдите, в какой проекции построена карта полушарий.
Информационные ресурсы для углубленного изучения данной темы
Литература по теме
НАВИГАЦИЯ. Глава 3. §19 Классификация картографических проекций.
§19 Классификация картографических проекций.
Картографические проекции можно классифицировать по различным признакам. Однако с точки зрения построения и практического использования карт, наиболее употребительными признаками их классификации служат:
• характер искажений проекций, обусловливающий возможности практического использования карт;
• вид меридианов и параллелей нормальной сетки.
По характеру искажений
все картографические проекции делятся на четыре группы:
• равноугольные, или конформные;
• равновеликие, или эквивалентные (равноплощадные);
Равноугольные проекции
Основным свойством равноугольных, или конформных, проекций является сохранение подобия малых фигур на карте соответствующим фигурам на поверхности Земли.
Равноугольные проекции не искажают углов. Бесконечно малый круг на такой проекции изображается также кругом.
Однако, при сохранении неискаженными углов и направлений, в равноугольной проекции искажаются линейные размеры и площади фигур. Масштаб в таких проекциях зависит от направления. Эллипсы искажений, обращаясь во всех точках карты в окружности, имеют размеры, зависящие от положения точки.
Постоянство частного масштаба в данной точке по всем направлениям облегчает производство измерений на карте, составленной в равноугольной проекции. Для учета изменения масштаба при измерении больших отрезков их следует измерять на карте по частям.
Свойство конформности позволяет на картах, составленных в таких проекциях, измерять углы и азимуты непосредственно с помощью транспортира. Эти свойства обусловили широкое применение равноугольных проекций для построения морских карт. Отметим, что равноугольные проекции сохраняют равными углы, но не кривизну линий, поэтому подобие сохраняется только для малых фигур.
К равноугольным проекциям относятся проекции Меркатора, Гаусса, стереографическая и некоторые другие.
Равновеликие проекции
Равновеликие, или эквивалентные, проекции не обладают свойством подобия фигур, но сохраняют масштаб площадей в пределах всей карты одинаковым. Это означает, что равным между собой площадям на местности соответствуют равные между собой площади на карте.
Бесконечно малый на местности изобразится на карте в равновеликой проекции эллипсом, площадь которого равна площади кружка на глобусе. Любая замкнутая фигура произвольных размеров на глобусе изобразится на проекции не подобной, но равновеликой ей замкнутой фигурой. Формы эллипсов искажений в разных точках карты будут различными, площади же их обязательно будут равны площадям соответствующих кружков на глобусе.
На картах, составленных в равновеликих проекциях, можно измерять площади и сопоставлять их. Свойство равновеликости сохраняется независимо от размеров картографируемых участков. Поэтому измерения можно производить и на больших площадях.
Равнопромежуточные проекции
Равнопромежуточными называются проекции, сохраняющие постоянство масштаба по одному из главных направлений.
Вследствие этого бесконечно малый круг поверхности глобуса изобразится на плоскости проекции эллипсом, у которого одна из осей, сохранив величину, останется равной радиусу этого круга.
Произвольные проекции
Проекции, не относящиеся ни к одной из рассмотренных групп, но обладающие какими-либо другими, важными для практики свойствами, называются произвольными.
К числу наиболее часто используемых, произвольных проекций можно отнести центральную перспективную проекцию, на которой дуги больших кругов изображаются прямыми линиями.
По виду меридианов и параллелей нормальной картографической сетки
проекции делятся на следующие основные группы:
Из всех перечисленных здесь рассматриваются лишь те виды проекций, которые используются или могут использоваться для построения морских карт.
Конические проекции
Коническими называются проекции, у которых меридианы нормальной сетки изображаются прямыми, сходящимися в общей точке под углами, пропорциональными разности долгот, а параллели нормальной сетки изображаются концентрическими окружностями, имеющими общий центр в точке пересечения меридианов.
Название конических такие проекции получили оттого, что они могут быть получены не только аналитически, но и путем геометрического проектирования поверхности глобуса на поверхность касательного или секущего глобус конуса, ось которого совпадает с географической осью глобуса.
Проектирование при этом осуществляется из точки зрения, находящейся на оси конуса. На параллели, по которой поверхность конуса касается глобуса (а также на параллелях сечения глобуса конусом), масштаб равен единице. С удалением от параллели касания в обе стороны масштаб возрастает. При проектировании на секущий конус масштаб между параллелями сечения будет меньше масштаба глобуса. т. е. меньше главного масштаба.
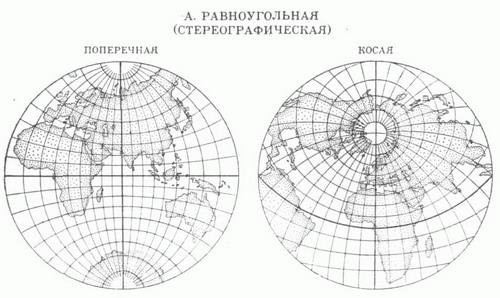
Азимутальные проекции
Азимутальными называются проекции, у которых меридианы нормальной сетки изображаются прямыми линиями, исходящими из общего центра, под углами, равными соответствующим углам между меридианами на глобусе, а параллели имеют вид концентрических окружностей с центром в точке схождения меридианов
Из приведенного определения видно, что азимутальные проекции являются частным случаем конических проекций.
Точка схождения меридианов в азимутальных проекциях является изображением полюса нормальной системы координат. Свойствами азимутальных проекций являются: равноугольность, равновеликость или равнопромежуточность.
К классу азимутальных проекций относятся перспективные проекции, получающиеся путем проектирования точек поверхности глобуса (шара) на картинную плоскость лучами, исходящими из постоянной точки.
Эта точка называется точкой зрения.
Картинная плоскость может или касаться поверхности проектируемого глобуса, или находиться от него на некотором удалении, или пересекать ее. Точка зрения выбирается на перпендикуляре к картинной плоскости, проходящем через центр проектируемого глобуса.
В зависимости от расположения точки зрения относительно центра глобуса перспективные проекции делятся:
— на ортографические, когда точка зрения удалена в бесконечность;
— на внешние, когда точка зрения находится на конечном расстоянии от центра проектируемого глобуса, но далее точки, представляющей антипод полюса нормальной системы координат;
— на стереографические, когда расстояние от центра глобуса до точки зрения равно радиусу глобуса, т.е. когда точка зрения помещается в точке шара, противоположной полюсу нормальной системы координат (в точке — антиподе полюса нормальной системы координат);
— на центральные (гномонические), когда точка зрения помещена в центре глобуса.
Цилиндрические проекции
Цилиндрическими проекциями называются такие, параллели и меридианы нормальной сетки которых изображаются взаимно перпендикулярными прямыми.
Удаление параллелей сетки от экватора является функцией широты, расстояния между меридианами пропорциональны разностям долгот.
Общие уравнения цилиндрических проекций имеют вид:
x = f (φ); y = C λ
Вид функции x = f (φ) и коэффициент С определяют важнейшие свойства цилиндрической проекции. Изменяя их, можно получить равноугольную, равнопромежуточную, равновеликую или произвольную проекцию. Цилиндрические проекции могут быть получены путем проектирования поверхности глобуса на касательный или секущий глобус цилиндр. При проектировании на касательный по экватору цилиндр масштаб вдоль экватора сохраняет равенство главному масштабу, т.е. экватор глобуса изображается на проекции без искажений. При проектировании на секущий цилиндр линиями нулевых искажений будут являться параллели сечения.
Из цилиндрических наиболее употребительны в кораблевождении прямая и поперечная проекции Меркатора и поперечная проекция Гаусса.