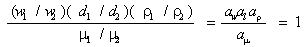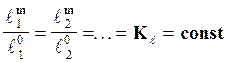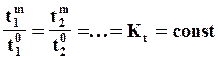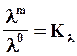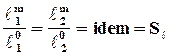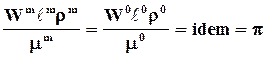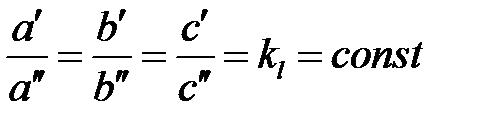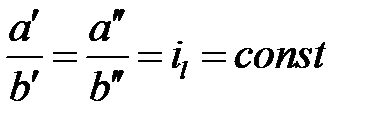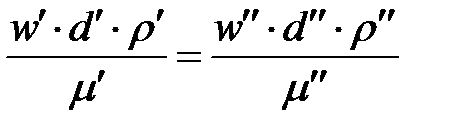Что называется инвариантом подобия

инвариант подобия

Смотреть что такое «инвариант подобия» в других словарях:

ИНВАРИАНТ МАТРИЦЫ — характеристика квадратной матрицы А, сохраняющаяся при преобразовании подобия A =S 1AS, где S невырожденная матрица (её определитель отличен от нуля, detS№0). Матрицы А и А наз. подобными. Алгебраич. матричные ур ния сохраняют свой вид при… … Физическая энциклопедия

число подобия — число подобия; инвариант подобия Безразмерный степенной комплекс, составленный из величин, существенных для данного процесса … Политехнический терминологический толковый словарь

ДИКСОНА ИНВАРИАНТ — конструкция, используемая при изучении квадратичных форм над полями характеристики 2, позволяющая, в частности, вводить аналоги специальной ортогональной группы над такими полями. А именно, Д. и. есть элемент D(u)произвольного поля… … Математическая энциклопедия

інварiант подібностi — инвариант подобия similarity invariant Ähnlichkeitsinvariante, Ähnlichkeitssimplex Див. симплекс подiбностi … Гірничий енциклопедичний словник

ИНТЕГРАЛЬНАЯ ГЕОМЕТРИЯ — теория инвариантных (относительно непрерывных групп отображений пространства на себя) мер на множествах, состоящих из подмногообразий пространства (напр., прямых, плоскостей, геодезических, выпуклых поверхностей и т. п. многообразий, сохраняющих… … Математическая энциклопедия

ТУРБУЛЕНТНОСТЬ ПЛАЗМЫ — явление, родственное обычной турбулентности, но осложнённое специфич. хар ром кулоновского вз ствия ч ц плазмы (эл нов и ионов). Поскольку для плазмы характерно большое разнообразие разл. типов движений и колебаний, в ней могут возникать и даже… … Физическая энциклопедия

Поиск количественных соотношений структура-свойство — Поиск количественных соотношений структура свойство процедура построения моделей, позволяющих по структурам химических соединений предсказывать их разнообразные свойства. За моделями, позволяющими прогнозировать количественные… … Википедия

QSAR — Поиск количественных соотношений структура свойство процедура построения моделей, позволяющих по структурам химических соединений предсказывать их разнообразные свойства. За моделями, позволяющими прогнозировать количественные… … Википедия

КВАДРАТИЧНАЯ ФОРМА — над коммутативным люльцом с единицей однородный многочлен от n=n(q)переменных с коэффициентами Обычно R это поле С, R или Q, либо кольцо Z, кольцо целых элементов алгебраич. числового поля, а также их пополнения по неархимедовым нормам.… … Математическая энциклопедия

ОБЪЕМ — трехмерного тела числовая характеристика тела, равная в простейшем случае, когда тело можно разбить на конечное множество единичных кубов (т. е. кубов с ребрами длины единица), числу этих кубов. О. трехмерных тел (т. е. множеств трехмерного… … Математическая энциклопедия

Источник

Инварианты подобия и критерии подобия

Если все сходственные величины, определяющие состояние данной системы (натуры) и подобной ей системы (модели), измерять в относительных единицах, т. е. брать сходственное отношение величин для каждой системы, то оно также будет величиной постоянной и безразмерной, например

Можно получить критерии для Любого физического явления. Для этого необходимо иметь аналитическую зависимость между переменными величинами рассматриваемого явления. Критерии подоБия безразмерны (как и инварианты подобия), их значения для каждой точки данной системы могут меняться, но для сходственных точек подобных систем не зависят от относительных размеров натуры и модели.

= 1, или

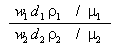
Если отношение констант подобия равно 1, оно носит название Индикатора подобия И указывает на равенство критериев подобия, Следовательно, У подобных явлений индикаторы подобия равны Единице.

Если константы подобия найдены из условий однозначности, то образованные из них критерии называют Определяющими. Критерий, в который входит искомая величина, называют Определяемым. Любая комбинация критериев подобия также представляет собой критерий подобия рассматриваемого явления.

Для некоторой группы подобных процессов критерии подобия имеют определенные численные значения. При переходе к другой группе подобных процессов, описываемых теми же дифференциальными уравнениями, при том же наборе критериев подобия их численные значения будут иными (вследствие, например, различий геометрических характеристик, скоростей потоков и т. д.).

Из сказанного следует, что Любая зависимость между переменными, характеризующими какое-либо явление (т. е. система дифференциальных уравнений), Может быть представлена в виде зависиМости между критериями подобия:

Эту зависимость называют Обобщенным (критериальным) уравнением, А критерии подобия КI — обобщенными переменными величиНами.

Таким образом, теория подобия дает возможность представить решение дифференциальных уравнений и обрабатывать экспериментальные данные в виде обобщенных критериальных уравнений. Это позволяет сократить число экспериментов при получении конкретных уравнений типа (4.1) за счет варьирования критериев подобия, минуя определение всех величин, входящих в критерии подобия уравнения (4.1).

Обычно уравнение (4.1) записывают в виде зависимости определяемого критерия подобия (в который входит искомая величина) от определяющих:

Где К1- определяемый критерий подобия; значения А, п, т Находят опытным путем.

Если какой-либо эффект в исследуемом процессе становится очень слабым по сравнению с другими (численные значения критериев могут быть при этом весьма малы или велики), то его влиянием можно пренебречь. В этом случае критерии, характеризующие интенсивность этого эффекта, могут быть опущены из рассмотрения, и процесс приобретает свойство Автомодельности, Т. е. независимости от этих критериев. Такое моделирование называют Приближенным.

Необходимо иметь в виду, что при использовании теории подобия существуют определенные ограничения. Например, используя методы теории подобия, нельзя получить информации больше, чем ее содержится в исходных уравнениях. Можно без обычных математических методов интегрирования этих уравнений получить их интегральные решения, но если исходные уравнения неверно описывают физическую сущность процесса, то и полученные с использованием методов теории подобия зависимости будут неверны. Кроме того, моделирование на основе метода обобщенных переменных всегда связано с проведением эксперимента, иногда достаточно сложного и большого по объему, требующего значительных затрат времени. Полученные обобщенные уравнения работают надежно только в тех интервалах изменения переменных, которые были использованы при проведении эксперимента.

Источник

Теория подобия

Физическое моделирование

Физическое моделирование проводится на основе экспериментального исследования материальных моделей объекта. При этом возникают три проблемы: какую модель использовать (форма, размер, модельные среды), какие характеристики измерять и как перенести результаты исследований с модели на объект. Эти проблемы разрешаются с помощью теории подобия, являющейся теоретической основой физического моделирования.

Подобные объекты описываются одной системой дифференциальных уравнений и имеют подобные условия однозначности. Подобие условий однозначности включает в себя геометрическое подобие, временное подобие, подобие физических величин, подобие начальных и граничных условий.

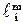
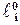
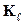
где и— сходственные линейные размеры модели и объекта (длина, диаметр и т.д.), — константа геометрического подобия.

Временное подобие (гомохронность) — постоянство отношения сходственных интервалов времени модели и оригинала.

Если константа временного подобия K_t=1,то такой частный случай гомохромности называют синхронностью, при этом сходственные интервалы времени модели и оригинала совпадают.

Подобие физических величин — постоянство отношения физических величин для модели и оригинала в сходственных точках в сходственные моменты времени

; ;

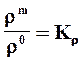
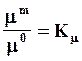
T m /T 0 =K_т – тепловое подобие (подобие полей температуры)

Инварианты подобия еще называют обобщенными, относительными или безразмерными переменными, а также критериями подобия, т.к. они служат признаком, по которому можно судить о подобии модели и оригинала. Инварианты (критерии) подобия подразделяются по различным признакам в зависимости от вида величин, их составляющих на: 1. симплексы и комплексы подобия; 2. определяющие и определяемые критерии; 3. независимые, зависимые и постоянные обобщенные переменные.

Наиболее простой алгоритм получения критериев подобия заключается в следующем: дифференциальное уравнение приводится к безразмерному виду делением всех членов на один из них; все приращения заменяют на абсолютные значения величин; полученные комплексы, количество которых на единицу меньше числа первоначальных членов уравнения, являются критериями подобия.

В качестве примера рассмотрим получение критерия Ньютона из одноименного уравнения

; ; (73)

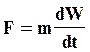
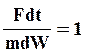
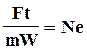
Рассмотрим без доказательства три теоремы подобия.

1.Подобные объекты характеризуются численно равными критериями подобия (Ньютон, Бертран).

2.Решение дифференциального уравнения (системы уравнений), описывающего объект, может быть представлено в виде зависимости между критериями подобия (Бэкингем, Федерман, Афанасьева-Эренфест).

(74)

(75)

(76)

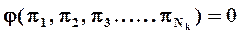
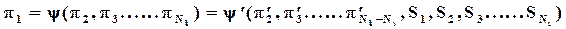
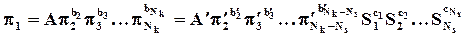
Таким образом, теория подобия позволяет обобщать результаты эксперимента и распространять их на широкий класс подобных явлений.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Инварианты и критерии подобия

Инварианты и критерии подобия

При прямом обратимом процессе производится работа, достаточная для возвращения системы при тех же внешних условиях в первоначальное состояние. Людмила Фирмаль

В результате прямого и обратного обратимых процессов в системе и во внешней среде не происходит каких-либо остаточных конечных изменений. Людмила Фирмаль

По n он указывает нормальное расстояние между 2 изотермами. Это характерное значение теплопроводности process. In в процессе теплопередачи эта величина составляет не только n, поэтому, чтобы сделать полученный результат более общим, необходимо заменить n на, что является размерной характеристикой конкретной задачи. Подобные найденные условия принимают вид — у k1et. 12. 6 Вы можете получить тот же результат, используя инварианты подобия. Безразмерный комплекс вида 12. 6, состоящий из физических величин, характерных для данного явления, называется коррекцией и подобием. Критерию присваивается имя выдающегося ученого, обозначенное первыми 2 буквами выбранного имени.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Подобными называют явления, для которых постоянны отношения характеризующих их сходственных величин.

Условия подобия рассмотрим первоначально на простейшем примере геометрического подобия. Как известно из геометрии, из класса однородных плоских фигур (треугольников, многоугольников и др.) можно выделить группы подобных фигур, например треугольников, сходственные линейные размеры которых параллельны, а отношения этих размеров постоянны. Подобные фигуры отличаются друг от друга только масштабом и могут быть получены одна из другой умножением сходственных размеров одной из них на некоторый постоянный масштабный множитель.

Безразмерные масштабные множители, выражающие отношения однородных сходственных величин подобных фигур (или любых подобных систем), называются константами подобия. Например, если размеры сторон одного треугольника равны а’, b’ и с’, а размеры сходственных сторон подобного ему треугольника составляют а», b» и с», то

где 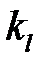– константа геометрического подобия (индекс указывает на подобие линейных размеров).

Подобие может быть охарактеризовано также инвариантами подобия, которыми, в отличие от констант подобия, выражающих отношения сходственных величин разных фигур, называют безразмерные отношения каких-либо двух размеров, одной из фигур, равные отношению сходственных размеров подобной фигуры. Так, для рассматриваемых подобных треугольников

где 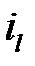– инвариант геометрического подобия.

Инварианты подобия представляют собой выражения величин в относительных единицах, т. е. в безразмерном виде. Например, в данном случае одна из сторон (а) подобных треугольников выражена в относительных единицах, причем в качестве масштаба для ее измерения выбрана их другая сторона (b). В тех же единицах, очевидно, можно выразить также третью сторону (с) подобных треугольников.

Для подобия физических явлений соблюдение геометрического подобия систем (аппаратов), в которых они протекают, является необходимым, но не достаточным условием. При подобии физических процессов должны быть подобны все основные физические величины, влияющие на процесс.Эти величины изменяются по мере протекания процесса (во времени) и в различных точках аппарата, т.е. в пространстве. Поэтому технологические процессы подобны только при условии совместного соблюдения геометрического и временного подобия, подобия полей физических величин, а также подобия начальных и граничных условий.

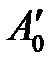
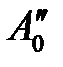
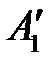
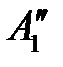
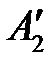
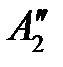
Сформулируем эти условия на примере подобного движения вязкой жидкости в натуре (в производственном трубопроводе) и в ее уменьшенной модели (рис. 7-1). Для этого рассмотрим любые сходственные точки, лежащие, например, на оси труб: и (на входе), а также и , и и т. д.

Геометрическое подобие соблюдается при равенстве отношений всех сходственных линейных размеров натуры и модели:

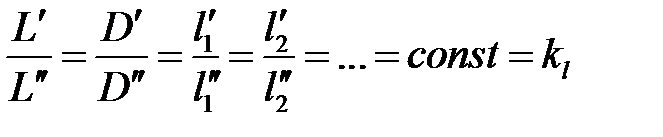7-1

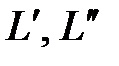
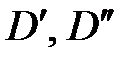
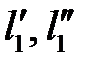
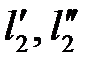
где – длина натуры и модели; – диаметр натуры и модели; и и т. д. –пути, проходимые сходственными частицами жидкости от входа до произвольной точки, сходственной для натуры и модели.

При подобном движении сходственных частиц их траектории в натуре и в модели также должны быть подобны. Это условие иногда называют кинематическим подобием.

Постоянная величина 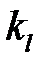характеризующая соотношение между геометрическими параметрами подобных систем и позволяющая перейти от размеров одной системы к размерам другой, представляет собой, как указывалось, константу геометрического подобия.

Временное подобие характеризуется тем, что сходственные частицы в геометрически подобных системах, двигаясь по геометрически подобным траекториям, проходят геометрически подобные пути за промежутки времени, отношение которых является постоянной величиной, т. е.

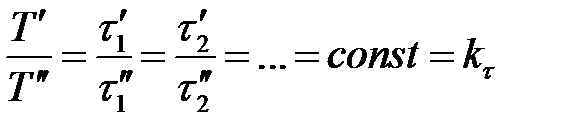7-2

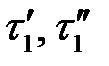
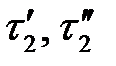
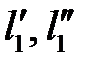
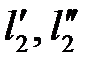
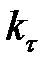
где Т’, Т» – время прохождения сходственными частицами всего трубопровода (натуры и модели соответственно); , и т. д. –время прохождения сходственными частицами подобных путей , и т. д.; – константа временного подобия.

При соблюдении геометрического и временного подобия будет соблюдаться также подобие скоростей

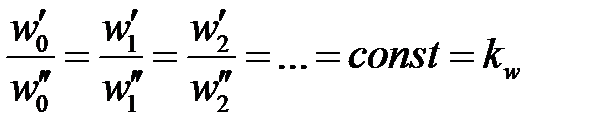7-3

Подобие физических величин предполагает, что для двух любых сходственных точек натуры и модели, размещенных подобно в пространстве и времени (т. е. при соблюдении геометрического и временного подобия), отношения физических свойств являются величинами постоянными. Так, например, если движущиеся по трубопроводам жидкости имеют вязкость, плотность и т.д., то для сходственных точек натуры и модели

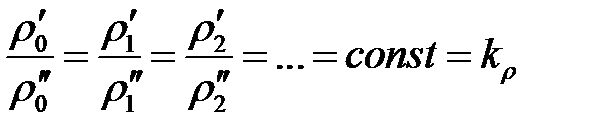7-4

Подобие начальных и граничных условий предполагает, что отношения основных параметров в начале и на границе натуры и модели являются соответственно величинами постоянными. Иными словами, для начальных и граничных условий должно соблюдаться геометрическое, временное и физическое подобие, как и для других сходственных точек натуры и модели.

Константы подобия 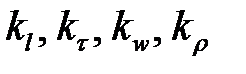и т.д., выражающие отношения различных одноименных величин в натуре и в модели, постоянны для различных сходственных точек подобных систем, но изменяются в зависимости от соотношения размеров натуры и модели.

Отметим еще одно важное свойство констант подобия: входящие в них одноименные величины могут взаимно заменяться. Поэтому отношения приращений этих величин можно заменять отношениями самих величин. Например:

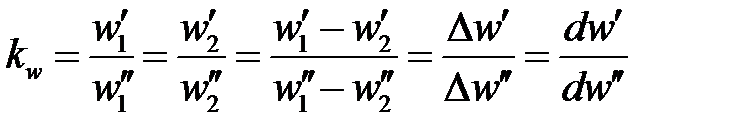7-5

Подобие потоков в натуре и модели можно охарактеризовать также с помощью инвариантов подобия, выражая все подобные величины в относительных единицах, т. е. в виде отношений сходственных величин в пределах каждой системы. Так, из уравнения (7-1) следует:

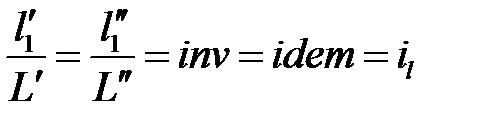7-6

причем 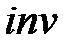, или , – означает инвариантно, или «одно и то же».

Величина 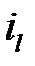представляет собой инвариант подобия геометрических величин.

При выражении любой величины в относительных единицах в качестве масштаба ее измерения может быть выбрано значение этой величины в любой точке системы. Например, в выражении (7-6) за масштаб вместо длины труб L’ и L» можно принять их диаметры и т. д.

Аналогично и для других подобий

Приведенные выше инварианты подобия, выраженные отношением двух однородных физических величин (параметров), называются параметрическими критериями, или симплексами.

Однако инварианты подобия могут быть выражены также отношениями разнородных величин, т. е. представлять собой безразмерные комплексы этих величин. Например, как показано ниже, для сходственных точек подобных потоков в трубопроводах равны инварианты подобия, состоящие из различных физических величин, или безразмерные комплексы, являющиеся уже известным нам критерием Рейнольдса:

Если инварианты подобия выражаются комплексами величин, полученными преобразованием дифференциальных уравнений, описывающих процесс, то их называют критериями подобия. Критерии подобия всегда имеют физический смысл, являясь мерами соотношения между какими-то двумя эффектами (силами и т. п.), существенными для рассматриваемого процесса.

Критерии подобия обладают всеми свойствами инвариантов: они безразмерны, могут изменять свое значение от точки к точке данной системы, но для сходственных точек подобных систем не зависят от относительных размеров натуры и модели. В силу безразмерности числовые значения критериев подобия, как и констант и инвариантов подобия, не зависят от применяемой системы единиц.

Критерии подобия могут быть получены для любого процесса, если известны аналитические зависимости между характеризующими его величинами – дифференциальные уравнения, описывающие процесс. Вместе с тем следует отметить, что один и тот же процесс, которому соответствует определенное дифференциальное уравнение, может быть интегрально описан при использовании различных систем критериев.

Безразмерные симплексы или комплексы величин, в частности критерии подобия, называют также обобщенными переменными.

Основные положения теории подобия обобщаются теоремами подобия. Эти теоремы лежат в основе практического применения теории подобия.

Источник