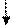Что называется эпюром монжа комплексным чертежом и как он образуется

Чертежик

Метки

эпюра монжа или комплексный чертеж

Эпюра монжа или комплексный чертеж — это чертеж, составленный из двух или более связанных между собой ортогональных проекций геометрической фигуры.

Пользоваться пространственным макетом для отображения ортогональных проекций геометрических фигур неудобно ввиду его громоздкости, а также из-за того, что при его переносе на лист бумаги, на плоскостях H и W происходит искажение формы и размеров проецируемой фигуры.
Поэтому вместо изображения на чертеже пространственного макета используется эпюра Монжа.

Эпюра Монжа получается преобразованием пространственного макета путем совмещения плоскостей H и W с фронтальной плоскостью проекций V:
— для совмещения плоскости H с V поворачиваем ее на 90 градусов вокруг оси x в направлении движения часовой стрелки. На рисунке, для наглядности, плоскость H повернута на угол чуть меньший 90 градусов, при этом ось y, принадлежащая горизонтальной плоскости проекции, после поворота совпадает с осью z;
— после совмещения горизонтальной плоскости, поворачиваем вокруг оси z также на угол 90 градусов профильную плоскость в направлении противоположном движению часовой стрелки. При этом ось y, принадлежащая профильной плоскости проекции, после поворота совпадает с осью x.

Так как плоскости не имеют границ, то в совмещенном положении (на эпюре) эти границы не показывают, нет необходимости оставлять надписи, указывающие положение пол плоскостей проекций. Излишне также напоминать, где отрицательное направление координатных осей. Тогда, в окончательном виде эпюра Монжа, заменяющая чертеж пространственного макета примет вид, показанный на рисунке.

— обычных чертежных инструментов и приспособлений:
Чертежные инструменты;
Чертежные принадлежности и приборы;
— Программы для построения (рисования) эпюра Монжа: Выполнение чертежа в графическом редакторе.

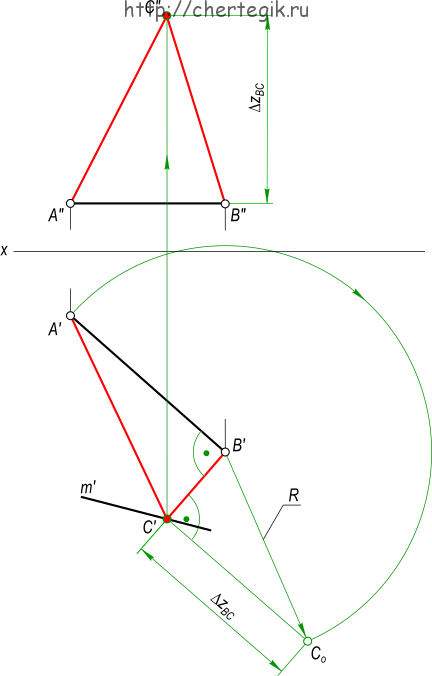
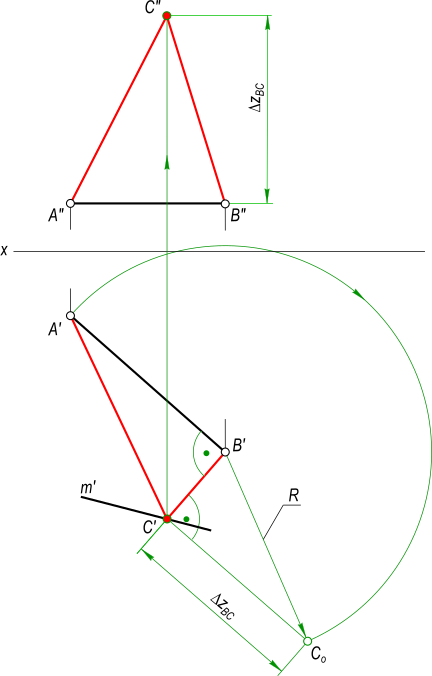
В качестве примера оформления эпюра Монжа предлагаем решение задачи на построение равнобедренного прямоугольного треугольника ABC:

— в черном цвете отображается известное по условию задачи;
— в зеленом цвете отображаются все построения которые ведут к решению задачи;
— в красном цвете отображается найденные искомые задачи.
По условию задачи заданы проекции треугольника ABC(A`B`C`, A»B»…»). Для решения задачи необходимо найти недостающую проекцию C».

Источник

Лекция 2. Комплексный чертеж точки (Эпюр Монжа)

Комплексный чертеж точки (Эпюр Монжа)

ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ

Проецирование геометрического объекта (точки, линии или фигуры) на одну плоскость проекций не определяет его положения в пространстве (какой-либо проекции точки может соответствовать бесчисленное множество точек в пространстве) и не дает полного представления о нем. Поэтому принято использовать не одну, а две или три взаимно перпендикулярные плоскости проекций – горизонтальную , фронтальную и профильную . Две плоскости проекций делят пространство на 4 четверти (рис. 2.1 а), три плоскости – на 8 октантов (рис. 2.1 б).

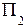
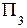
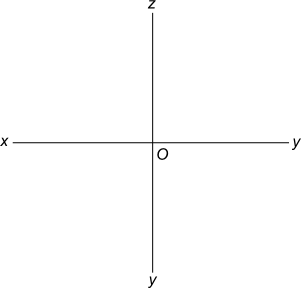
Линии пересечения плоскостей проекций 0x, 0y, 0z называются осями проекций. Они аналогичны осям декартовой системы координат с той разницей, что ось 0x имеет положительное направление влево.

Т.к. любой предмет можно рассматривать как множество точек, проецирование его на плоскость сводится к построению отдельных точек ему принадлежащих. Поэтому все базовые понятия и правила проецирования рассматриваются на примере построения точки.

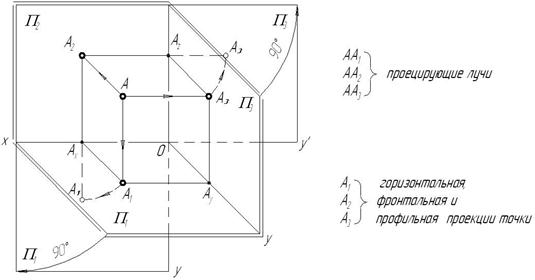
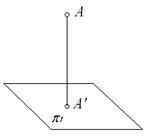
Построим проекции точки А, расположенной в первом октанте пространства (рис.2.2). Для этого через точку проведем проецирующие лучи, идущие перпендикулярно плоскостям проекций. На пересечении этих лучей с плоскостями проекций находятся проекции самой точки А.

Несмотря на наглядность пространственного изображения, работать с ним неудобно, т.к. горизонтальная и профильная плоскости проекций изображаются на нем с искажением. Удобнее совместить эти плоскости с фронтальной плоскостью проекций, развернув их на угол 90° вокруг осей проекций 0x и 0y. При этом ось 0y разворачивается как с горизонтальной, так и с фронтальной плоскостями проекций, поэтому на чертеже она обозначается дважды – 0y и 0y′.

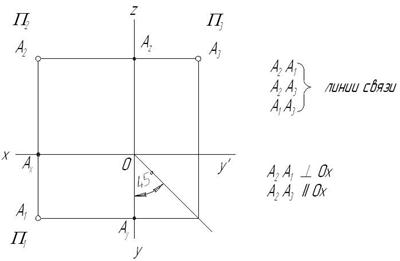
Полученный таким образом чертеж называется комплексным чертежом (КЧ), или эпюром Монжа. В связи с тем, что он представляет собой развернутую в плоскость пространственную модель, самой точки на комплексном чертеже нет (рис. 2.3).

Проекции точки на КЧ соединяются между собой пря­мыми линиями, называющимися линиями связи и проходящими перпендикулярно осям проекций.

Независимо от того, в каком октанте находится точка, ее горизонтальная и фронтальная проекции всегда лежат на одной линии связи, перпендикулярной оси 0x, а фронтальная и профильная проекция – на линии связи, перпендикулярной оси 0z.

Исходя из рисунка пространственной модели (рис. 2.2) можно выявить взаимосвязь между проекциями точки А:

1) расстояние от точки А до горизонтальной плоскости проекций (высота точки)

;

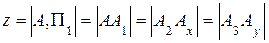
2) расстояние от точки А до фронтальной плоскости проекций (глубина точки)

;

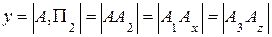
3) расстояние от точки А до профильной плоскости проекций (широта точки)

.

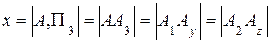
Например, расстояние от фронтальной проекции точки до оси 0x равно расстоянию от профильной проекции до оси 0y. Следовательно, по двум любым проекциям точки можно построить третью.

Точки могут занимать частное положение в пространстве относительно плоскостей проекций:

1) если точка расположена на оси проекций, то две ее проекции лежат на этой оси, а третья находится в начале координат;

2) если точка лежит на плоскости проекций, тогда одна из ее проекций лежит в этой плоскости, а две другие – на осях проекций.

Допустим, что точка В лежит на оси 0z, а точка С принадлежит горизонтальной плоскости проекций (рис. 2.4). Для точки С построения следует начинать с проекции, принадлежащей плоскости , для точки В – с проекций и , лежащих на осях проекций.

Источник

Научная электронная библиотека

Пиралова О. Ф., Ведякин Ф Ф.,

1.5. Система трех плоскостей проекций. Эпюр монжа

Все пространственные геометрические фигуры могут быть ориентированы относительно декартовой прямоугольной системы координатных осей – системы трех взаимно перпендикулярных координатных плоскостей (рис. 1.12).

Эти координатные плоскости обозначаются:

1. Горизонтальная плоскость проекций – π1;

2. Фронтальная плоскость проекций – π2;

3. Профильная плоскость проекций – π3.

Рис. 1.12. Изображение системы трех плоскостей проекций

Линии пересечения этих плоскостей образуют координатные оси: ось абсцисс – Х; ось ординат – Y; ось аппликат – Z. Точка пересечения координатных осей принимается за начало координат и обозначается буквой О.

Положительными направлениями осей считают: для оси x – влево от начала координат, для оси Y – в сторону зрителя от плоскости π2, для оси z – вверх от плоскости π1; противоположные направления считают отрицательными.

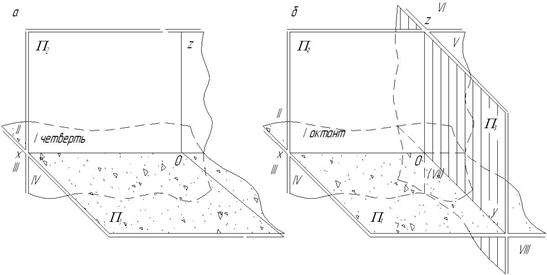
Для упрощения дальнейших рассуждений будем рассматривать только часть пространства, расположенную влево от профильной плоскости проекций π3.

При таком допущении три координатные плоскости проекций образуют четыре пространственных угла – октанта (в общем случае – 8 октантов).

Каждый из октантов представляет часть пространства, в котором располагаются геометрические элементы (точки, прямые, плоскости и поверхности), определяемые соответствующими размерами. Положение этих элементов в пространстве определяется координатами в выбранной системе. Система трёхмерная, поэтому каждая точка пространства имеет три координаты – х,у,z.

Координатой считается кратчайшее расстояние от точки до соответствующей плоскости проекций.

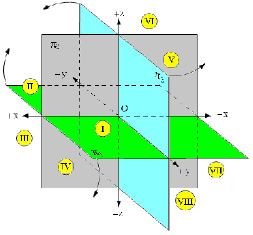
Оси ординат Y и аппликат Z делят профильную плоскость проекций π3 на четыре части:

1. Верхнюю переднюю полу π3 (оси Y и Z)

Для того, чтобы получить плоскую (двухмерную) модель пространственных координатных плоскостей проекций, горизонтальную π1 и профильную π3 плоскости совмещают с фронтальной π2 в том порядке как это показано стрелками на рис. 1.12.

При этом горизонтальная плоскость проекций π1 вращается вокруг оси Х на 90°, а профильная плоскость проекций π3 вращается вокруг оси Z также на 90° (направление вращения показано на рис. 1.12).

Полученное таким образом совмещение трех плоскостей проекций (рис. 1.13) является плоской моделью системы трех пространственных координатных плоскостей.

Для построения плоской модели пространственной геометрической фигуры каждая ее точка проецируется ортогонально на плоскости проекций π1, π2 и π3, которые затем совмещаются в одну плоскость. Полученная таким образом плоская модель пространственной геометрической фигуры называется эпюром[2] Монжа или комплексным чертежом Монжа [1,2,5].

Обычно, такая модель даёт три проекции: фронтальную, горизонтальную и профильную.

Порядок построения эпюра точки,
расположенной в первом октанте.

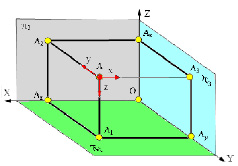
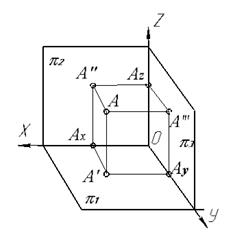
На рис. 1.13 изображена пространственная точка А, координаты которой (x, y, z) показывают величины расстояний, на которые точка удалена от плоскостей проекций.

Рис. 1.13. Пространственная модель точки А

Для того чтобы получить ортогональные проекции точки А, необходимо из этой точки опустить перпендикуляры на плоскости проекций.

Точки пересечения этих перпендикуляров с плоскостями проекций образуют проекции точки А:

А1 – горизонтальную проекцию точки;

А2 – фронтальную проекцию точки;

А3 – профильную проекцию точки.

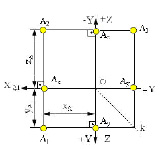
На рис. 1.14 плоскости проекций π1 и π3 совмещены с плоскостью чертежа (с плоскостью проекции π2), а вместе с ними совмещены с плоскостью чертежа и проекции точки А (А1, А2, А3) и, таким образом, получена плоскостная модель координатных плоскостей проекций и плоскостная модель пространственной точки А – её эпюр. Положение проекций точки А на эпюре однозначно определяется ее тремя координатами (рис. 1.14).

На рис. 1.13 и рис. 1.14 также видно, что на эпюре горизонтальная и фронтальная проекции точки лежат на одном перпендикуляре к оси Х, а также фронтальная и профильная проекции – на одном перпендикуляре к оси Z:

Рис. 1.14. Эпюр точки А

Из рис. 1.12 видно, что точки, расположенные в различных октантах, имеют определенные знаки координат.

В таблице приведены знаки координат точек, расположенных в различных октантах.

Источник

Эпюра Монжа

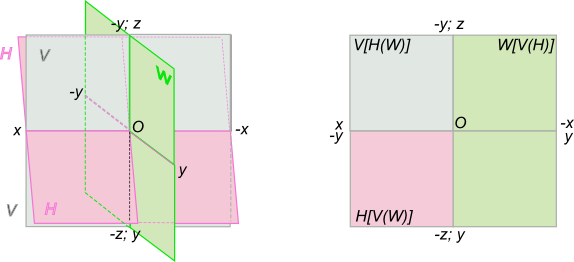
Пользоваться пространственным макетом для отображения ортогональных проекций геометрических фигур неудобно ввиду его громоздкости, а также из-за того, что при его переносе на лист бумаги, на плоскостях H и W происходит искажение формы и размеров проецируемой фигуры. Поэтому вместо изображения на чертеже пространственного макета используется эпюра Монжа.

После преобразования пространственный макет примет вид, показанный на рисунке. На этом рисунке указана также последовательность взаимного положения пол плоскостей проекций, так запись V[H(W)] указывает, что в этой части эпюра Монжа (ограниченного положительным направлением осей x и z) ближе к нам находится верхняя левая пола фронтальной плоскости проекции V, за ней располагается задняя левая пола горизонтальной плоскости проекции H, далее следует верхняя задняя пола профильной плоскости W.

Так как плоскости не имеют границ, то в совмещенном положении (на эпюре) эти границы не показывают, нет необходимости оставлять надписи, указывающие положение пол плоскостей проекций. Излишне также напоминать, где отрицательное направление координатных осей. Тогда, в окончательном виде эпюра Монжа, заменяющая чертеж пространственного макета примет вид, показанный на рисунке.

В качестве примера оформления эпюра Монжа предлагаем решение задачи на построение равнобедренного прямоугольного треугольника ABC:

Источник

Комплексный чертеж точки или эпюр Монжа.

Лекция

По дисциплине «Инженерная графика»

Раздел. 1 Начертательная геометрия

Введение.

Начертательную геометрию называют также теорией изображений. Предметом начертательной геометрии является изложение и обоснование способов изображения пространственных фигур на плоском чертеже и способов решения пространственных геометрических задач на плоском чертеже.Стереометрические (трехмерные) объекты обсуждаются в ней с помощью планиметрических (двухмерных) изображений этих объектов, проекций.

Говорят, что чертеж – язык техники, а начертательная геометрия – грамматика этого языка. Начертательная геометрия является теоретической основой построения технических чертежей, которые представляют собой полные графические модели конкретных инженерных изделий.

Правила построения изображений, излагаемых в начертательной геометрии, основаны на методе проекций.

Изучение начертательной геометрии способствует развитию пространственного представления и воображения, конструктивно геометрического мышления, развитию способностей к анализу и синтезу пространственных форм и отношений между ними. Освоению способов конструирования различных геометрических пространственных объектов, способов получения их чертежей на уровне графических моделей и умению решать на этих чертежах задачи, связанные с пространственными объектами и их геометрическими характеристиками.

Основание начертательной геометрии как науке было положено французским ученым и инженером Гаспаром Монжем (1746-1818) в его труде “Начертательная геометрия”, Париж, 1795 г. Гаспар Монж дал общий метод решения стереометрических задач геометрическими построениями на плоскости, то есть на чертеже, с помощью чертежных инструментов.

p₁ – горизонтальная плоскость проекций,

p₂ – фронтальная плоскость проекций,

, , — плоскости

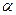
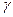
Проекции точек, прямых, плоскостей обозначаются: на p₁ с одним штрихом, на p₂ с двумя, на p₃ – с тремя штрихами.

1 Центральное проецирование.

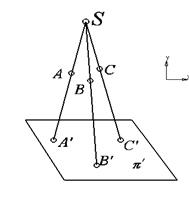
Аппарат центрального проецирования состоит из центра проецирования S, плоскости проекций π, проецирующих лучей.

S – центр проецирования

Проекция – это точка пересечения проецирующего луча с плоскостью проекций.

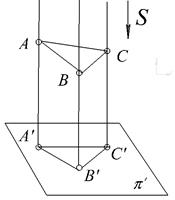
2. Параллельное проецирование.

Проецирующие лучи проводятся параллельно S и друг другу. Параллельные проекции делятся на косоугольные и прямоугольные. При косоугольном проецировании лучи расположены под углом к проецирующей плоскости.

При прямоугольном проецировании проецирующие лучи перпендикулярны плоскости проекций (рис. 1.3). Прямоугольное проецирование является основным способом проецирования, принятым при построении технических чертежей

Основные свойства ортогонального проецирования

2. Проекция прямой (в общем случае) – есть прямая линия или точка(прямая перпендикулярна плоскости проекций);

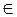
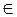
3. Если точка лежит на прямой, то проекция этой точки будет принадлежать проекции прямой: А l ® A’ l’;

4. Если две прямые в пространстве параллельны, то их одноименные проекции также параллельны: a || b ® a` || b`;

5. Если две прямые пересекаются в некоторой точке, то их одноименные проекции пересекаются в соответствующей проекции этой точки: m ∩ n = K ® m’ ∩ n’ = K’;

6. Пропорциональность отрезков, лежащих на одной прямой или на двух параллельных прямых, сохраняется и на их проекциях (рис.1.3): АВ:СD = А’B’: C’D’

7. Если одна из двух взаимно перпендикулярных прямых параллельна плоскости проекций, то прямой угол проецируется на эту плоскость прямым углом (рис.1.4).

Комплексный чертеж точки или эпюр Монжа.

Самый употребительный на практике метод начертательной геометрии предложил Гаспар Монж. В основе этого метода лежит ортогональное проектирование.

Ортогональной (или прямоугольной) проекцией точки А на плоскость π₁ называют основанием перпендикуляра, опущенного из точки А на плоскость π₁ (рис.1.5)

Получаемый при этом на плоскости π₁ чертеж необратим, соответствие между оригиналом А и проекцией A’ однозначно только в одну сторону: от оригинала к проекции. Оригиналу соответствует единственная проекция, оригиналом чертеж определен однозначно, но для проекции A’ существует бесчисленное множество соответствующих ей оригиналов, а именно все точки проецирующей прямой A A’. Точный перевод с языка чертежа на язык натуры невозможен. Поэтому Монж вводит вторую плоскость проекций.

На рис. 6. изображена прямоугольная система координат.

Совмещая теперь плоскости π₁ и π₂ с построенными в них проекциями поворотом π₁ вокруг оси Х на 90 0 так, чтобы передняя полуплоскость π₁ совпала с нижней полуплоскостью π₂, получаем комплексный чертеж точки или эпюр Монжа. (рис. 1.7).

Построенный по таким правилам чертеж, состоящий из пары проекций, расположенных в проекционной связи, обратим, то есть соответствие между оригиналом и чертежом однозначно в обе стороны. Или иначе говоря, чертеж дает исчерпывающую информацию об оригинале. Расшифровка этой информации и составляет предмет начертательной геометрии.

Из комплексного чертежа точки можно сделать выводы:

1. две проекции точки вполне определяют положение точки в пространстве;

2. проекции точек всегда лежат на линии связи, перпендикулярной оси проекции.

A’ A» Х

Линии, соединяющие проекции точек, называются линиями связи и изображаются сплошными тонкими линиями.

Чтобы получить комплексный чертеж точки необходимо расположить три плоскости в одной, для чего «разрезаем» ось У и совмещаем три основные плоскости проекций в одну (рис.1. 9).

Новой информации об оригинале третья проекция не добавляет. Она лишь делает имеющуюся информацию более удобоваримой. (Рис. 1.10)

Расстояние от точки А до плоскости π₃ (А A»‘) в пространстве можно увидеть на чертеже и оно равно расстоянию A’AY = A»A_Z = A_X0 = X

Расстояние от точки А до плоскости π₂ (А A») в пространстве можно увидеть на чертеже и оно равно расстоянию A’AX = A»‘A_Z = A_Y0 = Y

Расстояние от точки А до плоскости π₁ (А A’) в пространстве можно увидеть на чертеже и оно равно расстоянию A»AX = A»‘A_Y = A_Z0 = Z

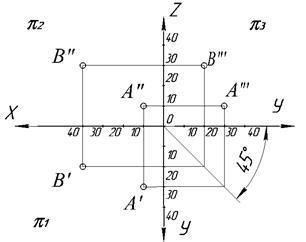
Пример. Построить проекции точек А(10, 10,30), В(30,20,10)

Точки, у которых совпадает одна пара одноименных проекций (а другие не совпадают), называются конкурирующими точками.

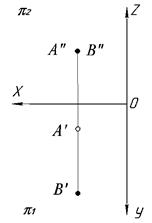
Точки расположены на одной проецирующей прямой, перпендикулярной фронтальной плоскости проекций. Направление взгляда указано стрелкой. При этом проекция B’ ближе к наблюдателю, чем A’, и на π₂ видимой будет проекция B» а проекция А» будет невидимой (рис. 1.12).

Точки расположены на одной проецирующей прямой, перпендикулярной горизонтальной плоскости проекций. Направление взгляда указано стрелкой. При этом проекция А» ближе к наблюдателю, чем В», и на π₁ видимой будет проекция А’ а проекция В’ будет невидимой (рис. 1.13).

Чем дальше проекция точки от оси Х, тем точка выше или ближе к наблюдателю.

Источник