Что называется четной функцией
Четная функция
Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.
Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.
Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.
Содержание
Определения
Свойства
Примеры
Нечётные функции
Чётные функции
Вариации и обобщения
Полезное
Смотреть что такое «Четная функция» в других словарях:
ЧЕТНАЯ ФУНКЦИЯ — функция, удовлетворяющая равенству f( x) = f(x) при всех x … Большой Энциклопедический словарь
ЧЕТНАЯ ФУНКЦИЯ — функция, не меняющая знак при изменении знака независимого переменного, т. е. функция, удовлетворяющая условию f( x)=f(x). График Ч. ф. симметричен относительно оси ординат … Математическая энциклопедия
ЧЕТНАЯ ФУНКЦИЯ — функция, удовлетворяющая равенству f( x) = f(x) при всех х … Естествознание. Энциклопедический словарь
чётная функция — функция, удовлетворяющая равенству f( х) = f(х) при всех х. * * * ЧЕТНАЯ ФУНКЦИЯ ЧЕТНАЯ ФУНКЦИЯ, функция, удовлетворяющая равенству f( x) = f(x) при всех x … Энциклопедический словарь
Многочлены Лежандра — Многочлен Лежандра многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов, на отрезке по мере Лебега. Многочлены Лежандра могут быть получены из многочленов… … Википедия
Спектральная плотность — В статистической радиотехнике и физике при изучении детерминированных сигналов и случайных процессов широко используется их спектральное представление в виде спектральной плотности, которая базируется на преобразовании Фурье. Если процесс имеет… … Википедия
ЛЮКСЕМБУРГА НОРМА — функция где М(и) четная выпуклая функция, возрастающая при положительных U, М(u)>0 при u>0, G ограниченное замкнутое множество в Свойства этой нормы были изучены В. Люксембургом [1]. Л. н. эквивалентна норме Ор лича (см. Орлича… … Математическая энциклопедия
ВЕИЕРШТРАССА ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ — ф>тнкции, положенные К. Вейерштрассом в основу его общей теории эллиптических функций, излагавшейся им с 1862 на лекциях в Берлинском университете (см. [1], [2]). В отличие от более раннего построения теории эллиптич. функций, связанного с… … Математическая энциклопедия
Четные и нечетные функции
Функция называется четной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство
График четной функции симметричен относительно оси ординат.
Например, — четные функции.
Функция называется нечетной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство
График нечетной функции симметричен относительно начала координат.
Например, — нечетные функции.
Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида.
Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задания:
1. Проверьте, является ли функция четной (нечетной).
Область определения функции
Проверим, является ли чётной или нечётной. Если функция четна. Если функция нечетна.
— значит, функция нечётная, её график симметричен относительно нуля.
2. Проверьте, является ли функция четной (нечетной)
Область определения: все действительные числа.
— чётная, как сумма двух чётных функций.
Её график симметричен относительно оси y.
3. Проверьте, является ли функция четной (нечетной).
Область определения функции симметрична относительно нуля.
— чётная, её график симметричен относительно оси y.
Четные и нечетные функции
Вы будете перенаправлены на Автор24
Четные функции
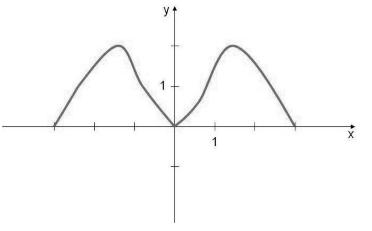
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будет совпадать, то график этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).
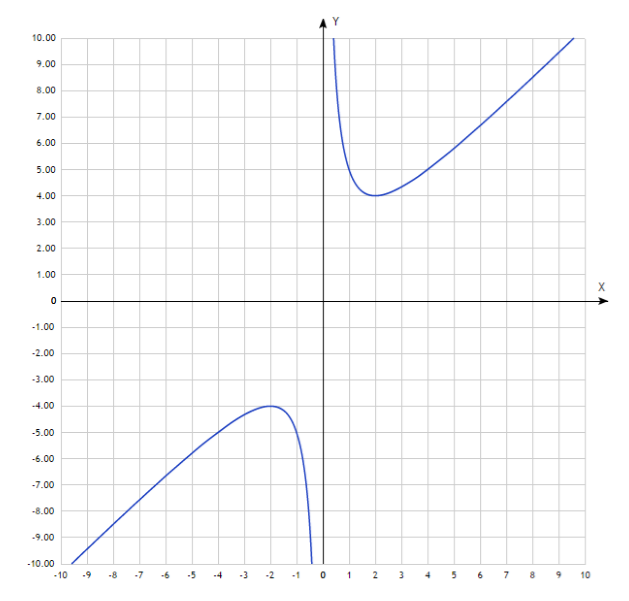
Нечетные функции
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будут также совпадать по модулю и отрицательны по знакам, то график этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).
Готовые работы на аналогичную тему
Функция общего вида
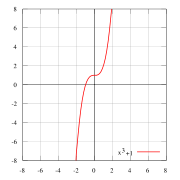
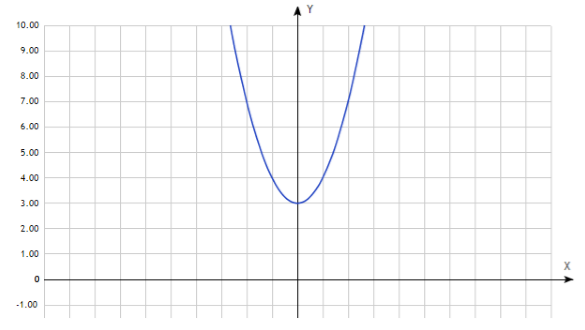
Функция общего вида никогда не будет симметрична оси ординат и началу координат. Пример функции общего вида изображен на рисунке 3.
Пример задачи
Исследовать функцию на четность и нечетность и построить их графики.
Изобразим её на графике:
Изобразим её на графике:
Изобразим её на графике:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 04 07 2021
Четные и нечетные функции
Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.
Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.
Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.
Содержание
Определения
Свойства
Примеры
Нечётные функции
Чётные функции
Вариации и обобщения
Полезное
Смотреть что такое «Четные и нечетные функции» в других словарях:
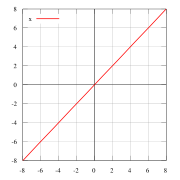
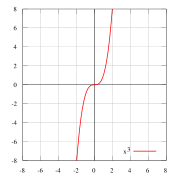
Нечетные и четные функции — f(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия
Земляков — Земляков, Александр Николаевич Файл:Zemlyakov.jpg Александр Николаевич Земляков (17 апреля 1950(19500417), Бологое 1 января 2005, Черноголовка) математик,выдающийся советский и российский педагог, автор учебно педагогической… … Википедия
Земляков, Александр Николаевич — Александр Николаевич Земляков (17 апреля 1950(19500417), Бологое 1 января 2005, Черноголовка) математик, выдающийся советский и российский педагог, автор учебно педагогической литературы. Биография Закончил в 1967 году с золотой… … Википедия
Ряд Фурье — Добавление членов ряда Фурье … Википедия
H.265 — или HEVC (англ. High Efficiency Video Coding высокоэффективное видеокодирование) предполагаемая будущая рекомендация ITU T и проект стандарта ISO/IEC по сжатию видео с применением более эффективных алгоритмов по сравнению с H.264/MPEG… … Википедия
МАРЦИАН КАПЕЛЛА — МАРЦИАН КАПЕЛЛА (Martianus Minneius Felix Capeila) (2 я пол. 5 в. н. э.), латинский платоник, последний латинский выразитель «религии культуры» спасения через пайдейю. Известен как автор сочинения «О браке Филологии и Меркурия» (De nuptiis… … Античная философия
Link 16 — (TADIL J) тип военной тактической сети обмена данных, близкому к реальному. Используется США и странами НАТО. Является одной из составных частей семейства тактических сетей передачи данных TADIL (англ. Tactical Digital Information Link … Википедия
ЛАНДАУ ТЕОРЕМЫ — теоремы для регулярных в круге функций, устанавливающие нек рые связи между геометрич. свойствами производимого этими функциями конформного отображения и начальными коэффициентами представляющих их степенных рядов. В 1904 Э. Ландау показал [1],… … Математическая энциклопедия
Четность и нечетность функции. Период функции. Экстремумы функции
Содержание
Способы задания функции
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Четная и нечетная функция
Функция является ни четной, ни нечетной и называется функцией общего вида, когда она не обладает симметрией относительно оси или начала координат.
Исследуем на четность нижеприведенную функцию:
Значит, функция f(x)=3x^<3>-7x^ <7>является нечетной.
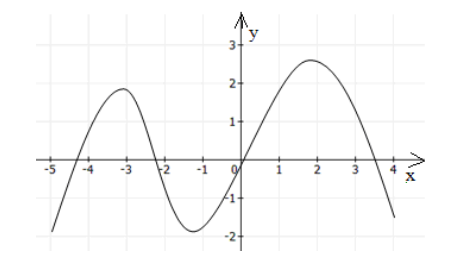
Периодическая функция
f(x) > 0 на (x_<1>; x_<2>) \cup (x_<3>; +\infty )
f(x) на (-\infty; x_ <1>) \cup (x_<2>; x_ <3>)
Ограниченность функции
Возрастающая и убывающая функция
Корнями функции принято называть точки, в которых функция F=y(x) пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0 ).
а) Если при x > 0 четная функция возрастает, то убывает она при x
б) Когда при x > 0 четная функция убывает, то возрастает она при x
в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x



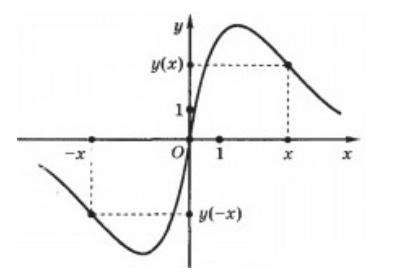




.png)

.png)