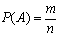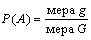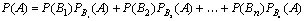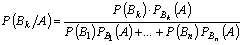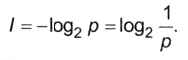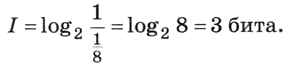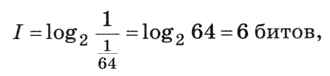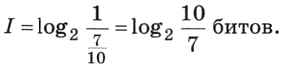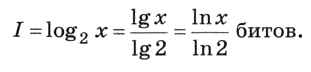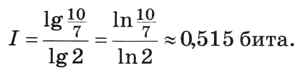Что можно сказать о вероятностях событий входящих в полную систему информатика

Тема 8. СОБЫТИЕ И ВЕРОЯТНОСТЬ

8.1. Понятие о случайном событии

Наблюдение явления, опыт, эксперимент, которые можно провести многократно, в теории вероятностей принято называть испытанием. Примеры: сдача экзамена, наблюдение за дорожно-транспортными происшествиями, выстрел из винтовки, бросание игрального кубика, педагогический эксперимент.

Результат, исход испытания называется событием. Примеры: успешная сдача экзамена, дорожно-транспортные происшествия со смертельным исходом, попадание в цель, появление того или иного числа очков на брошенной игральной кости, получение результата при проведении педагогического эксперимента.

Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании. Примеры: совместные события: идет дождь и идет снег, человек ест и человек читает, число целое и четное; несовместные события: день и ночь, человек читает и человек спит, число иррациональное и четное.

Два события называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит. Примеры: если сейчас день, то сейчас не ночь; если человек спит, то в данный момент он не читает; если число иррациональное, то оно не является четным.

Событие называется достоверным, если в данном испытании оно является единственно возможным его исходом. Событие называется невозможным, если в данном испытании оно заведомо не может произойти. Примеры: если в урне все шары белые, то достать белый шар является достоверным событием, а достать черный шар является невозможным событием; если человек прыгнул в воду, то выйти мокрым является достоверным событием, а выйти сухим является невозможным событием.

Событие называется случайным, если его наступление или ненаступление в некотором испытании (эксперименте) зависит от ряда случайных факторов. Примеры: успешная сдача экзамена; выигрыш в лотерее; рождения мальчика или девочки; всхожесть семян; попадание в цель и т. д.

8.2. Определение вероятности

События, образующие полную группу попарно несовместных и равновозможных событий, будем называть элементарными событиями.

Классическое определение вероятности

Вероятностью P(A) события A называется отношение числа элементарных событий m, благоприятствующих событию A, к числу всех элементарных событий n:

Вероятность достоверного события равна 1.
Вероятность невозможного события равна 0.
Вероятность случайного события больше 0 и меньше 1.

Статистическое определение вероятности

Классическое определение вероятности не является пригодным для изучения произвольных случайных событий. Например, оно неприемлемо, если результаты испытания не равновозможны. В таких случаях используется статистическое определение вероятности. Пусть проводится n опытов, событие A наступило m раз, тогда

,

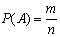
Геометрическое определение вероятности

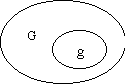
Если в результате проведения испытаний наблюдается произвольный исход из некоторого бесконечного множества, то можно сказать, что пространство элементарных исходов может быть некоторой областью G, а под событием А можно понимать исходы, входящие в область g. Пусть на область G наугад брошена «точка»; приняв равновозможность вариантов, естественно считать, что вероятность попадания в область g можно найти по формуле, называемой геометрической вероятностью:

Области могут быть различной размерности (одно-, двух- или трехмерного измерения) и, в зависимости от выбора размерности меры, могут принимать значения либо длины, либо площади, либо объема. Для конкретного испытания размерность мер g и G должна быть одна.

8.3. Свойства вероятности

Теорема. Вероятность суммы двух несовместных событий A и B равна сумме вероятностей этих событий: P (A + B) = P(A) + P(B).

Следствие. Сумма вероятностей противоположных событий А и равна единице:

Вероятность суммы полной группы событий равна 1.

Произведением событий А и В называется событие С = АВ, состоящее в том, что в результате испытания произошло и событие А и событие В.

Два события A и B называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события A и B называются зависимыми.

Чаще всего зависимые испытания происходят тогда, когда тянут из одной колоды, не возвращая карты в колоду, вытаскивают из одной урны и т. д.

Теорема. Вероятность произведения двух независимых событий A и B равна произведению их вероятностей:

Теорема. Вероятность произведения двух зависимых событий A и B равна произведению вероятности одного из них на условную вероятность другого, найденного в предположении, что первое событие уже наступило:

Теорема. Вероятность суммы двух совместных событий A и B равна сумме вероятностей этих событий минус вероятность их произведения

Теорема (формула полной вероятности). Вероятность события A, которое может наступить лишь при условии появления одного из n попарно несовместных событий B1, B2,…, Bn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A:

Вопросы

1. Может ли событие быть одновременно и невозможным и достоверным?
2. Входит ли в понятие суммы событий (А + В) событие, состоящее в одновременном наступлении события А и события В?
3. Приведите пример полной группы событий для выбранного Вами испытания.
4. Исходя из формулы определения вероятности, объясните, почему значение вероятности находится в пределах от 0 до 1.
5. Часто ли случается, что наступление какого-либо события зависит от ряда причин? Приведите пример.
6. С помощью какой формулы можно выяснить наиболее вероятную причину уже наступившего события?

Источник

Что можно сказать о вероятностях событий входящих в полную систему информатика

Данный урок хочу посвятить теме «Измерение информации».

Выделяют следующие подходы к определению количества информации :

Данные подходы изучаются в школьном курсе информатики.

Вероятностный подход

Вероятностный подход связан с таким понятием как ВЕРОЯТНОСТЬ.
ВЕРОЯТНОСТЬ — это отношение количества тех наблюдений, при которых рассматриваемое событие наступило, к общему количеству наблюдений. Такая трактовка допустима в случае достаточно большого количества наблюдений или опытов.

Единицы измерения информации: бит, байт, кбайт и т.д.

За 1 бит информации принимают такое количество информации, которое находится в сообщении о том, что произошло одно событие из двух равновероятных.

1 бит — это количество информации, уменьшающее неопределенность знаний в два раза.

При РАВНОВЕРОЯТНОСТНОМ ПОДХОДЕ вероятности наступления того или иного события равны.

Для измерения количества информации, полученной нами при равновероятном событии, используем формулу

(где N — количество возможных исходов события (2 стороны в примере с монеткой),
i — количество информации, которое мы получим, при том или ином исходе события)

Другие задачи с разбором и для самостоятельного решения на тему «Вероятностный подход к измерению информации» смотрите в следующих выпусках.

При НЕРАВНОВЕРОЯТНОСТНОМ ПОДХОДЕ вероятности исходов событий не равны.

Пример: В коробке 16 карандашей. Из них 8 синих, 4 красных, 4 зеленых. Вероятность достать из коробки синий карандаш больше, чем вероятность достать зеленый или красный.

Для измерения количества информации при неравновероятностном подходе используют следующие формулы:

(где К — количество интересующих нас событий (достать синий карандаш K=8), N — общее количество события)

(где i — количество информации, которое мы получим, при том или ином исходе события)

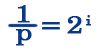
Вторая формула называется формулой Шеннона (правда в другом виде). В оригинале формула Шеннона выглядит так

Использование или неиспользовании этой формулы зависит от того, знают ли ученики про логарифм или нет.

Задача: В коробке 16 карандашей. Из них 8 синих, 4 красных, 4 зеленых. Сколько бит информации мы получим, вытащив из коробки синий карандаш?

Ответ : 1 бит информации мы получим, вытащив синий карандаш из коробки.

Продолжение рассмотрения этой темы смотрите в следующих постах.

Источник

Вероятность и информация

Презентация к уроку по теме «Вероятность и информация» в 10 классе по учебнику Семакин И.Г.

Просмотр содержимого документа
«Вероятность и информация»

Сначала разберемся с понятием «вероятность». Введем следующие понятия:

Вероятностью случайного события ( p ) называется отношение числа благоприятствующих событию исходов (m) к общему числу исходов (n):

Заметим, что вероятность случайного события может изменяться от 0 до 1.

В беспроигрышной лотерее разыгрывается 3 книги, 2 альбома, 10 наборов маркеров, 10 блокнотов.

Какова вероятность выиграть книгу?

Общее число исходов 2+3+10+10=25; число благоприятствующих исходу событий равно 3. Вероятность выигрыша книги вычисляется по формуле: p =3/25=0,12.

Заметим, что во многих случаях события происходят с разной вероятностью, а значит формула N =2 i не всегда применима.

Вероятностный подход предполагает, что возможные события имеют различные вероятности реализации.

В этом случае, зная вероятность ( p ) событий, можно определить количество информации ( i ) в сообщении о каждом из них из формулы:

I – количество информации (бит);

N – количество возможных событий;

Качественная связь между вероятностью события и количеством информации в сообщении состоит в следующем: чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии.

В корзине лежат 8 черных шаров и 24 белых. Сколько бит информации несет сообщение о том, что достали черный шар?

Решение. Общее число исходов: 8+24=32, число благоприятствующих исходу событий равно 8. Вероятность выбора черного шара определяется как p =8/32=1/4=0,25

Количество информации вычисляем из соотношения 2 i =1/0,25=4,

В корзине лежат 20 шаров. Из них 10 черных, 5 белых, 4 желтых и 1 красный. Сколько информации несет сообщение о том, что достали красный шар?

1) Найдем вероятность вытягивания шара красного цвета

2) Найдем количество информации

В непрозрачном мешочке 10 белых,

20 красных, 30 синих и 40 зеленых шариков. Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика?

1) Найдем общее количество шаров в мешочке

2) Найдем вероятность вытягивания шара

3) Найдем количество информации

I=-(0,1 · log 2 0,1+0,2 · log 2 0,2+ 0,3 · log 2 0,3+ 0,4 · log 2 0,4)=

1.В ящике лежат 36 красных и несколько зеленых яблок. Сообщение “Из ящика достали зеленое яблоко” несет 2 бита информации. Сколько яблок в ящике?

2. В концертном зале 270 девушек и несколько юношей. Сообщение “Первым из зала выйдет юноша” содержит 4 бита информации. Сколько юношей в зале.

3. В корзине 15 яблок, 15 груш и 30 слив. Сколько бит информации несет сообщение о том, что из корзины извлечена груша?

4. В коробке лежат 16 разноцветных фломастеров. Какое количество информации содержит сообщение, что из коробки достали фиолетовый фломастер?

Источник

Содержание урока

Информация и вероятность

Информация и вероятность

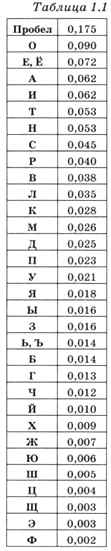
Всё, что написано в предыдущем пункте, верно только при одном уточнении: все события (символы алфавита) одинаково ожидаемы, т. е. нельзя заранее сказать, что какой-то символ встречается чаще, а какой-то — реже. В реальности это предположение не всегда верно. Например, в тексте на русском языке некоторые символы встречаются часто, а некоторые — очень редко. Числа во втором столбце табл. 1.1 означают относительную долю символа в больших текстах. Например, доля 0,175 для пробела означает, что примерно 17,5% всех символов в текстах на русском языке — пробелы.

Иногда среди всех возможных событий есть ожидаемые и неожиданные. Например, на вопрос «Идёт ли сейчас снег?» летом мы ожидаем услышать ответ «Нет». При этом ответ «Да» будет очень неожиданным, и после его получения наши дальнейшие планы могут сильно измениться. Это значит, что при таком ответе мы получаем гораздо больше информации. Как её измерить точно?

Сначала нужно разобраться с тем, что значит «менее ожидаемое» событие и «более ожидаемое». Математики в этом случае используют понятие «вероятность»: если событие более ожидаемое, то его вероятность (точнее, вероятность того, что оно произойдёт) больше.

Вероятность — это число в интервале от 0 до 1. В математике вероятность принято обозначать буквой р (от латинского probabi- lis — вероятный, возможный).

Сначала рассмотрим предельные случаи, когда вероятность равна 0 или 1. Пусть, например, х — некоторое неизвестное вещественное число, которое задумал ведущий. Вы знаете, что для любого вещественного х всегда х 2 ≥ 0. В этом случае считают, что вероятность события х₂ ≥ 0 равна 1 (событие х₂ ≥ 0 обязательно произойдёт). Часто вероятность измеряют в процентах от 1, тогда вероятность события х 2 ≥ 0 равна 100%. В то же время вероятность события х 2 2 < 0 никогда не произойдёт.

Теперь предположим, что мы бросаем монету и смотрим, какой стороной она упала, «орлом» или «решкой». Если повторять этот опыт много раз, мы заметим, что количество «орлов» и «решек» примерно равно (конечно, если монета не имеет дефектов). При этом вероятность каждого из двух событий равна 0,5, или 50%. Скорее всего, вы слышали выражение «50 на 50», которое означает, что ни одному из двух вариантов нельзя отдать предпочтение — их вероятности равны.

Вероятность события можно определить с помощью большого количества испытаний. Если из N испытаний нужное нам событие случилось m раз, то вероятность такого события можно оценить как m/N. Например, классический игральный кубик имеет 6 граней; если кубик качественный, вероятность выпадения каждой грани равна 1/6. Вероятность выпадения чётного числа можно подсчитать так: среди чисел от 1 до 6 всего 3 чётных числа, поэтому при большом числе испытаний в половине случаев (в 3 из 6) будут выпадать чётные числа, т. е. вероятность равна 0,5. А вероятность выпадения числа, меньшего 3, равна 2/6 = = 1/3 ≈ 0,33, потому что только 2 из 6 чисел (1 и 2) удовлетворяют условию.

Теперь можно переходить к главному вопросу: как вычислить количество информации, если в сообщении получен символ, вероятность появления которого равна р. Попробуем сначала определить, какими свойствами должна обладать эта величина, исходя из «здравого смысла».

Во-первых, чем меньше вероятность, тем более неожидан символ и тем больше информации мы получили. Если вероятность события близка к нулю, количество информации должно стремиться к бесконечности (получение такого символа очень неожиданно).

Во-вторых, представим себе, что мы получаем символы только одного вида, например только буквы «А». Тогда вероятность появления символа «А» равна 1 и никакой новой информации в этом символе для нас нет — мы всё заранее знали. Следовательно, при р = 1 информация должна быть равна нулю.

В-третьих, «здравый смысл» подсказывает, что когда мы бросаем игральный кубик два (три, 102, 1002) раза, мы получаем информации в два (три, 102, 1002) раза больше, чем при однократном бросании кубика. Это свойство называют принципом аддитивности (сложения).

Если событие имеет вероятность р, то количество информации в битах, полученное в сообщении об этом событии, равно

Третье свойство (аддитивность, сложение вероятностей) проверим на примере. Пусть есть два мешка, в каждом из которых лежат 8 шариков разного цвета. Вычислим, какое количество информации мы получили из сообщения «Из первого мешка вытащили (наугад) красный шарик, а из второго — зелёный». Из каждого мешка можно вытащить один из восьми шариков, т. е. вероятность вытащить какой-то определённый шарик равна 1/8. Следовательно, количество информации в сообщении «Из первого мешка вытащили красный шарик» равно

Точно такую же информацию, 3 бита, мы получаем из сообщения «Из второго мешка вытащили зелёный шарик».

Теперь посмотрим, какое количество информации несёт исходное полное сообщение «Из первого мешка вытащили (наугад) красный шарик, а из второго — зелёный». Какова вероятность именно этого исхода? Есть 8 способов вытащить шарик из каждого мешка, всего получаем 8 • 8 = 64 варианта, поэтому вероятность каждого из них равна 1/64. Тогда количество информации в сообщении равно

т. е. равно сумме количеств информации в двух отдельных сообщениях. Мы показали, что свойство аддитивности выполняется.

Возможно, вы уже заметили, что последний пример фактически свёлся к использованию формулы Хартли. Если все N вариантов имеют равные вероятности, то вероятность каждого варианта равна р = 1/N, следовательно, количество информации о любом из N возможных событий вычисляется как

Этот результат совпадает с формулой Хартли.

Однако формулу Хартли нельзя использовать, если вероятности событий разные. Пусть, например, детям раздают воздушные шарики разного цвета, причём 7 из каждых 10 шариков — зелёные. Какое количество информации содержится в сообщении «Маша получила зелёный шарик»? Здесь формула Хартли неприменима, однако можно использовать формулу (1). Вероятность того, что Маше достался зелёный шарик, равна 7/10, а количество информации вычисляется как

Величина под знаком двоичного логарифма не является степенью двойки. Как её вычислить? Для этого используется свойство логарифма, позволяющее переходить к другому основанию, например, к десятичным или натуральным логарифмам, которые умеют вычислять калькуляторы:

В данном случае получаем

Следующая страница Вопросы и задания

Cкачать материалы урока

Источник

Вероятностный подход к определению количества информации «Формула Шеннона. Применение ЭТ Excel для решения задач на нахождение количества информации»

Материал разработан на 2 спаренных урока.

Цели уроков: Сформировать у учащихся понимание вероятности, равновероятных событий и событий с различными вероятностями. Научить находить количество информации, используя вероятностный подход. Создать в Excel информационную модель для автоматизации процесса вычислений в задачах на нахождение количества информации, используя формулу Шеннона.

Требования к знаниям и умениям:

Учащиеся должны знать:

Учащиеся должны уметь:

Оборудование: доска, компьютер, мультимедийный проектор, карточки с заданиями, карточки-памятки, справочный материал.

Урок 1. Вероятностный подход к определению количества информации. Формула Шеннона

Ход урока

I. Организационный момент.

II. Проверка домашнего задания.

III. Постановка цели урока.

Задача: Какое сообщение содержит большее количество информации?

Первые три варианта учащиеся решают без затруднения. События равновероятны, поэтому можно применить для решения формулу Хартли. Но третье задание вызывает затруднение. Делаются различные предположения. Роль учителя: подвести учащихся к осмыслению, что в четвертом варианте мы сталкиваемся с ситуацией, когда события неравновероятны. Не все ситуации имеют одинаковые вероятности реализации. Существует много таких ситуаций, у которых вероятности реализации различаются. Например, если бросают несимметричную монету или «правило бутерброда».

Сегодня на уроке мы должны ответить на вопрос: как вычислить количество информации в сообщении о неравновероятном событии.

IV. Объяснение нового материала.

Для вычисления количества информации в сообщении о неравновероятном событии используют следующую формулу: I=log₂(1/p)

где I – это количество информации, р – вероятность события.

Вероятность события выражается в долях единицы и вычисляется по формуле: р=K/N,

где К – величина, показывающая сколько раз произошло интересующее нас событие, N – общее число возможных исходов какого-то процесса.

Вернемся к нашей задаче.

Пусть К₁ – это количество пирожков с повидлом, К₁=24

К₂ – количество пирожков с капустой, К₂=8

N – общее количество пирожков, N = К₁ +К₂=24+8=32

Вычислим вероятность выбора пирожка с разной начинкой и количество информации, которое при этом было получено.

Вероятность выбора пирожка с повидлом: р₁=24/32=3/4=0,75.

Вероятность выбора пирожка с капустой: р₂=8/32=1/4=0,25.

Обращаем внимание учащихся на то, что в сумме все вероятности дают 1.

Вычислим количество информации, содержащееся в сообщении, что Маша выбрала пирожок с повидлом: I₁=log₂(1/p₁)= log₂(1/0,75)= log₂1,3=1,15470 бит.

Вычислим количество информации, содержащееся в сообщении, если был выбран пирожок с капустой: I₂=log₂(1/p₂)= log₂(1/0,25)= log₂4=2 бит.

Пояснение: если учащиеся не умеют вычислять значение логарифмической функции, то можно использовать при решении задач этого урока следующие приемы:

Приложение 1. «Количество информации в сообщении об одном из N равновероятных событий: I= log₂N». (Приложение вы можете получить у автора статьи.)

При сравнении результатов вычислений получается следующая ситуация: вероятность выбора пирожка с повидлом больше, чем с капустой, а информации при этом получилось меньше. Это не случайность, а закономерность.

Качественную связь между вероятностью события и количеством информации в сообщении об этом событии можно выразить так: чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии.

Вернемся к нашей задаче с пирожками. Мы еще не ответили на вопрос: сколько получим информации при выборе пирожка любого вида?

Ответить на этот вопрос нам поможет формула вычисления количества информации для событий с различными вероятностями, которую предложил в 1948 г. американский инженер и математик К.Шеннон.

можно расписать формулу в таком виде:

Рассмотрим формулу на нашем примере:

Теперь мы с вами можем ответить на вопрос задачи, которая была поставлена в начале урока. Какое сообщение содержит большее количество информации?

Ответ: в 1 сообщении.

Обратите внимание на 3 и 4 задачу. Сравните количество информации.

Мы видим, что количество информации достигает максимального значения, если события равновероятны.

Интересно, что рассматриваемые нами формулы классической теории информации первоначально были разработаны для технических систем связи, призванных служить обмену информацией между людьми. Работа этих систем определяется законами физики т.е. законами материального мира. Задача оптимизации работы таких систем требовала, прежде всего, решить вопрос о количестве информации, передаваемой по каналам связи. Поэтому вполне естественно, что первые шаги в этом направлении сделали сотрудники Bell Telephon Companie – X. Найквист, Р. Хартли и К. Шеннон. Приведенные формулы послужили К. Шеннону основанием для исчисления пропускной способности каналов связи и энтропии источников сообщений, для улучшения методов кодирования и декодирования сообщений, для выбора помехоустойчивых кодов, а также для решения ряда других задач, связанных с оптимизацией работы технических систем связи. Совокупность этих представлений, названная К. Шенноном “математической теорией связи”, и явилась основой классической теории информации. (Дополнительный материал можно найти на сайте http://polbu.ru/korogodin_information или прочитав книгу В.И. Корогодин, В.Л. Корогодина. Информация как основа жизни. Формула Шеннона.)

Можно ли применить формулу К. Шеннона для равновероятных событий?

Мы видим, что формула Хартли является частным случаем формулы Шеннона.

V. Закрепление изучаемого материала.

Задача: В корзине лежат 32 клубка красной и черной шерсти. Среди них 4 клубка красной шерсти.

Сколько информации несет сообщение, что достали клубок красной шерсти? Сколько информации несет сообщение, что достали клубок шерсти любой окраски?

Дано: К_к=4;N=32

Найти: I_к, I

Решение:

VI. Подведение итогов урока.

Урок 2. Применение ЭТ Excel для решения задач на нахождение количества информации

Пояснение: При решении задач на нахождение количества информации учащиеся не вычисляли значение логарифма, т.к. не знакомы с логарифмической функцией. Урок строился таким образом: сначала решались однотипные задачи с составлением формул, затем разрабатывалась табличная модель в Excel, где учащиеся делали вычисления. В конце урока озвучивались ответы к задачам.

Ход урока

I. Постановка целей урока

На этом уроке мы будем решать задачи на нахождение количества информации в сообщении о неравновероятных событиях и автоматизируем процесс вычисления задач данного типа.

Для решения задач на нахождение вероятности и количества информации используем формулы, которые вывели на прошлом уроке:

р_i=K_i/N; I_i=log₂(1/p_i);

II. Решение задач.

Ученикам дается список задач, которые они должны решить.

Задачи решаются только с выводами формул, без вычислений.

В озере обитает 12500 окуней, 25000 пескарей, а карасей и щук по 6250. Какое количество информации несет сообщение о ловле рыбы каждого вида. Сколько информации мы получим, когда поймаем какую-нибудь рыбу?

Решение:

III. Объяснение нового материала.

Задается вопрос ученикам:

1. Какие трудности возникают при решении задач данного типа? (Отв.: Вычисление логарифмов).

2. Нельзя ли автоматизировать процесс решения данных задач? (Отв.: можно, т.к. алгоритм вычислений в этих задачах один и тот же).

3. Какие программы используются для автоматизации вычислительного процесса? (Отв.: ЭТ Excel).

Давайте попробуем сделать табличную модель для вычисления задач данного типа.

Нам необходимо решить вопрос, что мы будем вычислять в таблице. Если вы внимательно присмотритесь к задачам, то увидите, что в одних задачах надо вычислить только вероятность событий, в других количество информации о происходящих событиях или вообще количество информации о событии.

Мы сделаем универсальную таблицу, где достаточно занести данные задачи, а вычисление результатов будет происходить автоматически.

Структура таблицы обсуждается с учениками. Роль учителя обобщить ответы учащихся.

При составлении таблицы мы должны учитывать:

Прежде чем демонстрировать заполнение таблицы, учитель повторяет правила ввода формул, функций, операцию копирования (домашнее задание к этому уроку).

При заполнении таблицы показывает как вводить логарифмическую функцию. Для экономии времени учитель демонстрирует уже готовую таблицу, а ученикам раздает карточки-памятки по заполнению таблицы.

Рассмотрим заполнение таблицы на примере задачи №1.

Рис. 1. Режим отображения формул

Рис. 2. Отображение результатов вычислений

Результаты вычислений занести в тетрадь.

Если в решаемых задачах количество событий больше или меньше, то можно добавить или удалить строчки в таблице.

VI. Практическая работа.

1. Сделать табличную модель для вычисления количества информации.

2. Используя табличную модель, сделать вычисления к задаче №2 (рис.3), результат вычисления занести в тетрадь.

3. Используя таблицу-шаблон, решить задачи №3,4 (рис.4, рис.5), решение оформить в тетради.

4. Сохранить таблицы в своих папках под именем «инф_вероятность».

В классе 30 человек. За контрольную работу по информатике получено 15 пятерок, 6 четверок, 8 троек и 1 двойка. Какое количество информации несет сообщение о том, что Андреев получил пятерку?

В коробке лежат кубики: 10 красных, 8 зеленых, 5 желтых, 12 синих. Вычислите вероятность доставания кубика каждого цвета и количество информации, которое при этом будет получено.

В непрозрачном мешочке хранятся 10 белых, 20 красных, 30 синих и 40 зеленых шариков. Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика?

VII. Подведение итогов урока.

Учитель оценивает работу каждого ученика. Оценивается не только практическая работа на компьютере, но и оформление решения задачи в тетради.

VIII. Домашняя работа.

1. Параграф учебника «Формула Шеннона», компьютерный практикум после параграфа.

2. Доказать, что формула Хартли – частный случай формулы Шеннона.

Литература:

Источник