Что можно сделать с целыми числами
Целые числа
К целым числам относятся натуральные числа, ноль, а также числа, противоположные натуральным.
Натуральные числа — это положительные целые числа.
Латинской буквой \( \mathbb
К примеру: 1, 3, 7, 19, 23 и т.д. Такие числа мы используем для подсчета (на столе лежит 5 яблок, у машины 4 колеса и др.)
Латинской буквой \( \mathbb
К натуральным числам нельзя отнести отрицательные (у стула не может быть отрицательное количество ножек) и дробные числа (Иван не мог продать 3,5 велосипеда).
Арифметические действия с целыми числами
Что можно делать с целыми числами? Их можно перемножать, складывать и вычитать друг из друга. Разберем каждую операцию на конкретном примере.
Сложение целых чисел
Два целых числа с одинаковыми знаками складываются следующим образом: производится сложение модулей этих чисел и перед полученной суммой ставится итоговый знак:
Вычитание целых чисел
Два целых числа с разными знаками складываются следующим образом: из модуля большего числа вычитается модуль меньшего и перед полученным ответом ставят знак большего по модулю числа:
Умножение целых чисел
Чтобы умножить одно целое число на другое нужно выполнить перемножение модулей этих чисел и поставить перед полученным ответом знак «+», если исходные числа были с одинаковыми знаками, и знак «−», если исходные числа были с разными знаками:
Следует запомнить следующее правило перемножения целых чисел:
Существует правило перемножения нескольких целых чисел. Запомним его:
Знак произведения будет «+», если количество множителей с отрицательным знаком четное и «−», если количество множителей с отрицательным знаком нечетное.
\( (-5) \cdot (-4) \cdot (+1) \cdot (+6) \cdot (+1) = +120 \)
Деление целых чисел
Деление двух целых чисел производится следующим образом: модуль одного числа делят на модуль другого и если знаки чисел одинаковые, то перед полученным частным ставят знак «+», а если знаки исходных чисел разные, то ставится знак «−».
Свойства сложения и умножения целых чисел
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Целые числа
К целым числам относятся натуральные числа, ноль, а также числа, противоположные натуральным.
Натуральные числа — это положительные целые числа.
Содержание
Латинской буквой \mathbb
К примеру: 1, 3, 7, 19, 23 и т.д. Такие числа мы используем для подсчета (на столе лежит 5 яблок, у машины 4 колеса и др.)
Латинской буквой \mathbb
К натуральным числам нельзя отнести отрицательные (у стула не может быть отрицательное количество ножек) и дробные числа (Иван не мог продать 3,5 велосипеда).
Арифметические действия с целыми числами
Что можно делать с целыми числами? Их можно перемножать, складывать и вычитать друг из друга. Разберем каждую операцию на конкретном примере.
Сложение целых чисел
Два целых числа с одинаковыми знаками складываются следующим образом: производится сложение модулей этих чисел и перед полученной суммой ставится итоговый знак:
Вычитание целых чисел
Два целых числа с разными знаками складываются следующим образом: из модуля большего числа вычитается модуль меньшего и перед полученным ответом ставят знак большего по модулю числа:
Умножение целых чисел
Чтобы умножить одно целое число на другое нужно выполнить перемножение модулей этих чисел и поставить перед полученным ответом знак « + », если исходные числа были с одинаковыми знаками, и знак « − », если исходные числа были с разными знаками:
Следует запомнить следующее правило перемножения целых чисел:
Существует правило перемножения нескольких целых чисел. Запомним его:
Знак произведения будет « + », если количество множителей с отрицательным знаком четное и « − », если количество множителей с отрицательным знаком нечетное.
(-5) \cdot (-4) \cdot (+1) \cdot (+6) \cdot (+1) = +120
Деление целых чисел
Деление двух целых чисел производится следующим образом: модуль одного числа делят на модуль другого и если знаки чисел одинаковые, то перед полученным частным ставят знак « + », а если знаки исходных чисел разные, то ставится знак « − ».
Свойства сложения и умножения целых чисел
Целые числа: общее представление
В данной статье определим множество целых чисел, рассмотрим, какие целые называются положительными, а какие отрицательными. Также покажем, как целые числа используются для описания изменения некоторых величин. Начнем с определения и примеров целых чисел.
Целые числа. Определение, примеры
Определение 1. Целые числа
Целые числа и координатная прямая
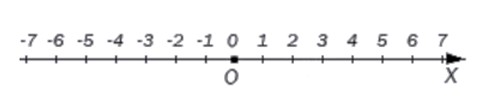
Пусть координатная прямая проведена горизонтально и направлена вправо. Взглянем на нее, чтобы наглядно представить расположение целых чисел на прямой.
В любую точку прямой, координатой которой является целое число, можно попасть, отложив от начала координат некоторое количество единичных отрезков.
Положительные и отрицательные целые числа
Из всех целых чисел логично выделить положительные и отрицательные целые числа. Дадим их определения.
Определение 2. Положительные целые числа
Определение 3. Отрицательные целые числа
Число 0 разделяет положительные и отрицательные целые числа и само не является ни положительным, ни отрицательным.
Любое число, противоположное положительному целому числу, в силу определения, является отрицательным целым числом. Справедливо и обратное. Число, обратное любому отрицательному целому числу, есть положительное целое число.
Можно дать другие формулировки определений отрицательных и положительных целых чисел, используя их сравнение с нулем.
Определение 4. Положительные целые числа
Соответственно, положительные числа лежат правее начала отсчета на координатной прямой, а отрицательные целые числа находятся левее от нуля.
Неположительные и неотрицательные целые числа
Определение 6. Неотрицательные целые числа
Как видим, число нуль не является ни положительным, ни отрицательным.
Использование целых чисел при описании изменения величин
Для чего используются целые числа? В первую очередь, с их помощью удобно описывать и определять изменение количества каких-либо предметов. Приведем пример.
Пусть на складе хранится какое-то количество коленвалов. Если на склад привезут еще 500 коленвалов, то их количество увеличится. Число 500 как раз и выражает изменение (увеличение) количества деталей. Если потом со склада увезут 200 деталей, то это число также будет характеризовать изменение количества коленвалов. На этот раз, в сторону уменьшения.
Если же со склада ничего не будут забирать, и ничего не будут привозить, то число 0 укажет на неизменность количества деталей.
Очевидное удобство использования целых чисел в отличие от натуральных в том, что их знак явно указывает на направление изменения величины (увеличение или убывание).
Числа. Целые числа. Свойства целых чисел.
Целые числа – это натуральные числа, а также противоположные им числа и нуль.
Целые числа — расширение множества натуральных чисел N, которое получается путем добавления к N 0 и отрицательных чисел типа − n. Множество целых чисел обозначают Z.
Сумма, разность и произведение целых чисел дают снова целые числа, т.е. целые числа составляют кольцо относительно операций сложения и умножения.
Целые числа на числовой оси:
Сколько целых чисел? Какое количество целых чисел? Самого большого и самого маленького целого числа нет. Этот ряд бесконечен. Наибольшее и наименьшее целое число не существует.
Натуральные числа еще называются положительными целыми числами, т.е. фраза «натуральное число» и «положительное целое число» это одно и то же.
Ни обыкновенные, ни десятичные дроби не являются целыми числами. Но существуют дроби с целыми числами.
Операции над целыми числами.
1. Сумма целых чисел.
Для сложения двух целых чисел с одинаковыми знаками, необходимо сложить модули этих чисел и перед суммой поставить итоговый знак.
2. Вычитание целых чисел.
Для сложения двух целых чисел с разными знаками, необходимо из модуля числа, которое больше вычесть модуль числа, которое меньше и перед ответом поставить знак большего числа по модулю.
3. Умножение целых чисел.
Для умножения двух целых чисел, необходимо перемножить модули этих чисел и перед произведением поставить знак плюс (+), если исходные числа были одного знака, и минус (–) – если разного.
Когда умножаются несколько чисел, знак произведения будет положительным, если число неположительных сомножителей чётное, и отрицателен, если нечётное.
(–2) ∙ (+3) ∙ (–5) ∙ (–3) ∙ (+4) = –360 (3 неположительных сомножителя).
4. Деление целых чисел.
Для деления целых чисел, необходимо поделить модуль одного на модуль другого и поставить перед результатом знак «+», если знаки чисел одинаковые, и минус, – если разные.
Свойства целых чисел.
Z не замкнуто относительно деления 2-х целых чисел (например, 1/2). Ниже приведенная таблица показывает некоторые основные свойства сложения и умножения для любых целых a, b и c.
Свод правил по работе с целыми числами в C/C++
В основу статьи легли мои собственные выработанные нелегким путем знания о принципах работы и правильном использовании целых чисел в C/C++. Помимо самих правил, я решил привести список распространенных заблуждений и сделать небольшое сравнение системы целочисленных типов в нескольких передовых языках. Все изложение строилось вокруг баланса между краткостью и полноценностью, чтобы не усложнять восприятие и при этом отчетливо передать важные детали.
Всякий раз, когда я читаю или пишу код на C/C++, мне приходится вспоминать и применять эти правила в тех или иных ситуациях, например при выборе подходящего типа для локальной переменной/элемента массива/поля структуры, при преобразовании типов, а также в любых арифметических операциях или сравнениях. Обратите внимание, что типы чисел с плавающей запятой мы затрагивать не будем, так как это большей частью относится к анализу и обработке ошибок аппроксимации, вызванных округлением. В противоположность этому, математика целых чисел лежит в основе как программирования, так и компьютерной науки в целом, и в теории вычисления здесь всегда точны (не считая проблем реализации вроде переполнения).
Типы данных
Базовые целочисленные типы
Целочисленные типы устанавливаются с помощью допустимой последовательности ключевых слов, взятых из набора
Несмотря на то, что битовая ширина каждого базового целочисленного типа определяется реализацией (т.е. зависит от компилятора и платформы), стандартом закреплены следующие их свойства:
Наличие знака
Дополнительные правила
Типы из стандартных библиотек
Преобразования
Представим, что значение исходного целочисленного типа нужно преобразовать в значение целевого целочисленного типа. Такая ситуация может возникнуть при явном приведении, неявном приведении в процессе присваивания или при продвижении типов.
Как происходит преобразование?
Главный принцип в том, что, если целевой тип может содержать значение исходного типа, то это значение семантически сохраняется.
Арифметика
Продвижение/преобразование
Неопределенное поведение
Счетчик цикла
Выбор типа
Отсчет вниз
Для циклов, ведущих отсчет вниз, более естественным будет использовать счетчик со знаком, потому что тогда можно написать:
При этом для беззнакового счетчика код будет таким:
Заблуждения
Все пункты приведенного ниже списка являются мифами. Не опирайтесь на эти ложные убеждения, если хотите писать корректный и портируемый код.