Что изучает математика свойства предметов

Математика

Содержание

Основные сведения

Идеализированные свойства исследуемых объектов либо формулируются в виде аксиом, либо перечисляются в определении соответствующих математических объектов. Затем по строгим правилам логического вывода из этих свойств выводятся другие истинные свойства (теоремы). Эта теория в совокупности образует математическую модель исследуемого объекта. Таким образом первоначально, исходя из пространственных и количественных соотношений, математика получает более абстрактные соотношения, изучение которых также является предметом современной математики.

Традиционно математика делится на теоретическую, выполняющую углублённый анализ внутриматематических структур, и прикладную, предоставляющую свои модели другим наукам и инженерным дисциплинам, причём некоторые из них занимают пограничное с математикой положение. В частности, формальная логика может рассматриваться и как часть философских наук, и как часть математических наук; механика — и физика, и математика; информатика, компьютерные технологии и алгоритмика относятся как к инженерии, так и к математическим наукам и т. д. В литературе было предложено много различных определений математики (см. ниже).

Этимология

В текстах на русском языке слово «математика» или «мафематика» встречается по крайней мере с XVII века, например, у Николая Спафария в «Книге избранной вкратце о девяти мусах и о седмих свободных художествах» (1672 год) [5]

Определения

Одно из первых определений предмета математики дал Декарт [6] :

К области математики относятся только те науки, в которых рассматривается либо порядок, либо мера и совершенно не существенно, будут ли это числа, фигуры, звёзды, звуки или что-нибудь другое, в чём отыскивается эта мера. Таким образом, должна существовать некая общая наука, объясняющая всё относящееся к порядку и мере, не входя в исследование никаких частных предметов, и эта наука должна называться не иностранным, но старым, уже вошедшим в употребление именем Всеобщей математики.

Математика… наука о количественных отношениях и пространственных формах действительного мира.

Это определение Энгельса [8] ; правда, далее Колмогоров поясняет, что все использованные термины надо понимать в самом расширенном и абстрактном смысле.

Сущность математики… представляется теперь как учение об отношениях между объектами, о которых ничего не известно, кроме описывающих их некоторых свойств,— именно тех, которые в качестве аксиом положены в основание теории… Математика есть набор абстрактных форм — математических структур.

Приведём ещё несколько современных определений.

Герман Вейль пессимистически оценил возможность дать общепринятое определение предмета математики:

Вопрос об основаниях математики и о том, что представляет собой в конечном счёте математика, остаётся открытым. Мы не знаем какого-то направления, которое позволит в конце концов найти окончательный ответ на этот вопрос, и можно ли вообще ожидать, что подобный «окончательный» ответ будет когда-нибудь получен и признан всеми математиками.

Разделы математики

1. Математика как учебная дисциплина подразделяется в Российской Федерации на элементарную математику, изучаемую в средней школе и образованную дисциплинами:

и высшую математику, изучаемую на нематематических специальностях вузов. Дисциплины, входящие в состав высшей математики, варьируются в зависимости от специальности.

Программа обучения по специальности математика [13] образована следующими учебными дисциплинами:

2. Математика как специальность научных работников Министерством образования и науки Российской Федерации [14] подразделяется на специальности:

3. Для систематизации научных работ используется раздел «Математика» [15] универсальной десятичной классификации (УДК).

4. Американское математическое общество (AMS) выработало свой стандарт для классификации разделов математики. Он называется Mathematics Subject Classification. Этот стандарт периодически обновляется. Текущая версия — это MSC 2010. Предыдущая версия — MSC 2000.

Обозначения

Вследствие того, что математика работает с чрезвычайно разнообразными и довольно сложными структурами, система обозначений также очень сложна. Современная система записи формул сформировалась на основе европейской алгебраической традиции, а также математического анализа (понятия функции, производной и т. д.). Геометрия испокон века пользовалась наглядным (геометрическим же) представлением. В современной математике распространены также сложные графические системы записи (например, коммутативные диаграммы), нередко также применяются обозначения на основе графов.

Краткая история

Академиком А. Н. Колмогоровым предложена такая структура истории математики:

Развитие математики началось вместе с тем, как человек стал использовать абстракции сколько-нибудь высокого уровня. Простая абстракция — числа; осмысление того, что два яблока и два апельсина, несмотря на все их различия, имеют что-то общее, а именно занимают обе руки одного человека, — качественное достижение мышления человека. Кроме того, что древние люди узнали, как считать конкретные объекты, они также поняли, как вычислять и абстрактные количества, такие, как время: дни, сезоны, года. Из элементарного счёта естественным образом начала развиваться арифметика: сложение, вычитание, умножение и деление чисел.

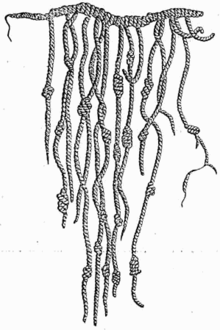
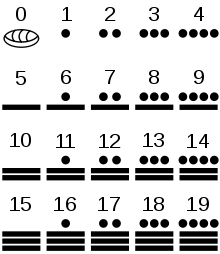
Развитие математики опирается на письменность и умение записывать числа. Наверно, древние люди сначала выражали количество путём рисования чёрточек на земле или выцарапывали их на древесине. Древние инки, не имея иной системы письменности, представляли и сохраняли числовые данные, используя сложную систему верёвочных узлов, так называемые кипу. Существовало множество различных систем счисления. Первые известные записи чисел были найдены в папирусе Ахмеса, созданном египтянами Среднего царства. Индская цивилизация разработала современную десятичную систему счисления, включающую концепцию нуля.

Исторически основные математические дисциплины появились под воздействием необходимости вести расчёты в коммерческой сфере, при измерении земель и для предсказания астрономических явлений и, позже, для решения новых физических задач. Каждая из этих сфер играет большую роль в широком развитии математики, заключающемся в изучении структур, пространств и изменений.

Философия математики

Цели и методы

Математика изучает воображаемые, идеальные объекты и соотношения между ними, используя формальный язык. В общем случае математические понятия и теоремы не обязательно имеют соответствие чему-либо в физическом мире. Главная задача прикладного раздела математики — создать математическую модель, достаточно адекватную исследуемому реальному объекту. Задача математика-теоретика — обеспечить достаточный набор удобных средств для достижения этой цели.

Содержание математики можно определить как систему математических моделей и инструментов для их создания. Модель объекта учитывает не все его черты, а только самые необходимые для целей изучения (идеализированные). Например, изучая физические свойства апельсина, мы можем абстрагироваться от его цвета и вкуса и представить его (пусть не идеально точно) шаром. Если же нам надо понять, сколько апельсинов получится, если мы сложим вместе два и три, — то можно абстрагироваться и от формы, оставив у модели только одну характеристику — количество. Абстракция и установление связей между объектами в самом общем виде — одно из главных направлений математического творчества.

Другое направление, наряду с абстрагированием — обобщение. Например, обобщая понятие «пространство» до пространства n-измерений. «Пространство , при 3″ border=»0″ /> является математической выдумкой. Впрочем, весьма гениальной выдумкой, которая помогает математически разбираться в сложных явлениях». [16]

Изучение внутриматематических объектов, как правило, происходит при помощи аксиоматического метода: сначала для исследуемых объектов формулируются список основных понятий и аксиом, а затем из аксиом с помощью правил вывода получают содержательные теоремы, в совокупности образующие математическую модель.

Основания

Вопрос сущности и оснований математики обсуждался со времён Платона. Начиная с XX века наблюдается сравнительное согласие в вопросе, что надлежит считать строгим математическим доказательством, однако отсутствует согласие в понимании того, что в математике считать изначально истинным. Отсюда вытекают разногласия как в вопросах аксиоматики и взаимосвязи отраслей математики, так и в выборе логических систем, которыми следует при доказательствах пользоваться.

Помимо скептического, известны нижеперечисленные подходы к данному вопросу.

Теоретико-множественный подход

Предлагается рассматривать все математические объекты в рамках теории множеств, чаще всего с аксиоматикой Цермело — Френкеля (хотя существует множество других, равносильных ей). Данный подход считается с середины XX века преобладающим, однако в действительности большинство математических работ не ставят задач перевести свои утверждения строго на язык теории множеств, а оперируют понятиями и фактами, установленными в некоторых областях математики. Таким образом, если в теории множеств будет обнаружено противоречие, это не повлечёт за собой обесценивание большинства результатов.

Логицизм

Данный подход предполагает строгую типизацию математических объектов. Многие парадоксы, избегаемые в теории множеств лишь путём специальных уловок, оказываются невозможными в принципе.

Формализм

Данный подход предполагает изучение формальных систем на основе классической логики.

Интуиционизм

Интуиционизм предполагает в основании математики интуиционистскую логику, более ограниченную в средствах доказательства (но, как считается, и более надёжную). Интуиционизм отвергает доказательство от противного, многие неконструктивные доказательства становятся невозможными, а многие проблемы теории множеств — бессмысленными (неформализуемыми).

Конструктивная математика

Основные темы

Числа

Понятие «число» первоначально относилось к натуральным числам. В дальнейшем оно было постепенно распространено на целые, рациональные, действительные, комплексные и другие числа.

Натуральные числа Целые числа Рациональные числа Вещественные числа
Комплексные числа	Кватернионы

Числовые системы
Счётные множества	Натуральные числа () • Целые () • Рациональные () • Алгебраические () • Периоды • Вычислимые • Арифметические
Вещественные числа и их расширения	Вещественные () • Комплексные () • Кватернионы () • Числа Кэли (октавы, октонионы) () • Седенионы () • Альтернионы • Процедура Кэли — Диксона • Дуальные • Гиперкомплексные • Суперреальные • Гиперреальные • Surreal number (англ.)
Другие числовые системы	Кардинальные числа • Порядковые числа (трансфинитные, ординал) • p-адические • Супернатуральные числа
См. также	Двойные числа • Иррациональные числа • Трансцендентные • Числовой луч • Бикватернион

Преобразования

Арифметика	Дифференциальное и интегральное исчисление	Векторный анализ	Анализ
Дифференциальные уравнения	Динамические системы	Теория хаоса

Структуры

Пространственные отношения

Более наглядные подходы в математике.

Дискретная математика

Дискретная математика включает средства, которые применяются над объектами, способными принимать только отдельные, не непрерывные значения.

Математическая логика	Теория вычислимости	Криптография	Теория графов

Коды в системах классификации знаний

Онлайновые сервисы

Существует большое число сайтов, предоставляющих сервис для математических расчётов. Большинство из них англоязычные. [20] Из русскоязычных можно отметить сервис математических запросов поисковой системы Nigma.

Источник

Конспект урока математики 1 класс

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Урок 1

Тема: «Что изучает математика».

1) сформировать представления о свойствах предметов (цвет, форма, размер, материал, количество и т.д.), и выделить из них те, которые изучаются на уроках математики;

2) сформировать представление об учебнике математики, способность к самоопределению (на примере самоопределения к учебной деятельности на уроке математики);

3) тренировать навык работы с таблицами (строка, столбец), навык описания свойств предметов и определения предмета по его свойствам.

Мыслительные операции, необходимые на этапе проектирования: анализ, сравнение, обобщение, аналогия.

1) фотография учеников класса на экскурсии;

3) картинки с обозначением 2 шагов учебной деятельности:

4) изображение белочки:

6) портрет автора учебника (Л.Г. Петерсон);

7) текст с поздравлением от автора;

8) текст с заданием для пробного действия;

9) увеличенный вариант картинки к заданию № 1 , стр. 1;

10) прозрачные полоски;

11) поэтапно заполняемый эталон свойств предметов:

12) заготовки букв П, Ф, Р, К;

13) наборы разноцветных кругов;

14) модели шара, цилиндра, куба и параллелепипеда;

15) нарисованная на доске таблица 4  4.

1) наборы разноцветных кругов;

2) предметы формы шара, цилиндра, параллелепипеда и куба;

3) таблица 4  4 с обозначениями свойств предметов для этапа первичного закрепления;

4) таблица 4  4 и картинки с обозначениями свойств предметов.

1. Мотивация к учебной деятельности.

1) мотивировать учащихся к учебной деятельности (экскурсия до урока, фотографии);

2) определить содержательные рамки урока.

Организация учебного процесса на этапе 1:

Один из предшествующих уроков был посвящен знакомству учащихся со структурой учебной деятельности. На данном уроке были зафиксированы 2 шага учебной деятельности. Также заранее учитель организует экскурсию по школе: «В гости к старшеклассникам». В ходе ее дети знакомятся с разными чудесами, которые умеют делать старшеклассники, например: а) в кабинете химии две белых жидкости сливаются в один сосуд, и получается красная жидкость; б) в кабинете физики луч света превращается в радугу и т.д. Важно, чтобы они эмоционально пережили удивление, восхищение, желание научиться делать так же. Желательно, чтобы во время экскурсии были сделаны фотографии или слайды.

Недавно вы познакомились с тем, что делают ученики на различных уроках. Что вам больше всего запомнилось?

Ученики рассказывают, о том, что они запомнили из прошлой экскурсии. Учитель предлагает фотографии, на которых зафиксированы наиболее яркие эпизоды экскурсии.

Что делали на уроках ученики? (Они проводили опыты, читали, решали задачи, работали за компьютерами…)

Зачем они это делали? (Чтобы узнать что-то новое, научиться, …)

А вы чем будете заниматься на уроке? (Учиться, узнавать новое.)

Что значит учиться? (Значит сделать два шага: понять чего мы не знаем, самим открыть новое знание.)

Учитель открывает два шага учебной деятельности Д-3.

На сегодняшнем уроке мы начнем (или продолжим) разговор о том, чему вы будете учиться на уроке математики.

2. Актуализация знаний и фиксация затруднения в пробном действии.

1) актуализировать представления об уроке как форме организации учебного процесса в школе, о различных учебных дисциплинах, о назначении учебников;

2) актуализировать представления о свойствах предметов — цвет, форма, размер, материал, зафиксировать их в виде символов;

3) тренировать навык работы с таблицами (строка, столбец), навык описания свойств предметов и определения предмета по его свойствам;

4) зафиксировать индивидуальное затруднение.

Организация учебного процесса на этапе 2:

Сегодня к нам на урок пришел гость. А кто это, отгадайте:

По деревьям скачет

И орешки прячет? (Белочка.)

А может, это все-таки лисичка? Почему? (Нет, лисичка не может скакать по деревьям, она не ест орехи.)

Молодцы! Вы, верно, узнали белочку по описанию ее свойств.

Учитель вешает на доску рисунок белочки, достает два конверта.

Ребята! Сегодня у вас необычный день – вы пришли на первый в вашей жизни урок математики! Белочка поздравляет вас с этим событием и хочет пожелать, чтобы изучение математики было для Вас интересным! В подарок она передает два конверта. В одном из них лежит телеграмма от автора вашего учебника!

Дети хлопают в ладоши. Учитель продолжает беседу.

Она нужна людям, чтобы понимать и преобразовывать окружающий мир. Помощником в нашей работе по этому предмету будет учебник математики, который написала Людмила Георгиевна Петерсон.

Учитель показывает ученикам учебник и демонстрирует фотографию автора.

Давайте прочитаем телеграмму: «Дорогие первоклассники! Поздравляю вас с вашим первым уроком математики! На этом уроке вы научитесь считать, проводить измерения, решать задачи и примеры. Поможет вам освоить математику — учебник. В нем вы найдете много интересных заданий, выполняя которые вы будете открывать для себя удивительный мир математики. Если задачи покажутся вам сложными, постарайтесь решить их вместе с одноклассниками или обратитесь за помощью к учителю. Ведь нет ничего, что не могли бы преодолеть верные друзья! Итак, открывайте свой учебник, и в добрый путь! Мы желаем Вам успеха!».

Учитель демонстрирует учебник и открывает его на произвольной странице.

Откройте учебник математики. Обратите внимание, какой он красочный. В каждой картинке прячется задание.

Учитель демонстрирует учебник на первой странице.

Откройте первую страницу и посмотрите на первую картинку. Расскажите, что на ней изображено?

Ученики по очереди рассказывают о предметах изображенных на картинке.

Теперь я предлагаю вам задание, которое спряталось в этой картинке. Оказывается это не простая картинка, а картинка-игра.

Я вам буду рассказывать о предмете, изображенном на этой картинке, а вы находите этот предмет, показываете его пальчиком и называете этот предмет. Начинаем игру. Красный, посуда. (Ученики показывают пальцем на чашку, и называют: «чашка».)

Молодцы! Зеленый, предназначен для еды (Ученики показывают на огурец, и называют его.)

Молодцы! А как вам удалось найти предметы, которые я загадала? (По свойствам, описанию и т.д., которые вы называли.)

Вспомните, какие свойства предметов я называла? (Цвет, назначение — для чего этот предмет используется.)

Цвет, назначение предмета называют его свойствами. Попробуйте загадать свойства предмета, изображенного на этой картинке, а мы постараемся найти его. Не забудьте, что в загадке используется цвет и назначение предмета.

Ученики составляют аналогичные загадки и разгадывают их.

Как бы вы назвали задание к этой картинке? (Ученики придумывают названия.)

Автор учебника обещала, что, выполняя задания, мы будем узнавать что-то новое. Что нового мы узнали при выполнении этого задания? (Что предметы имеют свойства; предмет можно найти по его свойствам; цвет и назначение являются свойствами предметов; по картинкам учебника можно придумывать задания.)

Учитель открывает часть доски, на которой находится незаполненный эталон, и прикрепляет обозначения цвета и назначения. Эталон принимает вид:

Теперь к этой картинке я придумаю другое задание. Я называю место, на котором расположен предмет, а вы называете этот предмет. Предмет расположен на второй строке во втором столбце.

Учитель прозрачными полосками показывает вторую строку и второй столбец, ученики называют огурец.

Предмет расположен на третьей строке в первом столбце. (Кастрюля.)

Учитель предлагает ученикам составить аналогичные задания. После того как разгаданы 2–3 загадки, учитель задает вопрос:

Что нового вы узнали при выполнении этого задания? (Предмет можно определить по его положению. К одной картинке можно придумать несколько заданий.)

Значит, расположение предмета является его свойством.

Учитель подходит к доске, на которой находится незаполненный эталон, и прикрепляет обозначение расположения. Эталон принимает вид:

Расскажите, что вы видите на следующей картинке? (Круги разного цвета.)

Учитель выставляет на доске на «липучке» или магнитах такие же круги.

На ваших столах лежат конверты с такими же кругами. Часть кругов я откладываю, и вы отложите такие же круги.

Учитель отклеивает желтые и красные круги и перевешивает их в сторону. Ученики откладывают такие же круги в отдельную группу.

Назовите свойство, по которому я выбирала круги в эту часть. (Большие круги.)

Назовите общее свойство кругов в оставшейся части. (Маленькие круги.)

Чем отличаются круги в этих двух группах? (Размером.)

Таким образом, выполняя это упражнение, мы узнали, что размер — это свойство, по которому можно сравнивать предмеры. Придумайте пары предметов, один из которых маленький, а другой большой. (Ответы детей.)

Учитель подходит к доске, на которой находится незаполненный эталон, и прикрепляет обозначение размера. Эталон принимает вид:

Теперь к этой же картинке я предлагаю новое задание. Возьмите простой карандаш и зачеркните круги в группе, где их больше всего. (Ученики зачеркивают пять синих кругов.)

Обведите группу, в которой три круга. (Ученики обводят зеленые круги.)

В какой группе кругов меньше всего? (В группе, содержащий один маленький круг.)

По какому свойству мы сравнивали группы кругов (Много их или мало, сколько предметов в группе, …) Это свойство называется количеством предметов. Его используют для сравнения групп предметов.

Учитель прикрепляет к эталону обозначение количества. Эталон принимает вид:

Белочка показывает игру: «Счет через 2». Разбившись парами и стоя лицом друг к другу, дети считают до 10, поочередно хлопая в ладоши и касаясь ладонями друг друга: хлопнуть в ладоши (1), коснуться ладонями друг друга (2), хлопнуть в ладоши (3), коснуться ладонями друг друга (4) и т.д. Задача – добиться дружного, синхронного счета и выполнения движений.

В завершение, в благодарность белочке дети могут попрыгать, имитируя ее движения.

Учитель берет в руки модель шара:

Обратите внимание на следующую картинку. Назовите предметы на этой картинке, которые похожи на этот… (Шар. Это кувшин, мяч, глобус, самовар.)

Назовите, чем отличается мяч от глобуса. (Цветом, расположением на картинке, назначением.)

А что у них общего? (Они расположены на первой строке, оба похожи на шар.)

О предметах, похожих на шар, говорят, что они имеют форму шара. Возьмите в руки шар. Приведите примеры предметов формы шара.

Далее учитель берет в руки цилиндр:

Кто знает название этой модели?

Если ученики отвечают «цилиндр», то педагог их поощряет — «молодцы!». Если они молчат или отвечают неправильно, то учитель сам дает название модели.

Я держу в руках цилиндр. Возьмите в руки цилиндр. Назовите на этой картинке предметы, которые имеют форму цилиндра. (Стакан, ведерко, карандаши, коробка.)

Аналогично, демонстрируются прямоугольный параллелепипед (коробка) и куб.

Чем куб отличается от параллелепипеда? (Куб не удлиненный, а параллелепипед удлиненный.)

Какие предметы на второй картинке имеют форму параллелепипеда? (Аквариум, коробка для кубиков, коробка для карандашей, коробка для чая.)

Какие из них имеют форму куба? (Коробка для чая, кубики.)

Значит, есть предметы, которые имеют форму круга, шара, цилиндра, параллелепипеда. Как назвать новое свойство предметов, которое мы узнали? (Форма предметов.)

Учитель подходит к доске, на которой находится незаполненный эталон, и прикрепляет обозначение формы. Эталон принимает вид:

Далее учитель показывает на эталоне обозначения свойств, а дети называют их.

А теперь, назовите свойства, с которыми мы с вами познакомились. (Цвет, назначение, положение, размер, количество, форма.)

Как вы думаете, почему мы с этого начали урок? (Это нам поможет, пригодиться.)

Какое задание будет следующее? (Задание, с помощью которого мы узнаем новое.)

Для этого белочка приготовила второй конверт. Готовы узнать, какое задание в нем? (Да.)

Учитель открывает конверт и читает задание.

Какие свойства изучает математика?

Учащиеся самостоятельно пытаются определить свойства.

Учащиеся, не выполнившие задание, поднимают руку. Учитель фиксирует, что дети не смогли выполнить задание.

У кого есть ответы?

Учащиеся перечисляют свои варианты.

Кто из вас может доказать, что он прав? (Молчание.)

Учитель фиксирует, что дети не могут обосновать свой ответ.

3. Выявление места и причины затруднения.

выявить и зафиксировать место и причину затруднения.

Организация учебного процесса на этапе 3:

Какое задание вы выполняли? (Мы должны были выделить свойства, которые изучает математика.)

Где возникло затруднение? Что не получилось? (Некоторые из учащихся не могут определить изучается свойство в математике или нет, некоторые не могут доказать свое мнение.)

Почему возникло затруднение? (Мы только начали изучать математику, мы не знаем, что изучается на уроке математики.)

4. Построение проекта выхода из затруднения.

1) согласовать и зафиксировать цель и тему урока;

2) построить план и определить средства достижения цели.

Организация учебного процесса на этапе 4:

Так что мы должны сделать на уроке? (Узнать, что изучает математика, и выделить нужные свойства.)

Поэтому наш первый урок называется «Что изучает математика?».

Что же нам поможет? Чем вы пользовались, когда узнавали свойства предметов? (Учебником.)

Учебник точно знает ответ на этот вопрос. Именно в нем рассказывается о свойствах, которые изучаются на уроке математики. Как же он нам поможет? (Давайте полистаем его и ответим на вопрос.)

А как вы это сделаете, если вы еще не умеет читать? (По картинкам.)

Что мы сделаем с выделенными свойствами? (Мы их обозначим.)

5. Реализация построенного проекта.

1) организовать коммутативное взаимодействие с целью реализации построенного проекта, направленного на приобретение недостающих знаний;

2) организовать фиксацию построенного способа действия в речи и знаково (с помощью эталона);

3) организовать уточнение общего характера нового знания.

Организация учебного процесса на этапе 5:

Итак, переверните первую страницу. Перед вами фигуры различной формы. Значит, какое свойство предметов изучается на уроке математики? (Форма.)

Переверните еще две страницы (урок 4). На этих картинках вы видите большие и маленькие предметы. Какие свойства изучает математика? (Размеры предметов.)

А здесь фея обращает наше внимание на таблицу. О каком свойстве она хочет нам напомнить? (Положение предметов.)

Если ученики затрудняются ответить на этот вопрос, им можно указать на значок положения предметов на эталоне.

А количество предметов изучается в математике? (Да.)

Здесь все единодушны. Учитель в ходе беседы ставит на эталоне рядом со знаками формы, размера, расположения и количества предметов соответственно буквы Ф, Р, П, К. Затем указкой показывает их на эталоне и просит учеников назвать хором свойства, которые изучаются в математике.

Удалось нам справиться с возникшим затруднением? (Да.)

6. Первичное закрепление.

зафиксировать свойства предметов, которые изучаются на уроках математики, во внешней речи.

Организация учебного процесса на этапе 5:

Можем ли мы завершить этот урок? (Нет.)

Почему? (Надо еще потренироваться, закрепить новые знания.)

1) – Вернемся на первую страницу учебника. Белочка с удивлением рассматривает первую картинку и думает: «А на урок математики ли я попала?» Почему так удивлена белочка? (Свойства, по которым собраны предметы — размер и назначение — не изучаются на уроке математики.)

Вы совершенно правы. А какие свойства изучаются на этом уроке? (Форма, размер, количество, положение предметов.)

Назовите эти свойства друг другу в парах.

2) На столах у детей таблица, в клетках которой нарисованы обозначения свойств:

Источник