Что изучает математическая логика

Логика математическая

Математическая логика — это раздел современной формальной логики (см. Логика формальная), в котором логические выводы исследуются посредством логических исчислений на основе математического языка, аксиоматизации и формализации. В качестве другого названия современного этапа в развитии логики (см. Логика) используется также термин «символическая логика» (см. Логика символическая). Иногда термин «математическая логика» употребляется в более широком смысле, охватывая исследование свойств дедуктивных теорий, именуемое металогикой (см. Металогика) или метаматематикой. В целом, определение «математическая логика» подчёркивает её сходство с математикой, основывающееся, прежде всего, на методах построения логических исчислений на основе строгого символического языка, аксиоматизации и формализации. Они позволяют избежать двусмысленной и логической неясности естественного языка, которым пользовалась при описании правильного мышления традиционная логика, развивавшаяся в рамках философии (см. Философия).

Математические методы дали логике такие преимущества, как высокая точность формулировок, возможность изучения более сложных, с точки зрения логической формы, объектов. Многие проблемы, исследуемые в математической логике, вообще невозможно было сформулировать с использованием только традиционных методов. Применение в логике математических методов становится возможным тогда, когда суждения формулируются на некотором точном (формализованном) языке. Такие точные языки имеют две составляющие: синтаксис (см. Синтактика) и семантику (см. Семантика). Синтаксисом называется совокупность правил построения объектов языка (обычно называемых формулами). Семантикой называется совокупность соглашений, описывающих наше понимание формул (или некоторых из них) и позволяющих считать одни формулы верными, а другие — нет.

Уже в Античности (в частности Аристотелем) широко применялись буквенные обозначения для переменных. Идея построения универсального языка для всей математики, для формализации на базе такого языка математических доказательств и вообще любых рассуждений выдвигалась в XVII веке Г. В. Лейбницем. Но только к середине XIX века стало очевидным, что существующая логическая парадигма, а именно аристотелевская силлогистика (см. Силлогистика), уже не отвечает требованиям развития науки того времени. С одной стороны, значительные успехи абстрактной алгебры в особенности в теории групп позволили перенести алгебраические методы на другие области науки. Это с успехом проделала английская школа, основоположником которой можно считать А. де Моргана, который в 1847 году опубликовал книгу «Formal Logic; or The Calculus of Inference, Necessary and Probable». Им открыты названные в его честь законы де Моргана, разработана теория отношений и в 1838 определено понятие математической индукции.

Однако наибольшую известность получили работы Дж. Буля. В 1847 году он публикует брошюру «Mathematical Analaysis of Logic», а в 1854 — свой главный труд по логике «An Investigation into the Laws of Thought, on which are Founded the Mathematical Theories of Logic and Probabilities». Как и де Морган, Дж. Буль был одним из тех математиков из Кембриджа, которые признали чисто абстрактную природу алгебры. Они заметили, что простейшие операции над множествами подчиняются законам коммутативности, ассоциативности и дистрибутивности. Оставалось только провести аналогию между объединением и сложением, пересечением и умножением, пустым классом и нулём, универсальным классом и единицей. Работы Буля 1847 и 1854 годов можно считать началом алгебры логики (см. Алгебра логики), первоначальный этап развития которой был завершён Э. Шрёдером в трёхтомной монографии «Vorlesungugen uber die Algebra der Logik» (1890–1905).

С другой стороны, возникновение и развитие математической логики связано с работами Г. Фреге и Ч. С. Пирса. После того, как Фреге в 1879 и Пирс в 1885 году ввели в язык алгебры логики предикаты, предметные переменные и кванторы, возникла реальная возможность построения системы логики в виде логического исчисления, что и было сделано Фреге, который по праву считается основателем математической логики в её современном понимании. Пытаясь реализовать идеи Лейбница, Фреге в своём труде «Begriffsschrift» предложил символическую запись для строгих рассуждений. Хотя его нотация сейчас совсем не используется (например, формулы рисовали в виде двумерного дерева), Фреге в действительности впервые построил исчисление предикатов. Исчисление предикатов есть формальная система, состоящая из двух частей: символического языка и логики предикатов (см. Логика предикатов). Кроме этого для исчисления предикатов Фреге даёт строгое определение понятия «доказательство», которое является общепринятым и по сей день.

Основы современной логической символики были разработаны Дж. Пеано, чьи интересы, как и Фреге, концентрировались вокруг оснований математики и развития формально-логического языка. Его широко известный труд «Formulaire de mathématiques», опубликованный (в соавторстве) в годах, был нацелен на развитие математики в её целостности, исходя из некоторых фундаментальных постулатов. Логическая запись Пеано была принята, хотя и частично модифицирована, А. Н. Уайтхедом и Б. Расселом в их широко известной трёхтомной «Principia Mathematica» (1910–1913), а затем воспринята Д. Гилбертом. Таким образом, в логику был введён символический язык. Создание такого искусственного языка и с его помощью таких объектов, как логические исчисления, строго формализующие различные теории в виде некоторого конечного списка аксиом и правил вывода, было вызвано, в первую очередь, потребностями математики, ставившей проблемы, для решения которых средства традиционной логики были непригодны.

Основным стимулом развития математической логики в начале XX века была проблема оснований математики. К. Вейерштрасс, Р. Дедекинд и Г. Кантор показали, что в качестве фундамента всей классической математики может рассматриваться арифметика целых чисел. Дедикинд и Пеано аксиоматизировали арифметику, а Фреге дал определение натурального числа как множества всех равномощных множеств. Таким образом, вся математика сводилась к теории множеств. Рефлексия над феноменом множеств привела к обнаружению ряда парадоксов в теории множеств, ответом на которые стало развитие четырёх направлений в основаниях математики:

Развитие и применение технического аппарата самой логики в первую очередь относится к программе Д. Гилберта (начиная с 1904 года), где была поставлена главная задача: найти строгое основание для математики посредством доказательства её непротиворечивости, то есть доказательства того факта, что в ней недоказуема никакая формула вида A вместе с формулой

А. Для этого потребовалось развить теорию доказательств, после чего, считал Гилберт, используя только финитные методы, можно будет доказать непротиворечивость теории множеств и самой теории действительных чисел и таким образом решить проблему оснований математики. Однако результат К. Гёделя о неполноте арифметики (1931) убедительно показал, что программа Гилберта невыполнима. Теорема Гёделя о неполноте утверждает, что всякая достаточно богатая теория необходимо содержит утверждения, которые нельзя ни доказать, ни опровергнуть, не опровергнув самой теории.

С годов XX века начинается современный этап развития математической логики. Он связан с применением точных методов при изучении формальных аксиоматических задач. Суть их состоит в описании рассматриваемой теории на базе строгого логико-математического языка (формализация), с последующими процедурами логического анализа теории, а именно с точки зрения непротиворечивости (например, таких теорий, как элементарная геометрия, арифметика, анализ достаточно надёжных оснований) и полноты. Основным объектом современной математической логики являются исчисления. В качестве их компонентов выступают: язык (формальный); аксиомы; правила вывода. На их основе стало возможным дать точное определение доказательства, получить точные утверждения о невозможности доказательства тех или иных предложений теории.

Обширным полем деятельности для современной математической логики является теория рекурсии, которая в первую очередь имеет дело с проблемой разрешимости: доказуема или нет формула A из некоторого множества посылок. Эти исследования привели к теориям вычислимости, к созданию компьютерных программ автоматического поиска доказательств. Решение проблемы разрешимости послужило основным стимулом для создания теории алгоритмов. Формулировка тезиса Чёрча — Тьюринга, утверждающего, что понятие общерекурсивной функции является уточнением интуитивного понятия алгоритма, стало наиболее важным достижением математической логики. Только после уточнения понятия алгоритма выяснилось, что в хорошо известных разделах математики существуют алгоритмически неразрешимые проблемы.

Важное место в современной математической логике занимает теория моделей (см. Теория моделей), которая изучает фундаментальные связи между синтаксическими свойствами множеств предложений формального языка, с одной стороны, и семантическими свойствами их моделей, с другой; и вообще, изучаются соотношения между моделями и теориями, а также преобразование моделей. Зачастую модели используются как инструмент для того, чтобы показать, что некоторая формула A не может быть дедуцирована из определённого множества постулатов или, если A есть аксиома, то показать недоказуемость A из остальных аксиом системы, к которой A принадлежит (если это возможно). Тогда A является независимой аксиомой.

Наряду с этим стало очевидно, что те впечатляющие результаты, которые были получены средствами математической логики, и в первую очередь в области оснований математики, привели к некоторому гипостазированию функции и предмета самой этой логики. Так, в предисловии к «Handbook of Mathematical Logic» (1977) Дж. Барвайс пишет: «Математическая логика традиционно подразделяется на четыре раздела: теория моделей, теория множеств, теория рекурсии и теория доказательств». В свою очередь в «Encyclopedia Britanica» (CD–1998), уже применительно к математической логике, четыре указанных раздела названы «четырьмя главными областями исследования». Более точно было бы говорить о применении технического аппарата логики в данных областях, поскольку теория множеств и теория рекурсии сами по себе являются самостоятельными математическими дисциплинами и не являются частью математической логики. Теория доказательств для некоторых математиков-логиков превратилась чуть ли не в «метаматематику» (термин Гилберта), а теория моделей давно вышла за пределы логической семантики.

Развитие современной логики показывает, что термин «математическая логика» постепенно сужается и часто используется для обозначения области исследования тех типов рассуждений, которыми пользуются математики, тем самым приобретая всё большее методологическое и прикладное значение, прежде всего в рамках вычислительной математики и связанных областей. В целом, символизация и представление различных логических теорий в виде исчислений стало обычным делом и поэтому строго разделить современные логические исследования на относящиеся к математической логике и не относящиеся к ней порой просто невозможно.

Источник

Математическая логика: происхождение, что изучает, виды

Содержание:

Хорошо известно, что в математике нет двусмысленностей. Учитывая математический аргумент, он либо действителен, либо просто нет. Оно не может быть ложным и истинным одновременно.

Особый аспект математики состоит в том, что у нее есть формальный и строгий язык, с помощью которого можно определить обоснованность аргумента. Что делает определенное рассуждение или любое математическое доказательство неопровержимым? Вот в чем суть математической логики.

Для этого используются аксиомы и другие математические аспекты, которые будут развиты позже.

Происхождение и история

Точные даты по многим аспектам математической логики неизвестны. Тем не менее, большинство библиографий по этому вопросу ведет свое происхождение от Древней Греции.

Аристотель

Начало строгого подхода к логике отчасти приписывается Аристотелю, который написал ряд логических работ, которые позднее были собраны и разработаны различными философами и учеными вплоть до Средневековья. Это можно считать «старой логикой».

Позже, в так называемую современную эпоху, Лейбниц, движимый глубоким желанием создать универсальный язык для математического мышления, и другие математики, такие как Готлоб Фреге и Джузеппе Пеано, оказали заметное влияние на развитие математической логики. Среди них аксиомы Пеано, которые формулируют необходимые свойства натуральных чисел.

Математики Джордж Буль и Георг Кантор также оказали большое влияние в то время, внося важный вклад в теорию множеств и таблицы истинности, в которых они выделяются среди других аспектов, булевой алгеброй (Джорджа Буля) и аксиомы выбора. (Джордж Кантор).

Есть также Август Де Морган с хорошо известными законами Моргана, которые рассматривают отрицания, союзы, дизъюнкции и условные выражения между предложениями, ключи к развитию символической логики, и Джон Венн со знаменитыми диаграммами Венна.

В 20 веке, примерно между 1910 и 1913 годами, Бертран Рассел и Альфред Норт Уайтхед выделяются своей публикацией Principia mathematica, набор книг, которые собирают, развивают и постулируют серию аксиом и результатов логики.

Что изучает математическая логика?

Предложения

Ниже приведены примеры выражений, которые не являются предложениями:

В первом предложении не указано, кто «она», поэтому ничего нельзя сказать. Во втором предложении не уточняется, что означает «x». Если бы вместо этого было сказано, что 2x = 6 для некоторого натурального числа x, в этом случае это соответствовало бы утверждению, фактически истинному, поскольку для x = 3 оно истинно.

Последние два утверждения не соответствуют утверждению, поскольку их невозможно отрицать или подтверждать.

Два или более предложений можно объединить (или связать) с помощью знакомых логических связок (или соединителей). Это:

Утверждения, сделанные с помощью предложений, обычно длинные, поэтому всегда утомительно писать их, как мы уже видели. По этой причине используется символический язык. Предложения обычно обозначаются заглавными буквами, например P, Q, R, S, так далее. И следующие символические связки:

В взаимный условного предложения

И встречный (или противоположный) предложения

Таблицы истинности

Значение истинности составного предложения зависит исключительно от значений истинности простых предложений, которые в нем появляются.

Чтобы работать в более общем плане, мы не будем рассматривать конкретные предложения, а будем рассматривать пропозициональные переменные. р, д, г, си т. д., которые будут представлять любые предложения.

С помощью этих переменных и логических связок формируются хорошо известные пропозициональные формулы, точно так же, как строятся сложные высказывания.

Если каждая из переменных, которые появляются в формуле высказывания, заменяется предложением, получается составное предложение.

Ниже приведены таблицы истинности логических связок:

Существуют пропозициональные формулы, которые получают только значение V в своей таблице истинности, то есть последний столбец их таблицы истинности имеет только значение V. Эти типы формул известны как тавтологии. Например:

Ниже приводится таблица истинности формулы

Говорят, что из формулы α логически следует другая формула β, если α истинно каждый раз, когда β истинно. То есть, в таблице истинности α и β строки, где α имеет V, β также имеют V. Это интересуют только строки, в которых α имеет значение V. Обозначения для логической импликации следующие. :

В следующей таблице приведены свойства логической импликации:

Две пропозициональные формулы называются логически эквивалентными, если их таблицы истинности идентичны. Для выражения логической эквивалентности используются следующие обозначения:

В следующих таблицах обобщены свойства логической эквивалентности:

Типы математической логики

Существуют разные типы логики, особенно если принять во внимание прагматическую или неформальную логику, указывающую, среди прочего, на философию.

Что касается математики, типы логики можно резюмировать следующим образом:

Области

Среди областей, в которых математическая логика незаменима при разработке своих рассуждений и аргументов, выделяются философия, теория множеств, теория чисел, алгебраическая конструктивная математика и языки программирования.

Ссылки

85 замечательных фраз и выражений на баскском языке (и их значения)

Проэритробласт: характеристика, морфология, регуляция, окраска

Источник

Знания за пределами математики и доказательной логики состоят из предположений. Предположения, составляющие математические знания, закрепляются доказательными рассуждениями и подкрепляются правдоподобными рассуждениями. Математическое доказательство является доказательным рассуждением, косвенные улики юриста, индуктивные доводы физика, статистические доводы экономиста относятся к правдоподобным рассуждениям. Доказательное рассуждение надежно, неоспоримо, окончательно. Правдоподобное рассуждение рискованно, спорно, условно.

Доказательное рассуждение имеет жесткие стандарты, кодифицированные и выясненные логикой, являющейся теорией доказательных рассуждений. Стандарты правдоподобных рассуждений текучи и нет никакой теории таких рассуждений, которая могла бы сравниться с доказательной логикой или обладала бы сравнимой с ней согласованностью.

Доказательные рассуждения. Все новые знания о мире связаны с правдоподобными рассуждениями.

Часто математические утверждения касаются бесконечного множества объектов, и перебрать эти объекты невозможно. Такой перебор можно заменить следующим методом рассуждения: если данное утверждение истинно в одном случае, то оно окажется истинным и в следующем за ним случае, а значит и во всех случаях. Такой метод рассуждения называется методом математической индукции.

Обобщение есть переход от рассмотрения данного множества предметов к рассмотрению большего множества, содержащего данное. Обобщение часто делается при переходе от одного предмета к целому классу, содержащему этот предмет.

Специализация есть переход от рассмотрения данного множества предметов к рассмотрению меньшего множества, содержащегося в данном. Специализация часто производится при переходе от целого класса предметов к одному предмету, содержащемуся в этом классе.

Аналогия. Две системы аналогичны, если они согласуются в ясно определенных отношениях соответствующих частей. Это отношение имеет ясный смысл, если отношения управляются одними и теми же законами.

Далее приводятся некоторые основные факты математической логики, которую еще называют формальной логикой. Формальной потому, что она позволяет проверить правильность рассуждений независимо от их содержания. Цепочки рассуждений в совершенно разных областях математики и других наук можно одинаково описать на языке логики и убедиться в их справедливости или ошибочности.

Высказывания и логические связки

Многие математические понятия удобно записывать в виде выражений, содержащих некоторые логические символы. Так, символ V, называемый квантором общности, используется вместо слов: «для любого», «для всех», «каково бы ни было. » и т.д., а символ

Отрицание — это высказывание, которое получается из данного высказывания А с помощью слова «не». Отрицание можно обозначать по-разному: .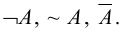

Простое добавление слова «не» к высказыванию чаще всего будет противоречить языковым нормам. Поэтому в конкретных случаях

требуется «перевод» полученного высказывания на русский язык. Пусть, например, А = «Завтра пойдет дождь». Что значит «Не (Завтра пойдет дождь)»: «Дождь пойдет не завтра», «Завтра пойдет не дождь» или «Завтра не пойдет дождь»? Здравый смысл подсказывает, что отрицанием высказывания А является третье предложение. Чтобы определить точно, дадим формальное определение отрицания.

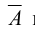
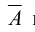
Отрицанием высказывания А называется такое высказывание, которое принимает значение / (ложно), если высказывание А истинно, и значение t (истинно), если высказывание А ложно. В нашем примере этому условию удовлетворяет только третье предложение. Итак, = «Завтра не пойдет дождь».

Дизъюнкция строится с помощью неисключающего «или». Таким образом, дизъюнкция A v В истинна, когда истинно, по крайней мере, одно из высказываний А и В или оба вместе. Другими словами, дизъюнкция ложна в том и только в том случае, когда оба высказывания ложны.

Импликация образуется из высказываний А и В с помощью слов «если. то. ». Получается высказывание вида «если А то В». Напомним, что математическая логика носит формальный характер, содержанием высказываний она не, занимается.

На примере импликации хорошо видна разница между обычным языком и языком логики. В обычном языке сложное предложение «если А, то В» предполагает между А и В отношение посылки и следствия, или же причины и обусловленного ею действия.

Импликация обозначается 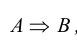, при этом говорят: «А влечет В» или «В при условии, что А», «В, если А», «А есть достаточное условие для В», «В есть необходимое условие для А».

Договорились, что импликация 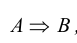ложна в том и только в том случае, когда высказывание А истинно, а высказывание В ложно. Такое определение подсказано здравым смыслом: разумно считать импликацию истинной, если В истинно, независимо от значения А; если оба участника импликации ложны, импликация, естественно, также истинна. В единственном случае, когда «предпосылка» импликации истинна, а «вывод» ложен, импликация считается ложной.

Эквиваленция образуется из высказываний А и В с помощью слов «. тогда и только тогда, когда. »:

Утверждение «А тогда и только тогда, когда В» не означает в логике, что составляющие высказывания А и В имеют одно и то же значение или один и тот же смысл.

Эквиваленция обозначается , Синонимы для эквиваленции: «если А, то В, и если В, то А», «А в том и только в том случае, когда «И есть необходимое и достаточное условие для В», «В есть необходимое и достаточное условие для А». Разумное определение эквиваленции: эквиваленция истинна в том и только в том случае, когда высказывания А и В имеют одинаковое значение истинности (либо оба истинны, либо оба ложны).

Новые высказывания (отрицание, дизъюнкция, конъюнкция, импликация и эквиваленция) образуются из существующих высказываний с помощью операций, или логических связок, имеющих те же названия.

В логике, как и в арифметике, операции делятся по старшинству. Это позволяет при записи сложных высказываний избегать большого количества скобок. Порядок выполнения операций таков: приоритет имеет отрицание, затем на одном уровне — дизъюнкция и конъюнкция, следующая связка — импликация и, наконец, самая последняя — эквиваленция.

Лекции по предметам:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник